
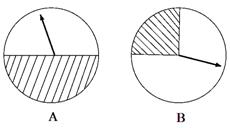
8. (石景山·理·题16)
如图,两个圆形转盘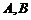 ,每个转盘阴影部分各占转盘面积的
,每个转盘阴影部分各占转盘面积的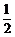 和
和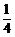 .某“幸运转盘积分活动”规定,当指针指到
.某“幸运转盘积分活动”规定,当指针指到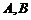 转盘阴影部分时,分别赢得积分
转盘阴影部分时,分别赢得积分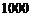 分和
分和 分.先转哪个转盘由参与者选择,若第一次赢得积分,可继续转另一个转盘,此时活动结束;若第一次未赢得积分,则终止活动.
分.先转哪个转盘由参与者选择,若第一次赢得积分,可继续转另一个转盘,此时活动结束;若第一次未赢得积分,则终止活动.
⑴记先转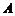 转盘最终所得积分为随机变量
转盘最终所得积分为随机变量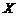 ,则
,则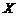 的取值分别是多少?
的取值分别是多少?
⑵如果你参加此活动,为了赢得更多的积分,你将选择先转哪个转盘?请说明理由.
[解析]
⑴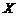 的取值分别是:0分,1000分,3000分.
的取值分别是:0分,1000分,3000分.
⑵由已知得,转动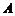 盘得到积分的概率为
盘得到积分的概率为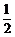 ,转动
,转动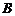 盘得到积分的概率为
盘得到积分的概率为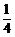 .
.
设先转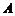 盘所得的积分为
盘所得的积分为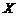 分,先转
分,先转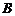 盘所得的积分为
盘所得的积分为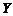 分.则有
分.则有
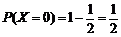 ,
,
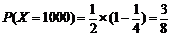 ,
,
 .
.
∴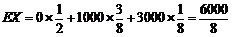 .
.
同理: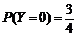 ,
,
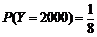 ,
,
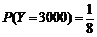 .
.
∴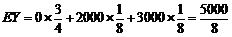 .
.
故先转 盘时,赢得积分平均水平较高.
盘时,赢得积分平均水平较高.
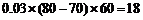 .
.
7. (海淀·文·题16)
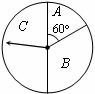
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费每满 元可以转动如图所示的圆盘一次,其中
元可以转动如图所示的圆盘一次,其中 为圆心,且标有
为圆心,且标有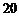 元、
元、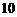 元、
元、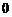 元的三部分区域面积相等. 假定指针停在任一位置都是等可能的.当指针停在某区域时,返相应金额的优惠券.(例如:某顾客消费了
元的三部分区域面积相等. 假定指针停在任一位置都是等可能的.当指针停在某区域时,返相应金额的优惠券.(例如:某顾客消费了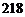 元,第一次转动获得了
元,第一次转动获得了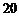 元,第二次获得了
元,第二次获得了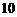 元,则其共获得了
元,则其共获得了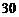 元
元 优惠券.)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
优惠券.)顾客甲和乙都到商场进行了消费,并按照规则参与了活动.
⑴若顾客甲消费了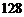 元,求他获得优惠券面额大于
元,求他获得优惠券面额大于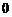 元的概率?
元的概率?
⑵若顾客乙消费了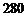 元,求他总共获得优惠券金额不低于
元,求他总共获得优惠券金额不低于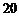 元的概率?
元的概率?
[解析]
⑴设“甲获得优惠券”为事件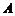
因为假定指针停在任一位置都是等可能的,而题中所给的三部分的面积相等,
所以指针停在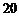 元,
元,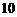 元,
元,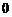 元区域内的概率都是
元区域内的概率都是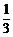 .
.
顾客甲获得优惠券,是指指针停在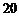 元或
元或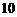 元区域,
元区域,
根据互斥事件的概率,有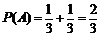 ,
,
所以,顾客甲获得优惠券面额大于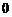 元的概率是
元的概率是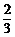 .
.
⑵设“乙获得优惠券金额不低于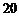 元”为事件
元”为事件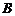
因为顾客乙转动了转盘两次,设乙第一次转动转盘获得优惠券金额为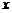 元,第二次获得优惠券金额为
元,第二次获得优惠券金额为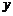 元,则基本事件空间
元,则基本事件空间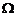 可以表示为:
可以表示为:
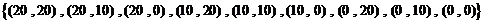 ,
,
即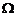 中含有
中含有 个基本事件,每个基本事件发生的概率为
个基本事件,每个基本事件发生的概率为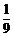 .
.
而乙获得优惠券金额不低于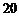 元,是指
元,是指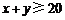 ,
,
所以事件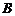 中包含的基本事件有
中包含的基本事件有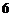 个,
个,
所以乙获得优惠券额不低于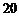 元的概率为
元的概率为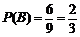
答:甲获得优惠券面额大于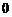 元的概率为
元的概率为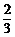 ,乙获得优惠券金额不低于
,乙获得优惠券金额不低于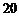 元的概率为
元的概率为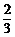 .
.
6. (海淀·理·题16)
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满 元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.
若指针停在
元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置.
若指针停在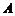 区域返券
区域返券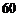 元;停在
元;停在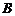 区域返券
区域返券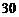 元;停在
元;停在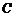 区域不返券. 例如:消费
区域不返券. 例如:消费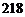 元,可转动转盘
元,可转动转盘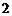 次,所获得的返券金额是两次金额之和.
次,所获得的返券金额是两次金额之和.
⑴若某位顾客消费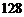 元,求返券金额不低于
元,求返券金额不低于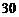 元的概率;
元的概率;
⑵若某位顾客恰好消费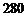 元,并按规则参与了活动,他获得返券的金额记为
元,并按规则参与了活动,他获得返券的金额记为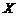 (元).求随机变量
(元).求随机变量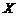 的分布列和数学期望.
的分布列和数学期望.
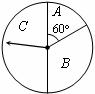
[解析]
设指针落在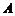 、
、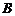 、
、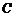 区域分别记为事件
区域分别记为事件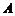 、
、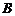 、
、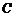 .
.
则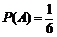 ,
,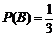 ,
,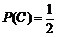 .
.
⑴ 若返券金额不低于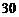 元,则指针落在
元,则指针落在 或
或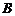 区域.
区域.
∵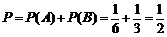
即消费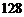 元的顾客,返券金额不低于
元的顾客,返券金额不低于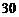 元的概率是
元的概率是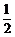 .
.
⑵ 由题意得,该顾客可转动转盘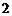 次.
次.
随机变量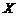 的可能值为
的可能值为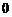 ,
,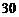 ,
,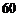 ,
, ,
,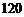 .
.
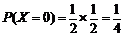 ;
;
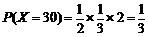 ;
;
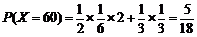 ;
;
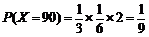 ;
;
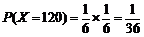 ;
;
所以,随机变量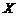 的分布列为:
的分布列为:
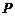 |
0 |
30 |
60 |
90 |
120 |
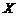 |
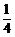 |
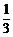 |
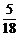 |
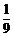 |
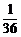 |
其数学期望 .
.
5. (西城·文·题15)
一个盒子中装有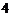 张卡
张卡 片,每张卡片上写有
片,每张卡片上写有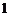 个数字,数字分别是
个数字,数字分别是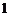 、
、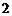 、
、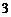 、
、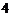 .现从盒子中随机抽取卡片.
.现从盒子中随机抽取卡片.
⑴若一次抽取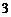 张卡片,求
张卡片,求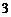 张卡片上数字之和大于
张卡片上数字之和大于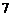 的概率;
的概率;
⑵若第一次抽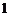 张卡片,放回后再抽取
张卡片,放回后再抽取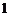 张卡片,求两次抽取中至少一次抽到数字
张卡片,求两次抽取中至少一次抽到数字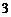 的概率.
的概率.
[解析]
⑴设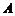 表示事件“抽取
表示事件“抽取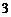 张卡片上的数字之和大于
张卡片上的数字之和大于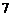 ”,
”,
任取三张卡片,三张卡片上的数字全部可能的结果是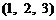 ,
, ,
,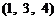 ,
,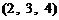 .
.
其中数字之和大于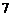 的是
的是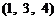 ,
,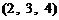 ,
,
所以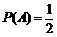 .
.
⑵设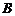 表示事件“至少一次抽到
表示事件“至少一次抽到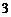 ”,
”,
第一次抽1张,放回后再抽取一张卡片的基本结果有: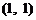
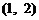
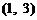
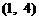
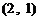
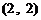
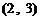
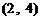
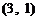
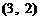

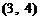
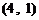
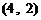
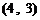
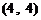 ,共
,共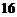 个基本结果.
个基本结果.
事件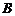 包含的基本结果有
包含的基本结果有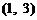
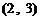
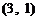
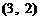

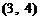
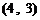 ,共
,共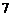 个基本结果.
个基本结果.
所以所求事件的概率为 .
.
4. (西城·文·题10)
在边长为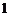 的正方形
的正方形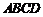 内任取一点
内任取一点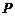 ,则点
,则点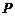 到点
到点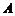 的距离小于
的距离小于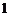 的概率为 .
的概率为 .
[解析]
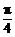 ;
;
当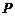 点在阴影内部时,满足到点
点在阴影内部时,满足到点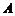 的距离小于
的距离小于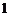 ,概率满足几何概型,故所求的概率为面积比
,概率满足几何概型,故所求的概率为面积比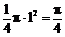 .
.
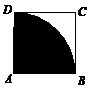
3. (东城·理·题6)(东城·文·题6)
某人向一个半径为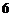 的圆形标靶射击,假设他每次射击必定会中靶,且射中靶内各点是随机的,则此人射击中靶点与靶心的距离小于
的圆形标靶射击,假设他每次射击必定会中靶,且射中靶内各点是随机的,则此人射击中靶点与靶心的距离小于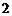 的概率为( )
的概率为( )
A.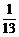 B.
B.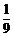 C.
C.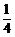 D.
D.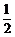
[解析] B;
满足几何概型,概率为面积比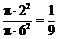 .
.
2. (朝阳·理·题5)
在区间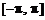 内随机取两个数分别记为
内随机取两个数分别记为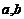 ,则使得函数
,则使得函数 有零点的概率为( )
有零点的概率为( )
A.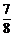 B.
B.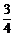 C.
C.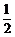 D.
D.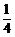
[解析] B;
若使函数有零点,必须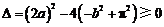 ,即
,即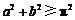 .
.
在坐标轴上将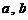 的取值范围标出,有如图所示
的取值范围标出,有如图所示
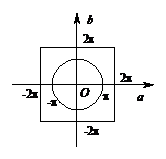
当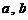 满足函数有零点时,坐标位于正方形内圆外的部分.于是概率为
满足函数有零点时,坐标位于正方形内圆外的部分.于是概率为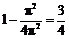 .
.
1. (朝阳·文·题5)
一只小蜜蜂在一个棱长为30的正方体玻璃容器内随机飞行. 若蜜蜂在飞行过程中与正方体玻璃容器6个表面中至少有一个的距离不大于10,则就有可能撞到玻璃上而不安全;若始终保持与正方体玻璃容器6个表面的距离均大于10,则飞行是安全的,假设蜜蜂在正方体玻璃容器内飞行到每一位置可能性相同,那么蜜蜂飞行是安全的概率是( )
A.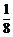 B.
B.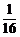 C.
C.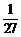 D.
D.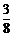
[解析] C;
容易知道,当蜜蜂在边长为10,各棱平行于玻璃容器的棱的正方体内飞行时是安全的.于是安全飞行的概率为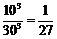 .
.
39、2005年-2009年我国某市城乡居民人均收入情况
|
指标 |
2005 |
2006 |
2007 |
2008 |
2009 |
|
城镇居民人均可支配收入(元) |
9 422 |
10 493 |
11759 |
13786 |
15781 |
|
农村居民人均纯收入(元) |
2 936 |
3 255 |
3587 |
4140 |
4761 |
|
城镇居民家庭恩格尔系数(%) |
37.7 |
36.7 |
35.8 |
36.3 |
37.9 |
|
农村居民家庭恩格尔系数(%) |
47.2 |
45.5 |
43.0 |
43.1 |
43.7 |
注:2009年某市农村居民人均纯收入4761元,扣除价格因素,比上年实际增长8.0%,城镇居民人均可支配收入15781元,扣除价格因素后实际增长8.4%。按年均纯收入1196元的标准,年末农村低收入人口为4 007万人。
统计数据显示,2008年以来居民消费价格比上年上涨4.8%,食品价格上涨12.3%。其中粮食价格上涨6.3%,肉禽及其制品价格上涨31.7%,油脂价格上升26.7%,鲜蛋价格上涨了22.9%。其中肉禽及其制品、油脂、鲜蛋价格均涨幅超过城乡居民收入增长。
(5)材料反映了什么经济现象?(10分)
2010年1月31日,新世纪以来指导“三农”工作的第7个中央一号文件由新华社受权发布。这个题为《中共中央、国务院关于加大统筹城乡发展力度,进一步夯实农业农村发展基础的若干意见》的文件推出了一系列含金量高的强农惠农新政策,强力推动资源要素向农村配置是其最大亮点。
(6)请你为“推动资源要素向农村配置”出谋划策。(10分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com