
25.(本题满分14分,第(1)小题满分5分,第(2)小题满分5分,第(3)小题满分4分)
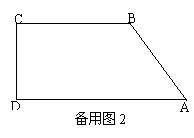
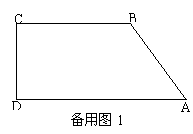
如图10,在直角梯形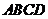 中,
中,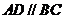 ,
,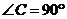 ,
,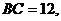
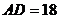 ,
,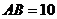 .动点
.动点 、
、 分别从点
分别从点 、
、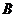 同时出发,动点
同时出发,动点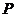 沿射线
沿射线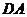 的方向以每秒2个单位长的速度运动,动点
的方向以每秒2个单位长的速度运动,动点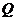 在线段
在线段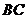 上以每秒1个单位长的速度向点
上以每秒1个单位长的速度向点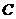 运动,当点
运动,当点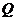 运动到点
运动到点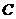 时,点
时,点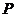 随之停止运动.设运动的时间为
随之停止运动.设运动的时间为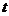 (秒).
(秒).
(1)当点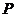 在线段
在线段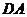 上运动时,联结
上运动时,联结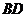 ,若
,若 =
=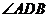 ,求
,求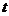 的值;
的值;
(2)当点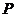 在线段
在线段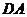 上运动时,若以
上运动时,若以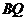 为直径的圆与以
为直径的圆与以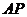 为直径的圆外切,求
为直径的圆外切,求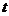 的值;
的值;
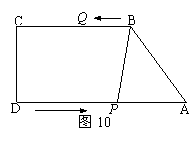 (3)设射线
(3)设射线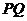 与射线
与射线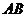 相交于点
相交于点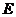 ,
,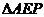 能否为等腰三角形?如果能,请直接写出
能否为等腰三角形?如果能,请直接写出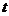 的值;如果不能,请说明理由.
的值;如果不能,请说明理由.
2010年虹口区中考数学模拟练习卷
答案要点与评分标准
说明:
24.(本题满分12分,第(1)小题满分5分,第(2)小题满分4分,第(3)小题满分3分)
已知等腰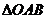 在平面直角坐标系中的位置如图9,点
在平面直角坐标系中的位置如图9,点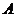 坐标为
坐标为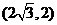 ,点
,点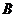 坐标为
坐标为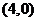 .
.
(1)若将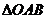 沿
沿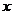 轴向左平移
轴向左平移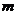 个单位,此时点
个单位,此时点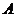 恰好落在反比例函数
恰好落在反比例函数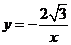 的图像上,求
的图像上,求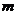 的值;
的值;
 (2)若将
(2)若将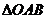 绕点
绕点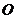 顺时针旋转
顺时针旋转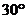 ,点
,点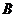 恰好落在反比例函数
恰好落在反比例函数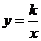 的图像上,求
的图像上,求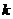 的值;
的值;
(3)若将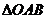 绕点
绕点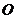 顺时针旋转
顺时针旋转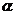 度(0<a<180)到
度(0<a<180)到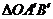 位置,当点
位置,当点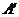 、
、 恰好同时落在(2)中所确定的反比例函数的图像上时,请直接写出经过点
恰好同时落在(2)中所确定的反比例函数的图像上时,请直接写出经过点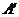 、
、 且以
且以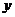 轴为对称轴的抛物线解析式.
轴为对称轴的抛物线解析式.
23.(本题满分12分,第(1)小题满分7分,第(2)小题满分3分,第(3)小题满分2分)
如图6-8中,点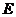 、
、 分别是正三角形
分别是正三角形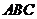 、正四边形
、正四边形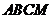 、正五边形
、正五边形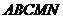 中以
中以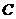 点为顶点的一边延长线和另一边反向延长线上的点,且
点为顶点的一边延长线和另一边反向延长线上的点,且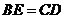 ,
,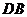 延长线交
延长线交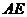 于点
于点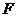 .
.
(1)求图6中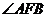 度数,并证明
度数,并证明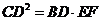 ;
;
(2)图7中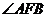 的度数为 ▲ ,图8中
的度数为 ▲ ,图8中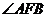 度数为 ▲ ,在图7、图8中,(1)中的等式 ▲ ;(填“成立”或“不成立”,不必证明)
度数为 ▲ ,在图7、图8中,(1)中的等式 ▲ ;(填“成立”或“不成立”,不必证明)
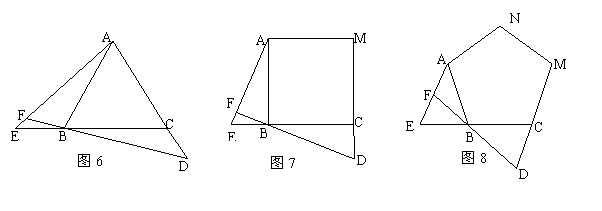 (3)若将条件“正三角形、正四边形、正五边形”改为“正
(3)若将条件“正三角形、正四边形、正五边形”改为“正 边形”,其它条件不变,则
边形”,其它条件不变,则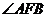 度数为 ▲ .(可用含
度数为 ▲ .(可用含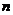 的代数式表示,不必证明)
的代数式表示,不必证明)
22.(本题满分10分,第(1)小题满分3分,第(2)小题满分2分,第(3)小题满分3分,第(4)小题满分2分)
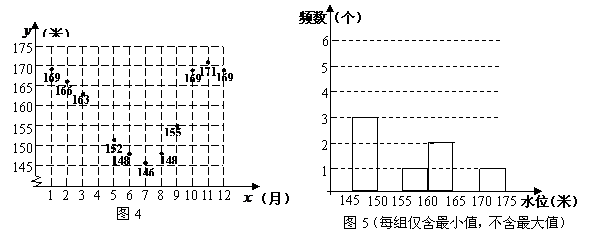
下表1是三峡水库2009年1-12月平均水位情况.小杰根据表1中的数据,在平面直角坐标系中以月份(月)为横坐标、月平均水位(米)为纵坐标描出了部分点(如图4),并绘制了不完整的频数分布直方图(如图5).请根据表1与图4、5中提供的信息,回答下列问题:
表1
月份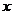 (月) (月) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
平均水位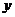 (米) (米) |
169 |
166 |
163 |
160] |
152 |
148 |
146 |
148 |
155 |
169 |
171 |
169 |
(1)根据表1,补全图4、图5;
(2)根据图4,可知平均水位相比其上个月平均水位上升最大的月份是 ▲ 月;
(3)在2009年三峡水库1-12月各月的平均水位中,众数是 ▲ 米,中位数是
▲ 米;
(4)观察图4中1-4月这些点的发展趋势,猜想1-4月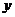 与
与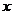 之间可以存在怎样的函数关系,请你用所学过的函数知识直接写出该函数关系式(不要求写定义域).
之间可以存在怎样的函数关系,请你用所学过的函数知识直接写出该函数关系式(不要求写定义域).
21.(本题满分10分,第(1)小题满分6分,第(2)小题满分4分)
 如图3,在菱形
如图3,在菱形 中,
中, ,过点
,过点 作
作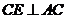 且与
且与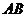 的延长线交于点
的延长线交于点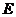 .
.
(1)求证:四边形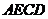 是等腰梯形;
是等腰梯形;
(2)若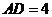 ,求梯形
,求梯形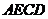 的面积.
的面积.
20.(本题满分10分)
解方程: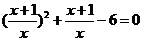 .
.
19.(本题满分10分)
先化简,再求值: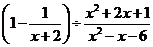 ,其中
,其中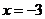 .
.
18. 已知平行四边形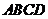 中,点
中,点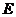 是
是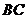 的中点,在直线
的中点,在直线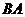 上截取
上截取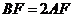 ,
,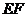 交
交
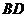 于点
于点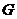 ,则
,则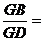 ▲ .
▲ .
17. 如图2,把矩形纸条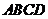 沿
沿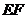 、
、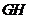 同时折叠,
同时折叠,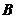 、
、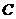 两点恰好落在
两点恰好落在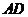 边的
边的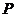 点处,若
点处,若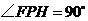 ,
,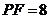 ,
,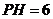 ,则矩形
,则矩形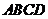 的边
的边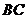 长为 ▲ .
长为 ▲ .

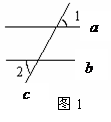
16. 如果两个相似三角形的面积比是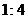 ,那么它们对应的角平分线比是 ▲ .
,那么它们对应的角平分线比是 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com