
2、 写出适合下列条件的椭圆的标准方程:
两个焦点的坐标分别是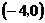 、
、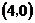 ,椭圆上一点到两焦点距离的和等于10;
,椭圆上一点到两焦点距离的和等于10;
变式一:将上题焦点改为(0,-4)、(0,4), 结果如何?
变式二:将上题改为两个焦点的距离为8,椭圆上一点P到两焦点的距离和等于10,结果如何?
1、下列方程哪些表示的是椭圆,如果是,判断它的焦点在哪个坐标轴上?


4.化简.
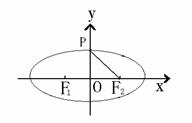
思考:观察右图,能从中找出表示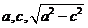 的线段吗?
的线段吗?
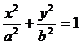 .(
.(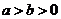 )
)
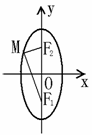 此即为椭圆的标准方程.它所表示的椭圆的焦点在
此即为椭圆的标准方程.它所表示的椭圆的焦点在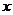 轴上,焦点是
轴上,焦点是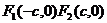 ,中心在坐标原点的椭圆方程.
,中心在坐标原点的椭圆方程.
★问三:如果椭圆的焦点F1,F2在y轴上,线段F1F2的垂直平分线为x轴,a,b,c意义同上,椭圆的方程形式又如何?
注意理解以下几点:
① 在椭圆的两种标准方程中,都有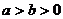 的要求;
的要求;
② 在椭圆的两种标准方程中,由于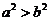 ,所以可以根据分母的大小来判定焦点在哪一个坐标轴上;
,所以可以根据分母的大小来判定焦点在哪一个坐标轴上;
③ 椭圆的三个参数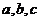 之间的关系是
之间的关系是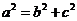 ,其中
,其中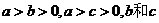 大小不确定.
大小不确定.
3.列式.
2.设点.
归纳求曲线方程的一般步骤:
建系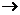 设点
设点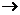 列出方程
列出方程 化简方程.
化简方程.
建系一般应遵循简单、优化的原则.
★问二 : 怎样建立坐标系,才能使求出的椭圆方程最为简单?
推导过程:
1.建系.
学生实验:按课本上介绍的方法,学生用一块纸板,两个图钉,一根无弹性的细绳尝试画椭圆.
椭圆的定义:
平面内与两个定点F1,F2的距离之和等于常数(大于| F1F2|)的点的轨迹叫作椭圆,这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距
找定义的关键处:
①平面曲线;
②任意一点到两个定点的距离的和等于常数;
③常数大于| F1F2|.
首先用多媒体演示“神州七号”飞船绕地球旋转运行的画面,并描绘出运行轨迹图.
★问一 : “神州七号”飞船绕地球旋转的轨迹是什么图形?
22. (本题满分13分)如图,在直三棱柱
(本题满分13分)如图,在直三棱柱 中,
中,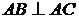 ,且
,且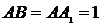


 w_w w. k#s5_
w_w w. k#s5_
(1) 求证: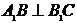
(2) 求点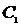 到平面
到平面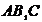 的距离;w_w
w.k_s5_
的距离;w_w
w.k_s5_
(3)设二面角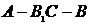 的大小为
的大小为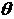 ,求
,求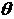 的取值范围.
的取值范围.
成都七中2009-2010学年度下期高中二年级
21、(本题满分13分)一只袋子装有大小相同的2个红球和8个黄球,从中随机连取三个球,每次取一个。记“恰有一红球”为事件A,“第三个球是红球”为事件B,求在下列情况下A、B的概率。

 w_w w. k#s5_
w_w w. k#s5_
(1)取后不放回; (2)取后放回.w_w w.k_s5_
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com