
2、利用算法的思想和方法解决实际问题,能写出一此简单问题的算法
1、算法概念和算法的基本思想
(1)算法与一般意义上具体问题的解法的联系与区别;(2)算法的五个特征。
算法作为一个名词,在中学教科书中并没有出现过,我们在基础教育阶段还没有接触算法概念。但是我们却从小学就开始接触算法,熟悉许多问题的算法。如,做四则运算要先乘除后加减,从里往外脱括弧,竖式笔算等都是算法,至于乘法口诀、珠算口诀更是算法的具体体现。广义地说,算法就是做某一件事的步骤或程序。菜谱是做菜肴的算法,洗衣机的使用说明书是操作洗衣机的算法,歌谱是一首歌曲的算法。在数学中,主要研究计算机能实现的算法,即按照某种机械程序步骤一定可以得到结果的解决问题的程序。(古代的计算工具:算筹与算盘. 20世纪最伟大的发明:计算机,计算机是强大的实现各种算法的工具。)
例1:解二元一次方程组: 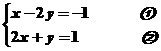
分析:解二元一次方程组的主要思想是消元的思想,有代入消元和加减消元两种消元的方法,下面用加减消元法写出它的求解过程.
解:第一步:② - ①×2,得: 5y=3; ③
第二步:解③得 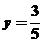 ;
第三步:将
;
第三步:将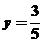 代入①,得
代入①,得 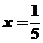 .
.
学生探究:对于一般的二元一次方程组来说,上述步骤应该怎样进一步完善? 老师评析:本题的算法是由加减消元法求解的,这个算法也适合一般的二元一次方程组的解法。下面写出求方程组的解的算法:
例2:写出求方程组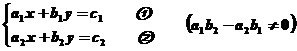 的解的算法.
的解的算法.
解:第一步:②×a1 - ①×a2,得: ③ 第二步:解③得
③ 第二步:解③得 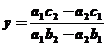 ;第三步:将
;第三步:将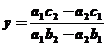 代入①,得
代入①,得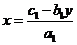
算法概念:
在数学上,现代意义上的“算法”通常是指可以用计算机来解决的某一类问题是程序或步骤,这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.
2. 算法的特点:
(1)有限性:一个算法的步骤序列是有限的,必须在有限操作之后停止,不能是无限的.
(2)确定性:算法中的每一步应该是确定的并且能有效地执行且得到确定的结果,而不应当是模棱两可.
(3)顺序性与正确性:算法从初始步骤开始,分为若干明确的步骤,每一个步骤只能有一个确定的后继步骤,前一步是后一步的前提,只有执行完前一步才能进行下一步,并且每一步都准确无误,才能完成问题.
(4)不唯一性:求解某一个问题的解法不一定是唯一的,对于一个问题可以有不同的算法.
(5)普遍性:很多具体的问题,都可以设计合理的算法去解决,如心算、计算器计算都要经过有限、事先设计好的步骤加以解决.
例题讲评:
例3、任意给定一个大于1的整数n,试设计一个程序或步骤对n是否为质数做出判断.
分析:(1)质数是只能被1和自身整除的大于1的整数.
(2)要判断一个大于1的整数n是否为质数,只要根据质数的定义,用比这个整数小的数去除n,如果它只能被1和本身整除,而不能被其它整数整除,则这个数便是质数.
解:算法:第一步:判断n是否等于2.若n=2,则n是质数;若n>2,则执行第二步.
第二步:依次从2~(n-1)检验是不是n的因数,即整除n的数.若有这样的数,则n不是质数;若没有这样的数,则n是质数.
说明:本算法是用自然语言的形式描述的.设计算法一定要做到以下要求:
(1)写出的算法必须能解决一类问题,并且能够重复使用.(2)要使算法尽量简单、步骤尽量少.
(3)要保证算法正确,且计算机能够执行.
利用TI-voyage200图形计算器演示:(学生已经被吸引住了)
例4、.用二分法设计一个求方程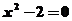 的近似根的算法.
的近似根的算法.
分析:该算法实质是求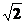 的近似值的一个最基本的方法.
的近似值的一个最基本的方法.
解:设所求近似根与精确解的差的绝对值不超过0.005,算法:
第一步:令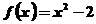 .因为
.因为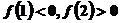 ,所以设x1=1,x2=2.
,所以设x1=1,x2=2.
第二步:令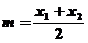 ,判断f(m)是否为0.若是,则m为所求;若否,则继续判断
,判断f(m)是否为0.若是,则m为所求;若否,则继续判断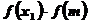 大于0还是小于0.
大于0还是小于0.
第三步:若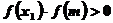 ,则x1=m;否则,令x2=m.
,则x1=m;否则,令x2=m.
第四步:判断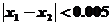 是否成立?若是,则x1、x2之间的任意值均为满足条件的近似根;若否,则返回第二步.
是否成立?若是,则x1、x2之间的任意值均为满足条件的近似根;若否,则返回第二步.
练习1:写出解方程x2-2x-3=0的一个算法。
练习2、求1×3×5×7×9×11的值,写出其算法。 练习3、有蓝和黑两个墨水瓶,但现在却错把蓝墨水装在了黑墨水瓶中,黑墨水错装在了蓝墨水瓶中,要求将其互换,请你设计算法解决这一问题。
小结
20.在竖直平面内建立xoy直角坐标系,oy表示竖直向上方向.如图所示.已知该平面内存在沿x轴正向的区域足够大的匀强电场.一带电小球从坐标原点o沿ox方向以4J的初动能竖直向上抛出.不计空气阻力,它到达的最高位置如图中M点所示.求:(1)小球在M点时的动能EkM.
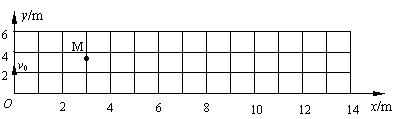 (2)设小球落回跟抛出点在同一水平面时的位置为N,求小球到达N点时的动能EkN.
(2)设小球落回跟抛出点在同一水平面时的位置为N,求小球到达N点时的动能EkN.
19. 如图,光滑绝缘半球槽的半径为R,处在水平向右的匀强电场中,一质量为m的带电小球从槽的右端A处无初速沿轨道滑下,滑到最低点B时,球对轨道的压力为2mg.求
如图,光滑绝缘半球槽的半径为R,处在水平向右的匀强电场中,一质量为m的带电小球从槽的右端A处无初速沿轨道滑下,滑到最低点B时,球对轨道的压力为2mg.求
(1)小球受到的电场力的大小和方向.
(2)带电小球在滑动过程中的最大速度.
18. 某同学用精度较高的电压表测量匀强电场中A、B、C三点的电压,得到的读数分别为UAB=4V,UCB=6V,已知AB=80cm,
某同学用精度较高的电压表测量匀强电场中A、B、C三点的电压,得到的读数分别为UAB=4V,UCB=6V,已知AB=80cm,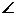 ABC=600,,BC=60cm.
ABC=600,,BC=60cm.
(1)作出该匀强电场的电场线.
(2)求场强E为多大?
17. 质量为m,带电荷量为-q的微粒(重力不计),在匀强电场中的
质量为m,带电荷量为-q的微粒(重力不计),在匀强电场中的
A点时速度为v,方向与电场线垂直,在B点 时速度大小为2V,
如图所示,已知A、B两点间的距离为d.求:
(1)A、B两点的电压;
(2)电场强度的大小和方向.
16. 如图所示,用金属丝A、B弯成半径r=1m的圆,但在AB之间留出一小缺口,
d=2cm,相对圆弧来说是很小的间隙,将电荷量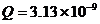 C的正电荷均匀分布
C的正电荷均匀分布
在金属丝上.求圆心O处的电场强度.
15.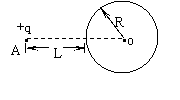 如图所示,在不带电的半径为R的导体球附近一点A处,从无限远处移来一点电荷,点电荷的电荷量为q,若A点到球面的距离为L,当达到静电平衡时,导体球上的感应电荷在球心O处产生的场强的大小等于多少?其方向如何?
如图所示,在不带电的半径为R的导体球附近一点A处,从无限远处移来一点电荷,点电荷的电荷量为q,若A点到球面的距离为L,当达到静电平衡时,导体球上的感应电荷在球心O处产生的场强的大小等于多少?其方向如何?

14.在图示的实验装置中,已充电的平行板电容器的极板A与一静电计相连接,极板B接地.若极板B稍向上移,则电容器电容 ,静电计指针偏角 ;若极板B稍向右水平移动,则电容器的带电荷量 .(填“增大”、“减小”或“不变”)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com