
20.(石景山·理·题17)
如图,已知直三棱柱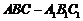 ,
,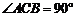 ,
, 是棱
是棱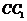 上动点,
上动点,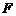 是
是 中点 ,
中点 ,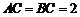 ,
,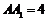 .
.
⑴求证: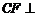 平面
平面 ;
;
⑵当 是棱
是棱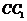 中点时,求证:
中点时,求证: ∥平面
∥平面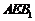 ;
;
⑶在棱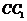 上是否存在点
上是否存在点 ,使得二面角
,使得二面角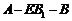 的大小是
的大小是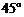 ,若存在,求
,若存在,求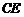 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.

[解析]
⑴证明:⑴∵三棱柱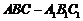 是直棱柱,∴
是直棱柱,∴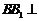 平面
平面 .
.
又∵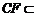 平面
平面 ,
,
∴
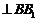 .
.
∵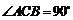 ,
,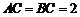 ,
,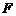 是
是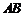 中点,
中点,
∴
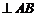 .
.
∵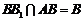 ,
,
∴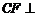 平面
平面 .
.
⑵证明:取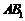 的中点
的中点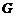 ,联结
,联结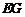 ,
,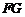 .
.

∵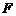 、
、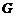 分别是棱
分别是棱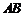 、
、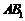 中点,
中点,
∴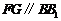 ,
,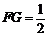
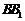 .
.
又∵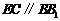 ,
,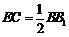 ,
,
∴ ,
,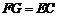 .
.
∴四边形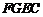 是平行四边形,
是平行四边形,
∴ ∥
∥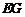 .
.
又∵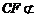 平面
平面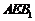 ,
,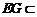 平面
平面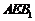 ,
,
∴ 平面
平面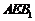 .
.
⑶以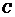 为坐标原点,射线
为坐标原点,射线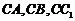 为
为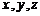 轴正半轴,建立如图所示的空间直角坐标系
轴正半轴,建立如图所示的空间直角坐标系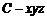 ,
,

则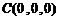 ,
,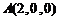 ,
,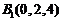 .
.
设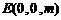 ,平面
,平面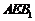 的法向量
的法向量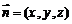 ,
,
则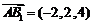 ,
, .
.
且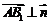 ,
,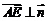 .
.
于是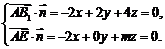
所以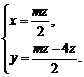
取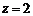 ,则
,则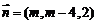
∵三棱柱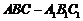 是直棱柱,
是直棱柱,
∴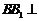 平面
平面 .
.
又∵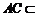 平面
平面 ,
,
∴
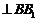 .
.
∵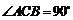 ,
,
∴
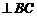 .
.
∵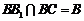 ,
,
∴
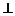 平面
平面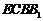 .
.
∴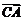 是平面
是平面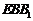 的法向量,
的法向量,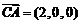 .
.
二面角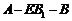 的大小是
的大小是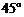 ,
,
则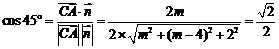 .
.
解得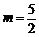 .
.
∴在棱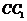 上存在点
上存在点 ,使得二面角
,使得二面角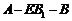 的大小是
的大小是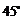 ,
,
此时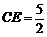 .
.
19.(丰台·文科·题16)
如图,在底面是正方形的四棱锥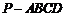 中,
中,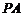
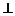 面
面 ,
,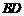 交
交 于点
于点 ,
,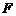 是
是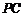 中点,
中点,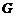 为
为 上一点.
上一点.
⑴求证: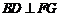 ;
;
⑵确定点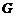 在线段
在线段 上的位置,使
上的位置,使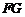 //平面
//平面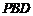 ,并说明理由.
,并说明理由.

[解析]
⑴∵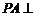 面
面 ,四边形
,四边形 是正方形,
是正方形,
其对角线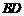 、
、 交于点
交于点 ,
,
∴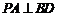 ,
,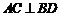 .
.
∴ 平面
平面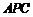 ,
,
∵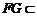 平面
平面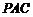 ,
,
∴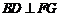

⑵当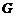 为
为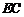 中点,即
中点,即 时,
时,
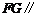 /平面
/平面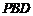 ,
,
理由如下:
连结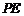 ,由
,由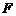 为
为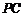 中点,
中点,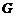 为
为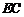 中点,知
中点,知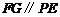 ,
,
而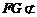 平面
平面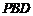 ,
,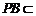 平面
平面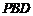 ,
,
故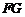 //平面
//平面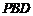 .
.
18.(丰台·理科·题16)
如图,在底面是正方形的四棱锥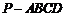 中,
中,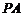
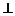 面
面 ,
,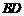 交
交 于点
于点 ,
,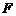 是
是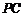 中点,
中点, 为
为 上一点.
上一点.
⑴求证: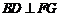 ;
;
⑵确定点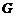 在线段
在线段 上的位置,使
上的位置,使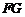 //平面
//平面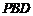 ,并说明理由.
,并说明理由.
⑶当二面角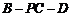 的大小为
的大小为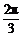 时,求
时,求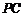 与底面
与底面 所成角的正切值.
所成角的正切值.

[解析]
⑴∵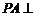 面
面 ,四边形
,四边形 是正方形,其对角线
是正方形,其对角线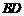 ,
, 交于点
交于点 ,
,
∴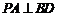 ,
,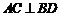 .
.
∴ 平面
平面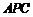 ,
,
∵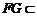 平面
平面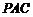 ,
,
∴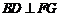
⑵当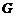 为
为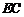 中点,即
中点,即 时,
时,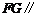 平面
平面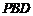 ,理由如下:
,理由如下:
连结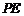 ,由
,由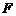 为
为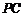 中点,
中点,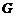 为
为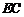 中点,知
中点,知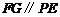 ,
,
而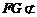 平面
平面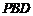 ,
,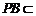 平面
平面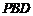 ,
,
故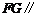 平面
平面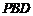 .
.
⑶作 于
于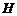 ,连结
,连结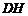 ,
,
∵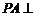 面
面 ,四边形
,四边形 是正方形,
是正方形,
∴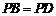 ,
,
又∵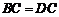 ,
,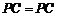 ,∴
,∴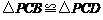 ,
,
∴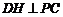 ,且
,且 ,
,
∴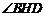 是二面角
是二面角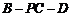 的平面角,
的平面角,
即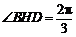 ,
,
∵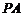 ⊥面
⊥面 ,∴
,∴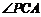 就是
就是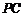 与底面
与底面 所成的角
所成的角
连结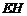 ,则
,则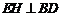 ,
,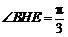 ,
,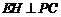
∴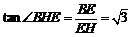 ,
,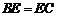
∴ ,∴
,∴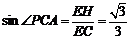 ,
,
∴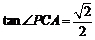
∴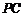 与底面
与底面 所成角的正切值是
所成角的正切值是 .
.
另解:以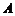 为原点,
为原点,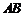 、
、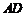 、
、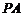 所在的直线分别为
所在的直线分别为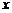 、
、 、
、 轴建立空间直角坐标系如图所示,
轴建立空间直角坐标系如图所示,
设正方形 的边长为
的边长为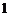 ,则
,则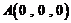 ,
,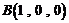 ,
,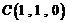 ,
,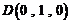 ,
,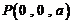
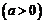 ,
,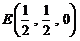 ,
,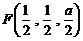 ,
,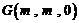
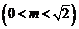 .
.
⑴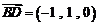 ,
, ,
,
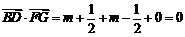
∴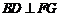

⑵要使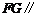 平面
平面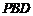 ,只需
,只需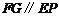 ,而
,而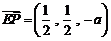 ,
,
由 可得
可得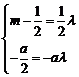 ,解得
,解得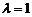 ,
,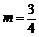 ,
,
∴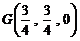 ,∴
,∴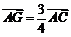
故当 时,
时,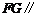 平面
平面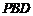
设平面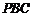 的一个法向量为
的一个法向量为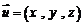 ,
,
则 ,而
,而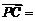
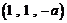 ,
,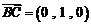 ,
,
∴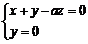 ,取
,取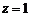 ,得
,得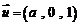 ,
,
同理可 得平面
得平面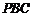 的一个法向量
的一个法向量
设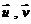 所成的角为
所成的角为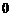 ,则
,则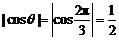 ,
,
即 ,∴
,∴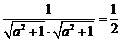 ,∴
,∴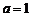
∵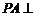 面
面 ,∴
,∴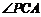 就是
就是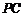 与底面
与底面 所成的角,
所成的角,
∴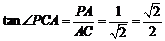 .
.
17.(海淀·文科·题17)
如图:在四棱锥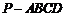 中,底面
中,底面 是菱形,
是菱形,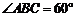 ,
,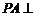 平面
平面 ,
,
点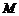 、
、 分别为
分别为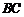 、
、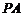 的中点,且
的中点,且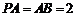 .
.

⑴证明: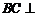 平面
平面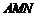 ;
;
⑵求三棱锥
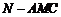 的体积;
的体积;
⑶在线段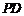 上是否存在一点
上是否存在一点 ,使得
,使得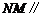 平面
平面 ;若存在,求出
;若存在,求出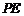 的长;若不存在,说明理由.
的长;若不存在,说明理由.
[解析]
⑴因为 为菱形,所以
为菱形,所以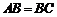
又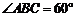 ,所以
,所以 ,
,
又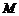 为
为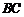 中点,所以
中点,所以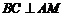
而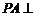 平面
平面 ,
,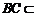 平面
平面 ,所以
,所以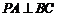
又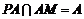 ,所以
,所以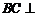 平面
平面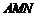
⑵因为
又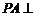 底面
底面 ,
,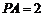 ,所以
,所以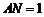
所以,三棱锥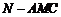 的体积
的体积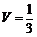

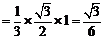
⑶存在
取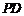 中点
中点 ,连结
,连结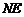 ,
,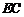 ,
,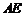 ,
,
因为 ,
, 分别为
分别为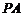 、
、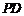 中点,所以
中点,所以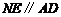 且
且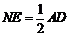
又在菱形 中,
中,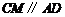 ,
,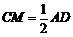
所以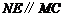 ,
,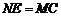 ,即
,即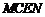 是平行四边形
是平行四边形
所以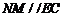 ,又
,又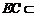 平面
平面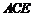 ,
, 平面
平面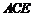
所以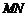
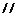 平面
平面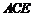 ,即在
,即在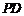 上存在一点
上存在一点 ,使得
,使得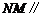 平面
平面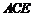 ,
,
此时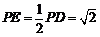 .
.
16.(海淀·理科·题17)
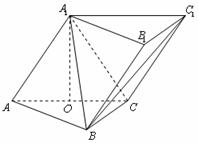
如图,三棱柱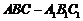 中,侧面
中,侧面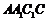
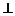 底面
底面 ,
, ,
,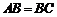 ,
,
且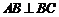 ,
, 为
为 中点.
中点.
⑴证明: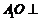 平面
平面 ;
;
⑵求直线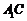 与平面
与平面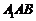 所成角的正弦值;
所成角的正弦值;
⑶在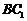 上是否存在一点
上是否存在一点 ,使得
,使得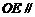 平面
平面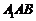 ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点 的位置.
的位置.
[解析]
⑴证明:因为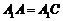 ,且
,且 为
为 的中点,所以
的中点,所以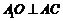 .
.
又由题意可知,平面 平面
平面 ,交线为
,交线为 ,且
,且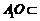 平面
平面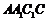 ,
,
所以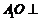 平面
平面 .
.
⑵如图,以 为原点,
为原点,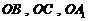 所在直线分别
所在直线分别 为
为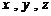 轴建立空间直角坐标系.
轴建立空间直角坐标系.
由题意可知,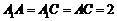 ,又
,又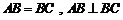
∴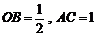 .
.
所以得: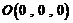 ,
,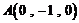 ,
,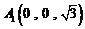 ,
,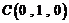 ,
,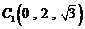 ,
,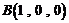 ,则有:
,则有:
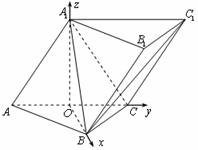
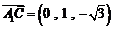 ,
,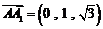 ,
, .
.
设平面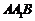 的一个法向量为
的一个法向量为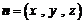 ,则有
,则有
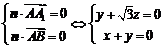 ,令
,令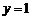 ,得
,得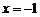 ,
,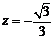
所以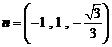 .
.
 .
.
因为直线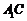 与平面
与平面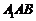 所成角
所成角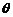 和向量
和向量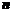 与
与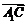 所成锐角互余,
所成锐角互余,
所以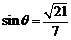 .
.
⑶设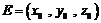 ,
,
即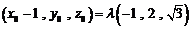 ,得
,得 .
.
所以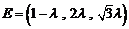 ,得
,得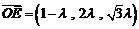
令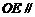 平面
平面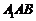 ,得
,得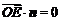 ,即
,即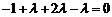 ,得
,得 ,
,
即存在这样的点 ,
, 为
为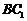 的中点.
的中点.
15.(朝阳·文·题12)
如下图所示,一个空间几何体的正视图和侧视图是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为 .

[解析]
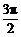 .
.
易知该几何体是底面直径为1,高为1的圆柱.
于是其全面积为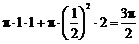 .
.
14.(朝阳·文·题8)
如图,设平面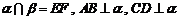 ,垂足分别为
,垂足分别为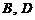 ,且
,且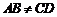 ,如果增加一个条件就能推出
,如果增加一个条件就能推出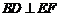 ,给出四个条件:①
,给出四个条件:①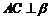 ;②
;②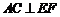 ;③
;③ 与
与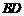 在
在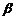 内的正投影在同一条直线上;④
内的正投影在同一条直线上;④ 与
与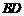 在平面
在平面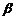 内的正投影所在直线交于一点.
那么这个条件不可能是( )
内的正投影所在直线交于一点.
那么这个条件不可能是( )
A.①② B.②③ C.③ D.④

[解析] D;
在①②③的条件下,均有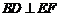 .
.
若能证明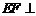 面
面 .由
.由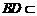 面
面 ,则可证明
,则可证明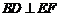 .
.
①中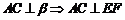 .又由
.又由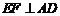 ,知
,知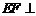 面
面 .
.
②中由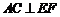 ,
,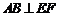 知
知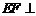 面
面 .
.
③由面 在
在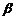 内的正投影为直线,知面
内的正投影为直线,知面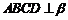 .
.
又面 ,
,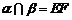 ,知
,知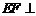 面
面 .
.
13.(朝阳·理·题8)
一个空间四边形 的四条边及对角线
的四条边及对角线 的长均为
的长均为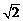 ,二面角
,二面角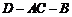 的余弦值为
的余弦值为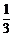 ,则下列论断正确的是 ( )
,则下列论断正确的是 ( )
A.空间四边形 的四个顶点在同一球面上且此球的表面积为
的四个顶点在同一球面上且此球的表面积为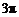 .
.
B.空间四边形 的四个顶点在同一球面上且此球的表面积为
的四个顶点在同一球面上且此球的表面积为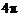
C.空间四边形 的四个顶点在同一球面上且此球的表面积为
的四个顶点在同一球面上且此球的表面积为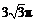
D.不存在这样的球使得空间四边形 的四个顶点在此球面上.
的四个顶点在此球面上.
[解析] A;
易知四面体 为边长为
为边长为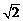 的正四面体.容易计算有其外接球的半径为
的正四面体.容易计算有其外接球的半径为 .于是外接球的表面积为
.于是外接球的表面积为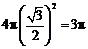 .
.
12.(朝阳·理·题4)
一个简单几何体的正视图,侧视图如图所示,则其俯视图不可能为①长方形;②正方形;③圆; ④椭圆.其中正确的是( )
A.①② B.②③
C.③④ D.①④

[解析] B;
易知其俯视图可能为边长为3,2的矩形;亦可能为半长轴为3,半短轴为2的椭圆.
11.(崇文·文·题3)
有一个几何体的三视图及其尺寸如图(单位: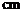 ),该几何体的表面积和体积为( )
),该几何体的表面积和体积为( )
A.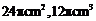 B.
B.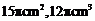 C.
C.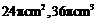 D.以上都不正确
D.以上都不正确

[解析] A;
易知几何体为母线长为5cm,底面直径为6cm的圆锥.
于是表面积为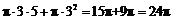 ;体积为
;体积为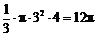 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com