
30.(朝阳·理·题17)
如图,在三棱柱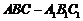 中,每个侧面均为正方形,
中,每个侧面均为正方形,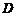 为底边
为底边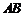 的中点,
的中点, 为侧棱
为侧棱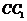 的中点.
的中点.
⑴求证: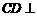 平面
平面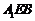 ;
;
⑵求证: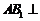 平面
平面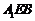 ;
;
⑶求直线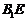 与平面
与平面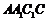 所成角的正弦值.
所成角的正弦值.

[解析]
⑴设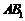 和
和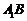 的交点为
的交点为 ,连接
,连接 ,连接
,连接 ,
,
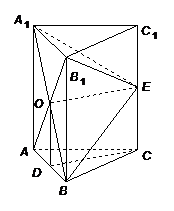
因为 为
为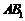 的中点,
的中点,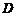 为
为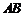 的中点,
的中点,
所以 ,且
,且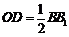 又
又 是
是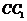 中点,
中点,
则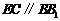 且
且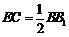 ,
,
所以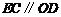 且
且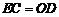 .
.
所以四边形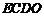 为平行四边形,
为平行四边形,
所以 .
.
又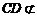 平面
平面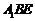 ,
,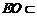 平面
平面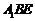 ,
,
则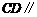 平面
平面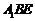 ……………………5分
……………………5分
⑵因为三棱柱各侧面都是正方形,
所以 ,
,
所以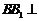 平面
平面 .
.
因为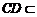 平面
平面 ,所以
,所以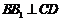 .
.
由已知得 ,
,
所以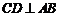 .
.
所以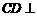 平面
平面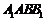
由⑴可知 ,
,
所以 平面
平面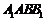 .
.
所以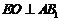 .
.
因为侧面是正方形,所以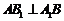 .
.
又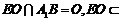 平面
平面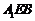 ,
,
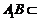 平面
平面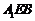 .
.
所以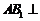 平面
平面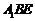 .
.
⑶取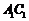 中点
中点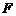 ,连接
,连接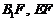 .
.

在三棱柱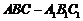 中,
中,
因为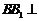 平面
平面
所以侧面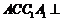 底面
底面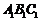 .
.
因为底面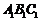 是正三角形,且
是正三角形,且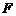 是
是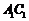 中点,
中点,
所以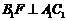 ,所以
,所以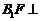 侧面
侧面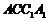 .
.
所以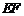 是
是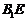 在平面
在平面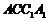 上的射影,
上的射影,
所以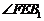 是
是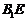 与平面
与平面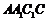 所成角.
所成角.
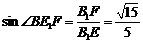 . ………………14分
. ………………14分
解法二:如图所示,建立空 间直角坐标系.
间直角坐标系.

设边长为2,可求得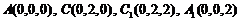 ,
,
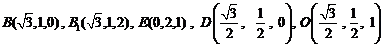 .
.
⑴易知,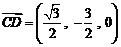 ,
,
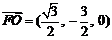 ,所以
,所以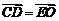 ,所以
,所以 .
.
又 ,则
,则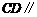 平面
平面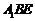 …………5分
…………5分
⑵易得,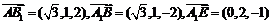
所以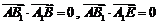 .
.
所以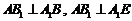 .
.
又因为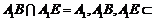 平面
平面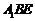 .
.
所以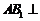 平面
平面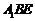 .………………10分
.………………10分
⑶设侧面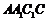 的法向量为
的法向量为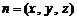 .
.
因为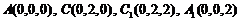 .
.
所以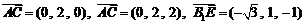 .
.
由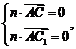 得
得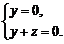 解得
解得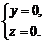 .
.
不妨令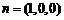 ,设直线
,设直线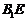 与平面
与平面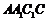 所成角为
所成角为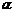 ,
,
所以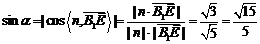 .
.
所以直线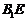 与平面
与平面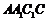 所成角的正弦值为
所成角的正弦值为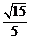 .
.
29.(崇文·文·题17)
三棱柱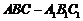 中,侧棱与底面垂直,
中,侧棱与底面垂直,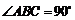 ,
,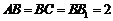 ,
, 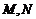 分别是
分别是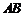 ,
,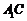 的中点.
的中点.
⑴求证: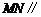 平面
平面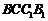 ;
;
⑵求证: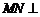 平面
平面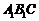 ;
;
⑶求三棱锥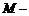
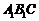 的体积.
的体积.

[解析]
⑴连结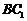 ,
,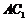 ,
,
∵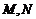 是
是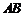 ,
,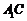 的中点
的中点
∴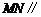
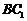 .
.
又∵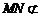 平面
平面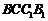 ,
,
∴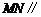 平面
平面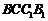 .
.
⑵∵三棱柱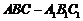 中,侧棱与底面垂直,
中,侧棱与底面垂直,
∴四边形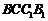 是正方形.
是正方形.
∴ .
.
∴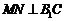 .
.
连结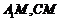 ,
,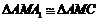 .
.
∴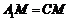 ,
, 又
又 中
中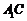 的中点,
的中点,
∴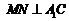 .
.
∵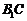 与
与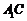 相交于点
相交于点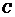 ,
,
∴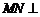 平面
平面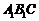 .
.
⑶由⑵知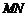 是三棱锥
是三棱锥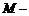
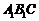 的高.
的高.
在直角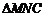 中,
中,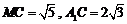 ,
,
∴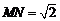 .
.
又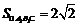 .
.
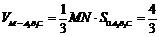 .
.
28.(崇文·理·题17)
三棱柱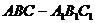 中,侧棱与底面垂直,
中,侧棱与底面垂直,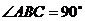 ,
,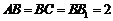 ,
, 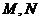 分别是
分别是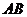 ,
,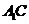 的中点.
的中点.
⑴求证: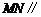 平面
平面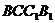 ;
;
⑵求证: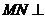 平面
平面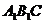 ;
;
⑶求二面角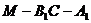 的余弦值.
的余弦值.

[解析]
⑴连结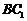 ,
,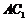 .在
.在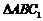 中,
中,
∵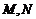 是
是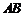 ,
,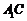 的中点,∴
的中点,∴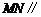
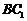 .
.
又∵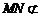 平面
平面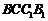 ,
,
∴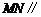 平面
平面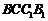 .
--------------------4分
.
--------------------4分
⑵如图,以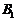 为原点建立空间直角坐标系
为原点建立空间直角坐标系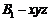 .
.
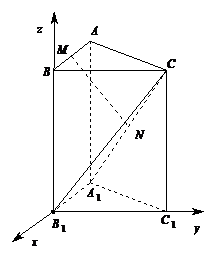
则 ,
,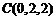 ,
,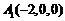 ,
,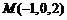 ,
,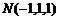
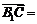
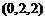 ,
,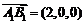 ,
,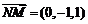 .
.
设平面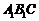 的法向量为
的法向量为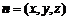 .
.
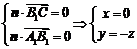
令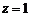 ,则
,则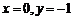 ,∴
,∴ 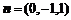 .∴
.∴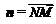 .
.
∴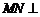 平面
平面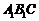 .
--------------------9分
.
--------------------9分
⑶设平面 的法向量为
的法向量为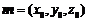 ,
,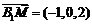 .
.
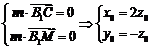
令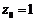 ,则
,则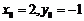
∴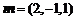 .
.
∴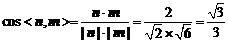 .
.
所求二面角 的余弦值为
的余弦值为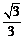 .
.
27.(宣武·文·题16)
如图,在四棱锥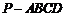 中,
中,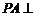 平面
平面 ,底面
,底面 为直角梯形,
为直角梯形,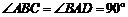 ,
,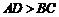 ,
,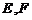 分别为棱
分别为棱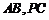 的中点.
的中点.
⑴求证: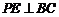 ;
;
⑵求证: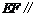 平面
平面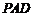 .
.

[解析]
⑴∵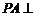 平面
平面 ,
,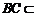 平面
平面
∴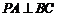
∵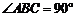
∴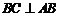
∴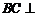 平面
平面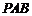
又 是
是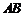 中点,
中点,
∴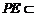 平面
平面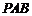
∴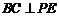 .
.
⑵证明:取 中点
中点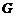 ,连结
,连结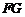 ,
,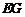 ,
,

∵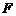 为
为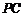 中点,∴
中点,∴ .
.
∵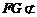 平面
平面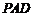 ,
,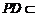 平面
平面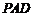 , [
, [
∴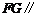 平面
平面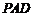 ;
;
同理,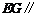 平面
平面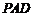 .
.
∵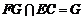 ,
,
∴平面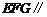 平面
平面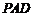 .
.
∴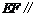 平面
平面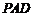 .
.
26.(宣武·理·题16)
如图,在四棱锥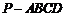 中,
中,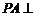 平面
平面 ,底面
,底面 为直角梯形,
为直角梯形,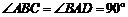 ,
,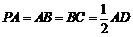 .
. 为
为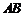 中点,
中点,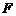 为
为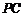 中点.
中点.
⑴求证: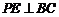 ;
;
⑵求二面角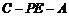 的余弦值;
的余弦值;
⑶若四棱锥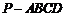 的体积为
的体积为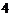 ,求
,求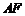 的长.
的长.

[解析]
⑴∵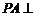 平面
平面 ,
,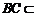 平面
平面
∴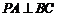
∵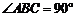
∴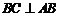
∴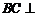 平面
平面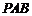
又 是
是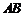 中点,
中点,
∴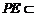 平面
平面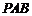
∴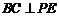 .
.
⑵建立直角坐标系 ,设
,设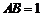
则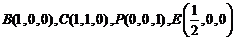
∴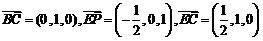
由⑴知,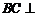 平面
平面 ,
,
∴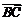 是平面
是平面 的法向量.
的法向量.
设平面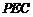 的法向量为
的法向量为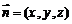 ,
,
则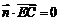 且
且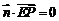 ,
,
∴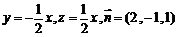 .
.
∴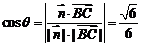 ,
,
二面角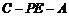 的余弦值为
的余弦值为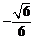 .
.
⑶连结 ,设
,设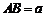 ,
,
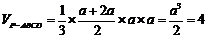 ,∴
,∴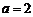 .
.
∵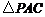 是直角三角形,
是直角三角形,
∴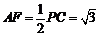 .
.
25.(东城·文·题17)
三棱柱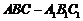 中,
中,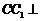 平面
平面 ,
,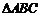 是边长为
是边长为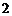 的等边三角形,
的等边三角形,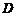 为
为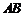 边中点,且
边中点,且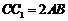 .
.
⑴求证:平面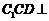 平面
平面 ;
;
⑵求证: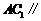 平面
平面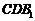 ;
;
⑶求三棱锥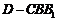 的体积.
的体积.

[解析]
⑴因为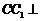 平面
平面 ,又
,又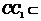 平面
平面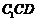 ,
,
所以平面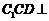 平面
平面 .
.
⑵证明:连结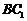 交
交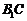 于
于 ,连结
,连结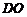 ,则
,则 是
是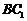 的中点,
的中点,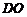 是
是 的中位线.
的中位线.
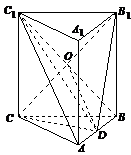
所以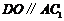 .
.
因为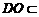 平面
平面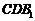 ,所以
,所以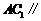 平面
平面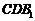 ;
;
⑶因为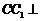 平面
平面 ,所以
,所以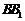
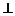 平面
平面 ,所以
,所以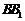 为三棱锥
为三棱锥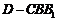 的高.
的高.
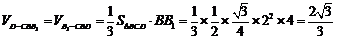 .
.
所以三棱锥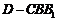 的体积为
的体积为 .
.
24.(东城·理·题17)
如图所示,在边长为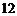 的正方形
的正方形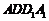 中,点
中,点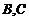 在线段
在线段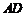 上,且
上,且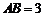 ,
,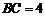 ,作
,作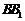
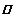
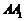 ,分别交
,分别交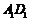 ,
,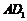 于点
于点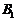 ,
,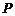 ,作
,作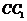
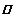
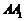 ,分别交
,分别交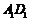 ,
,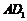 于点
于点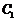 ,
,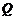 ,将该正方形沿
,将该正方形沿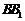 ,
,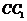 折叠,使得
折叠,使得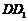 与
与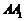 重合,构成如图所示的三棱柱
重合,构成如图所示的三棱柱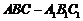 .
.
⑴求证: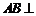 平面
平面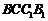 ;
;
⑵求四棱锥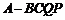 的体积;
的体积;
⑶求平面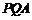 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.

[解析]
⑴在正方形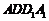 中,因为
中,因为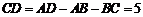 ,
,
所以三棱柱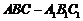 的底面三角形
的底面三角形 的边
的边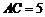 .
.
因为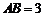 ,
,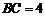 ,
,
所以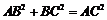 ,所以
,所以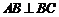 .
.
因为四边形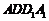 为正方形,
为正方形,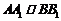 ,
,
所以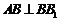 ,而
,而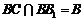 ,
,
所以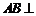 平面
平面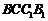 .
.
⑵因为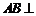 平面
平面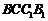 ,所以
,所以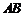 为四棱锥
为四棱锥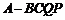 的高.
的高.
因为四边形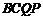 为直角梯形,且
为直角梯形,且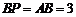 ,
, ,
,
所以梯形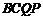 的面积为
的面积为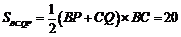 .
.
所以四棱锥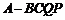 的体积
的体积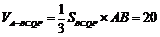 .
.
⑶由⑴、⑵可知,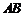 ,
,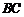 ,
,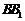 两两互相垂直.以
两两互相垂直.以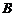 为原点,建立如图所示的空间直角坐标系
为原点,建立如图所示的空间直角坐标系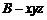 ,
,

则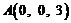 ,
,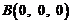 ,
,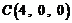 ,
,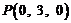 ,
,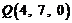 ,
,
所以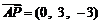 ,
,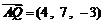 ,
,
设平面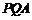 的一个法向量为
的一个法向量为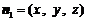 .
.
则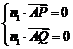 ,即
,即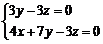 .
.
令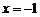 ,则
,则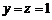 .所以
.所以 .
.
显然平面 的一个法向量为
的一个法向量为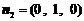 .
.
设平面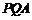 与平面
与平面 所成锐二面角为
所成锐二面角为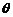 ,
,
则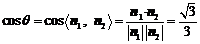 .
.
所以平面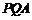 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为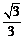 .
.
23.(西城·文·题17)
如图,在三棱锥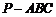 中,
中,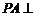 平面
平面 ,
,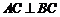 ,
,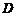 为侧棱
为侧棱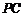 上一点,
上一点,
它的正(主)视图和侧(左)视图如图所示.
⑴证明: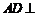 平面
平面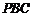 ;
;
⑵求三棱锥 的体积;
的体积;
⑶在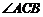 的平分线上确定一点
的平分线上确定一点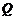 ,使得
,使得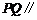 平面
平面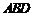 ,并求此时
,并求此时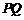 的长.
的长.
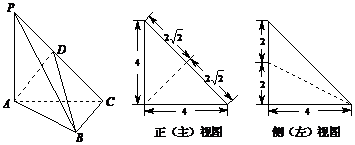
[解析]
⑴因为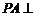 平面
平面 ,所以
,所以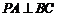 ,
,
又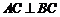 ,所以
,所以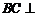 平面
平面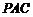 ,所以
,所以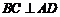 .
.
由三视图可得,在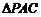 中,
中,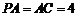 ,
,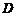 为
为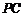 中点,所以
中点,所以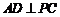 ,
,
所以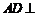 平面
平面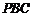 ,
,
⑵由三视图可得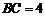 ,
,
由⑴知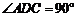 ,
,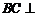 平面
平面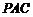 ,
,
又三棱锥 的体积即为三棱锥
的体积即为三棱锥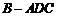 的体积,
的体积,
所以,所求三棱锥的体积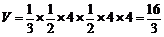 .
.
⑶取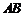 的中点
的中点 ,连接
,连接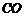 并延长至
并延长至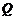 ,使得
,使得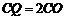 ,点
,点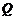 即为所求.
即为所求.

因为 为
为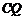 中点,所以
中点,所以 ,
,
因为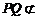 平面
平面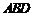 ,
,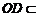 平面
平面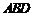 ,所以
,所以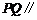 平面
平面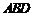 ,
,
连接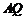 ,
,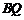 ,四边形
,四边形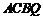 的对角线互相平分,
的对角线互相平分,
所以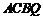 为平行四边形,所以
为平行四边形,所以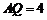 ,又
,又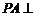 平面
平面 ,
,
所以在直角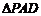 中,
中,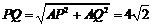 .
.
22.(西城·理·题17)
在四棱锥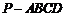 中,侧面
中,侧面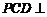 底面
底面 ,
,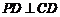 ,
, 为
为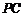 中点,底面
中点,底面 是直角梯形,
是直角梯形,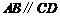 ,
,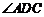 =90°,
=90°,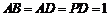 ,
,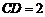 .
.
⑴求证: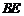
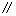 平面
平面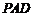 ;
;
⑵求证: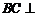 平面
平面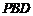 ;
;
⑶设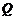 为侧棱
为侧棱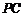 上一点,
上一点,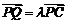 ,试确定
,试确定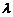 的值,使得二面角
的值,使得二面角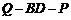 为45°.
为45°.
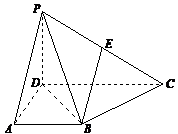
[解析]
⑴取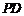 的中点
的中点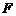 ,连结
,连结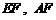 ,
,
因为 为
为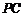 中点,所以
中点,所以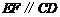 ,且
,且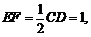
在梯形 中,
中,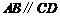 ,
,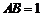 ,
,
所以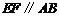 ,
,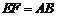 ,四边形
,四边形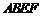 为平行四边形,
为平行四边形,
所以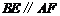 ,
,
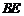
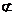 平面
平面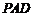 ,
,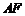
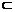 平面
平面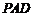 ,
,
所以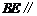 平面
平面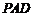 .
.
⑵平面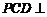 底面
底面 ,
,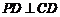 ,所以
,所以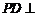 平面
平面 ,所以
,所以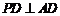 .
.
如图,以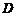 为原点建立空间直角坐标系
为原点建立空间直角坐标系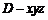 .
.
则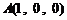 ,
,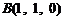 ,
,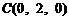 ,
,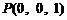 .
.
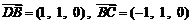 .
.
所以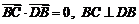 .
.
又由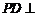 平面
平面 ,可得
,可得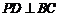 ,
,
所以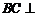 平面
平面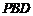 .
.

⑶平面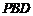 的法向量为
的法向量为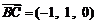 ,
,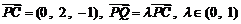 ,
,
所以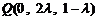 ,
,
设平面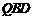 的法向量为
的法向量为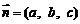 ,
,
由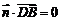 ,
,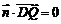 ,得
,得 ,
,
所以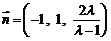 ,
,
所以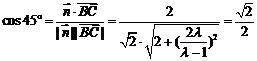 ,
,
注意到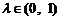 ,得
,得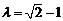 .
.
21.(石景山·文·题17)
如图,已知直三棱柱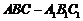 ,
,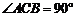 ,
,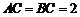 ,
,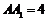 .
. 、
、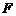 分别是棱
分别是棱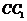 、
、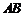 中点.
中点.
⑴求证: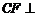
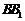 ;
;
⑵求四棱锥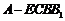 的体积;
的体积;
⑶判断直线 和平面
和平面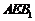 的位置关系,并加以证明.
的位置关系,并加以证明.

[解析]
⑴∵三棱柱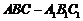 是直棱柱,
是直棱柱,
∴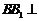 平面
平面 .
.
又∵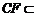 平面
平面 ,
,
∴
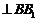 .
.
⑵解:∵三棱柱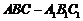 是直棱柱,
是直棱柱,
∴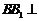 平面
平面 .
.
又∵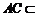 平面
平面 ,
,
∴
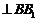 .
.
∵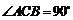 ,
,
∴
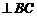 .
.
∵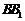
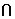
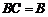 ,
,
∴
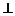 平面
平面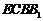 .
.
∴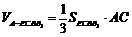 .
.
∵ 是棱
是棱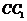 的中点,
的中点,
∴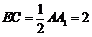 .
.
∴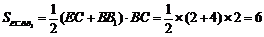 .
.
∴ .
.
⑶解: 平面
平面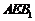 .证明如下:
.证明如下:
取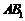 的中点
的中点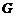 ,联结
,联结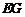 ,
,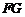 .
.

∵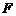 、
、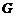 分别是棱
分别是棱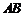 、
、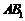 中点,
中点,
∴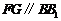 ,
,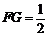
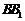 .
.
又∵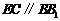 ,
,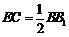 ,
,
∴ ,
,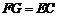 .
.
∴四边形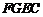 是平行四边形,
是平行四边形,
∴ ∥
∥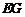 .
.
又∵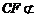 平面
平面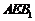 ,
,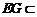 平面
平面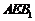 ,
,
∴ 平面
平面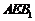 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com