1．甲物体追赶前方的乙物体，若甲的速度大于乙的速度，则两者之间的距离　　　 。若甲的速度小于乙的速度，则两者之间的距离　　　　 。若一段时间内两者速度相等，则两者之间的距离　　　　 。

2．正确理解图象的意义

(1)首先明确所给的图象是什么图象。即认清图象中横纵轴所代表的物理量及它们的函数关系。特别是那些图形相似容易混淆的图象，更要注意区分。

(2)要清楚地理解图象中的“点”、“线”、“斜率”、“截距”、“面积”的物理意义。

①点：图线上的每一个点对应研究对象的一个状态，特别注意“起点”、“终点”、“拐点”，它们往往对应一个特殊状态。

②线：表示研究对象的变化过程和规律，如v－t图象中图线若为倾斜直线，则表示物体做匀变速直线运动。

③斜率：表示横、纵坐标上两物理量的比值，常有一个重要的物理量与之对应。用于求解定量计算对应物理量的大小和定性分析变化的快慢问题。如s－t图象的斜率表示速度大小，v－t图象的斜率表示加速度大小。

④面积；图线与坐标轴围成的面积常与某一表示过程的物理量相对应。如v－t图象与横轴包围的“面积”大小表示位移大小。

⑤截距：表示横、纵坐标两物理量在“边界”条件下的物理量的大小。由此往往能得到一个很有意义的物理量。

[典题例析]

类型一：S - t 图象的应用

例1．甲、乙、丙三物体同时同地开始做直线运动，其s-t图象如图所示，则在t₀时间内，甲、乙、丙位移大小关系是　　　　　　 ，(填“＞”、“＝”或“＜") ，路程关系是　　　　　　 ，平均速度的大小关系分别是：v_甲____v_乙____v_丙，

平均速率关系为v ’_甲____v ’_乙____v ’_丙．

类型二：v - t 图象的应用

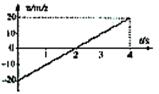例2．如图所示为一物体做匀变速直线运动的速度图线，根据图线作出的以下几个判断中，正确的是()

A．物体始终沿正方向运动　

B．物体先沿负方向运动，在t＝2s后开始沿正方向运动　

C．在t＝2s前物体位于出发点负方向上，在t＝2s后位于出发点正方向上　

D．在t＝2s时，物体距出发点最远

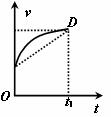
例3．如图所示为一物体运动的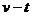图象，物体的初速度为v₀，末速度为v_t，在时间t₁内的平均速度为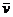，则由图可知　 (　 )

A．该物体做曲线运动　　　　　 B．该物体做非匀变速直线运动

C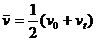．　　　　　　 D．

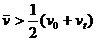
类型三：利用v - t 图象巧解问题

例4．甲、乙两物体从同一位置同时开始朝同向做直线运动，甲做初速度为零加速度为a的匀加速直线运动，经时间t₁速度达到v，发生的位移为s；乙物体先做初速度为零加速度为a₁(a₁>a)的匀加速直线运动，接着又做加速度为a₂(a₂< a)的匀加速直线运动，待发生位移s时，速度也为v，所用的总时间为t₂，则t₁和t₂的关系　 ( 　)

A．t₁> t₂　　　　 B．t₁< t₂　　　 C．t₁= t₂　　　　 D．无法确定

　 类型四：a - t 图象的应用

例5．一物体在A、B两点的正中间由静止开始运动(设不会超越A、B)，其加速度随时间变化如图所示．设向A的加速度为为正方向，若从出发开始计时，则物体的运动情况是(　 )

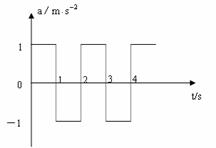A．先向A ，后向B，再向A，又向B，4秒末静止在原处

B．先向A ，后向B，再向A，又向B，4秒末静止在偏向A

的某点

C．先向A ，后向B，再向A，又向B，4秒末静止在偏向B

的某点

D．一直向A运动，4秒末静止在偏向A的某点

[问题反思]

第5课时　运动中的追及和相遇问题

[知识回顾]

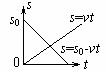
1． s-t、v-t、a-t图像的比较。

	位移图象(s-t)	速度图象(v-t)	加速度图象(a-t)
匀速直线运动
匀加速直线运动 (a>0，s有最小值)	抛物线(不要求)
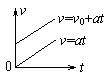匀减速直线运动 (a<0，s有最大值)	抛物线(不要求)
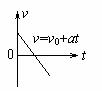备注	位移图线的斜率表示速度	①斜率表示加速度 ②图线与横轴所围面积表示位移，横轴上方“面积”为正，下方为负

4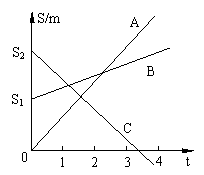．如右图为s-t图象， A描述的是　　　　　　　　　 运动；B描述的是　　　　　　　　　　　　　　　　　 运动；C描述的是　　　　　　　　　　　　　　 运动。

图中A、B的斜率为　　　　　 (“正”或“负”)，表示物体向　　　　　　 运动；C的斜率为　　 (“正”或“负”)，表示C向　　　　　 运动。A的速度　　　 (“大于”、“等于”或“小于”)B的速度。

[考点突破]

3．如右图为图象， A描述的是　　　　　　　　　 运动；B描述的是　　　　　　　　　　　　　　　　　 运动；C描述的是　　　　　　　　　　　　　　 运动。

图中A、B的斜率为　　　　 (“正”或“负”)，表示物体作　　　　　　 运动；C的斜率为　　 (“正”或“负”)，表示C作　　　　　 运动。A的加速度　　　 (“大于”、“等于”或“小于”)B的加速度。图线与横轴t所围的面积表示物体运动的　　　　　　　 。

2．匀变速直线运动的图象是　　　　　　　　　　　　　

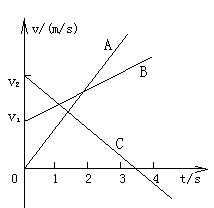从图象上可以看出某一时刻瞬时速度的大小。可以根据图象求一段时间内的位移，其位移为　　　　　　　 还可以根据图象求加速度，其加速度的大小等于　　　　 　　　　即a＝　　　　 ，　　　　 ____________越大，加速度也越大，反之则越小

、区分s-t图象、图象

[典题例析]

类型一：自由落体

例1．一个物体从H高处自由下落，经过最后196m所用的时间是4s，求H及物体下落H所用的总时间T。(空气阻力不计，g取9.8m/s²)

例2．一只小球自屋檐自由下落，在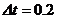s内通过高为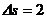m的窗口，问窗口的顶端距屋檐多高？(g=10m/s²)　

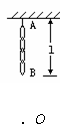
例3．一条铁链AB长为0.49m，悬于A端使其自然下垂，然后让它自由下落，求整个铁链通过悬点下方2.45m处的小孔O时需要的时间是多少？

例4．房檐滴水，每隔相等时间积成一滴水下落，当第1滴水落地时，第5滴刚好形成，观察到第4滴、第5滴距离约1m，则房檐高为(g取10m/s²)　 (　 )

A．4m　　　　　 B．5m　　　　 C．6m　　　　　 D．16m

例5．某人在室内以窗户为背景摄影时，恰好把窗外从高处落下的一个小石子摄在照片中，已知本次摄影的曝光时间是0.02s，量得照片中石子运动痕迹的长度为1.6cm，实际长度为100cm的窗框在照片中的长度为4.0cm．凭以上数据，你知道这个石子闯入镜头时大约已经运动了多长时间？(g=10m/s²)　 (　 )

类型二：竖直上抛

例6． A、B两棒长均为L＝1m，A的下端和B的上端相距S＝20m．若A、B同时运动，A做自由落体，B做竖直上抛，初速度V₀＝40m/s，求：(1)A、B两棒何时相遇？(2)从相遇开始到分离所需的时间？

例7． 一跳水运动员从离水面10m高的平台上跃起，举双臂直立身体离开台面，此时中心位于从手到脚全长的中点，跃起后重心升高0.45m达到最高点，落水时身体竖直，手先入水(在此过程中运动员水平方向的运动忽略不计)从离开跳台到手触水面，他可用于完成空中动作的时间是多少？(g取10m/s²结果保留两位数字)　

类型三：空中相遇问题、巧取参考系简化解题

例8．从12m高的平台边缘有一小球A自由落下，此时恰有一小球B在A球正下方从地面上以20m/s的初速度竖直上抛．求：(1)经过多长时间两球在空中相遇； (2)相遇时两球的速度v_A、v_B； (3)若要使两球能在空中相遇，B球上抛的初速度最小必须为多少？(取g=10m/s²)　

[问题反思]

第4课时　运动图像的探究分析及应用

[知识回顾]

1．匀速直线运动的x-t图象是一条　　　　　　　　　 。速度的大小在数值上等于　　　　　　 ，即v＝　　　　 。

(1)只在重力作用下的直线运动．

(2)v₀≠0，a＝－g．

(3)上升到最高点的时间t＝v₀/g．

(4)上升的最大高度H＝v₀²/2g．

(5)时间对称性：t_上＝t_下，即上升阶段与下降阶段抛体通过同一段竖直距离所用的时间相等．

(6)速度对称性；V_上＝－V_下，即上升阶段与下降阶段经过同一位置时的速度大小相等，方向相反．

21．把下面的句子改写成排比句。(3分)

　　 音乐家常把灵感变为跳跃的音符，文学家呢，他们优美的辞章往往缘于灵感，至于画家，他们完满的构图也常常与灵感相关，而一般人的灵感，则常是霎时的喜悦。

　　 答：　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　 22．根据下面的提示，仿写句子。(3分)

山对海说：你博大辽远，深邃宽容，是值得我尊敬的老师。

海对山说：　　　　　　　　　　　　　　　　　　　　　　　 。