
3、函数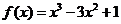 的极小值为
的极小值为
A、2
B、1 C、 D、
D、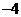
2、设全集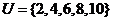 ,集合
,集合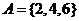 ,
,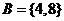 ,则
,则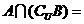
A、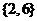 B、
B、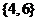 C、
C、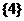 D、
D、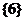
1、若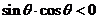 ,则
,则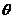 在
在
A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限
8. (海淀·理科·题12)
在二项式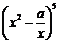 的展开式中,
的展开式中,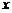 的系数是
的系数是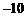 ,则实数
,则实数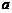 的值为
.
的值为
.
[解析] 1;
由二项式定理,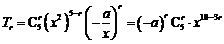 .
.
当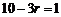 时,
时,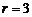 ,于是
,于是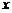 的系数为
的系数为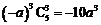 ,从而
,从而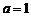 .
.
7. (崇文·理·题10)
若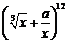 的展开式中的常数项为
的展开式中的常数项为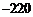 ,则实数
,则实数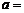
 ___________.
___________.
[解析]
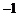 ;
;
由二项式定理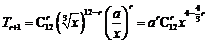 .令
.令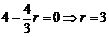 .
.
于是有 .
.
6. (石景山·理·题9)
二项式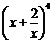 的展开式中的常数项为_____________,展开式中各项系数和为 .(用数字作答)
的展开式中的常数项为_____________,展开式中各项系数和为 .(用数字作答)
[解析]
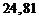 ;
;
通项公式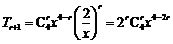 ,
,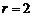 时,可得常数项
时,可得常数项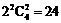 ;令
;令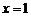 即可得各项系数和为
即可得各项系数和为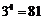 .
.
5. (崇文·理·题7)
2位男生和3位女生共5位同学站成一排.若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数为 ( )
A.36 B.42 C. 48 D.60
[解析] C;
不妨将5个位置从左到右编号为1,2,3,4,5.于是甲只能位于2,3,4号位.
i) 当甲位于2号位时,3位女生必须分别位于1,3,4位或者1,4,5位.于是相应的排法总数为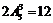 ;
;
ii) 当甲位于3号位时,3位女生必须分别位于1,2,4位或者1,2,5位或者1,4,5或者2,4,5位.于是相应的排法总数为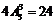 .
.
iii) 当甲位于4号位时,情形与i)相同.排法总数为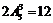 .
.
综上,知本题所有的排法数为12+24+12=48.
4. (西城·理·题6)
某会议室第一排共有8个座位,现有3人就座,若要求每人左右均有空位,那么不同的坐法种数为( )
A.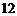 B.16 C.24 D.32
B.16 C.24 D.32
[解析] C;
将三个人插入五个空位中间的四个空档中,有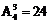 种排法.
种排法.
3. (丰台·理科·题5)
从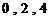 中取一个数字,从
中取一个数字,从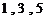 中取两个数字,组成无重复数字的三位数,则所有不同的三位数的个数是( )
中取两个数字,组成无重复数字的三位数,则所有不同的三位数的个数是( )
A.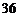 B.
B.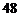 C.
C.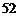 D.
D.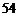
[解析] B;
从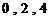 中取一个数字,从
中取一个数字,从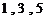 中取两个数字进行排列,然后在得到的排列中去掉首数字为
中取两个数字进行排列,然后在得到的排列中去掉首数字为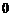 的即满足题意,因此
的即满足题意,因此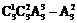
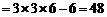 为所求.
为所求.
2. (东城·理·题4)
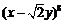 的展开式中
的展开式中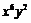 项的系数是( )
项的系数是( )
A. B.
B.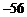 C.
C.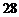 D.
D.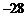
[解析] A;
所求系数为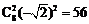 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com