
20.(本小题满分14分)解:(以下仅供参考,不同结论请酌情给分。每个正确结论给2分,证明给5分) 可以得出有以下结论:
(Ⅰ)三个侧面OAB、OAC、OBC两两互相垂直(或OA⊥BC、OB⊥AC、OC⊥AB)
(Ⅱ)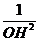 =
=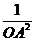 +
+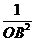 +
+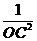 (H为ΔABC的重心)
(H为ΔABC的重心)
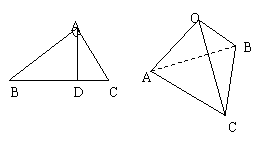 (Ⅲ)
(Ⅲ)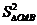 +
+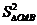 +
+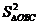 =
=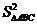
以下给出具体的证明:
(1)证明:∵OA⊥OC,OB⊥OC ∴OC⊥平面OAB
∴平面OAC⊥平面OAB 平面OBC⊥平面OAB 同理可证平面OBC⊥平面OAC
(2)证明:如图二 连接AH并延长AH交BC于D连接OD
∵OA⊥面OBC∴OA⊥OD
在RtΔABC中 ∵OH⊥OD ∴OH·AD=AO·OD
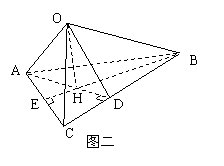 ∴OH2·AD2=AO2·OD2
∴OH2·AD2=AO2·OD2
又∵AD2=
OA2+ OD2
∴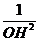 =
=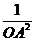 +
+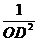
∵AD⊥BC,由三垂线定理得:BC⊥OD
∴在RtΔOBC中 OD2 ·BC2 =BO2·CO2
∴OD2=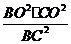 又∵BC2= BO2+CO2
又∵BC2= BO2+CO2
∴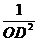 =
=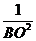 +
+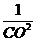 ② 由①②得:
② 由①②得: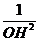 =
=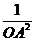 +
+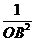 +
+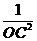
(Ⅳ) 证明:如图二(延用(Ⅸ)中的字母a,b,c)∵H为垂心 ∴AD⊥BC
又∵OA、OB、OC两两垂直 ∴SΔOAB=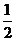 ab SΔOBC=
ab SΔOBC=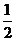 bc SΔOAC=
bc SΔOAC=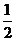 ac K^S*
ac K^S*
SΔABC=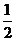 BC·AD
BC·AD
∴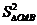 +
+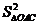 +
+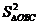 =
=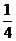 ( a2 b2+ b2 c2+ a2
c2)=
( a2 b2+ b2 c2+ a2
c2)= 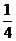 a2(b2+ c2)+
a2(b2+ c2)+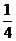 b2 c2…………①
b2 c2…………①
又∵在RtΔBOC中,OD⊥BC ∴OB2·OC2= b2 c2=OD2·BC2=OD2·(b2+ c2)………②
∴②代入①得: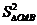 +
+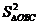 +
+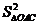 =
=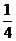 (b2+ c2)·AD2=
(b2+ c2)·AD2=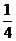 BC2·AD2=
BC2·AD2=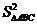
19. (本小题满分13分)解:
(1)当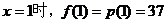 ,………1分
,………1分
当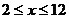 ,且
,且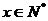 时,
时,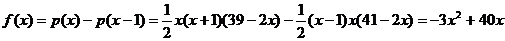 .
.
………5分
验证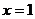 符合
符合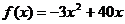 (x∈N*,且
(x∈N*,且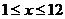 ).………6分
).………6分
(2)该商场预计第x月销售该商品的月利润为:
g(x)=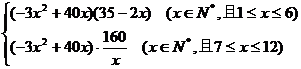
=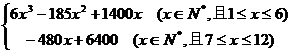 ………8分
………8分
当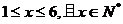 时
时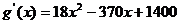 ,
,
令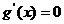 ,解得
,解得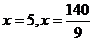 (舍去).
(舍去).
当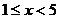 时,g′(x) >0,当
时,g′(x) >0,当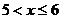 时,g′(x) <0,
时,g′(x) <0,
∴当x=5时,g(x)max=g(5)=3125(元). ………10分
当 时,
时,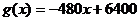 是减函数,
是减函数,
当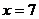 时,
时,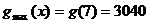 (元), ………12分
(元), ………12分
综上,商场2009年第5月份的月利润最大,最大利润为3125元. ………13分
18. (本小题满分13分)解:(1)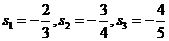 ………3分
………3分
(2)猜想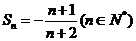 ,………5分 证明如下:
,………5分 证明如下:
①当n=1时,由(1)知结论成立;………6分
②设n=k时结论成立,即 ,则当n=k+1时,有
,则当n=k+1时,有
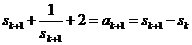 ,即
,即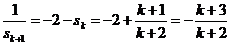
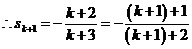 ,∴n=k+1时结论成立………12分
,∴n=k+1时结论成立………12分
综合①②知道:对任意的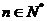 ,都有
,都有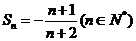 成立………13分
成立………13分
令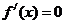 得
得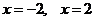 列表……………………8分
列表……………………8分
由上表知:f(x)在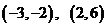 上递增;在
上递增;在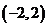 上递减…………9分
上递减…………9分
(2)由(1)知:f(x)的极大值是: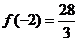 ,f(x)的极小值是:
,f(x)的极小值是: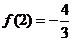
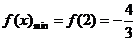 ,f(x)无最大值…………13分
,f(x)无最大值…………13分
17. (本小题满分13分) 解:联立方程解得交点坐标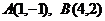 ………4分
………4分
面积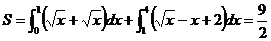 ………13分
………13分
21.(本题满分14分)
厦门六中高二(下)期中考试数学(理科)试卷
评分标准
20.(本题满分14分)
19.(本题满分13分)
18.(本题满分13分)
17.(本题满分13分)
16.(本题满分13分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com