
33.(朝阳·文·题19)
已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为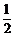 ,且经过点
,且经过点 ,过点
,过点 的直线
的直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 .
.
⑴求椭圆 的方程;
的方程;
⑵是否存直线 ,满足
,满足 ?
? 若存在,求出直线
若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
[解析]
⑴设椭圆 的方程为
的方程为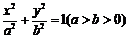 ,
,
由题意得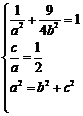
解得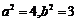 ,
,
故椭圆 的方程为
的方程为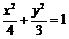 5分
5分
⑵若存在直线 满足条件,设直线
满足条件,设直线 的方程为
的方程为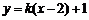
由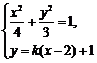
得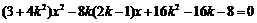
因为直线 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 .
.
设 两点的坐标分别为
两点的坐标分别为
所以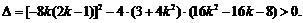
整理,得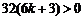
解得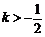 .
.
又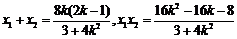
且 .即
.即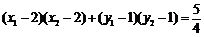 .
.
所以
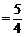
即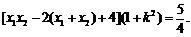
所以
 解得
解得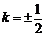 .所以
.所以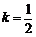 .
.
于是,存在直线 满足条件,其方程为
满足条件,其方程为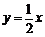 .
.
32.(朝阳·理·题19)
已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为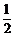 ,且经过点
,且经过点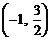 ,过点
,过点 的直线
的直线 与椭圆
与椭圆 在第一象限相切于点
在第一象限相切于点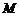 .
.
⑴求椭圆 的方程;
的方程;
⑵求直线 的方程以及点
的方程以及点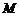 的坐标;
的坐标;
⑶是否存过点 的直线
的直线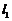 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,满足
,满足 ?若存在,求出直线
?若存在,求出直线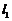 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
[解析]
⑴设椭圆 的方程为
的方程为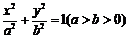 ,由题意得
,由题意得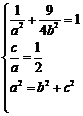
解得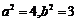 ,故椭圆
,故椭圆 的方程为
的方程为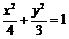 .
.
⑵因为过点 的直线
的直线 与椭圆在第一象限相切,所以
与椭圆在第一象限相切,所以 的斜率存在,故可设直线
的斜率存在,故可设直线 的方程为
的方程为
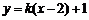 .
.
由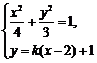
得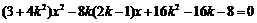 . ①
. ①
因为直线 与椭圆
与椭圆 相切,所以
相切,所以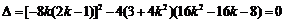 .
.
整理,得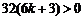 .解得
.解得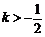 .
.
所以直线 的方程为
的方程为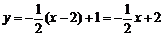 .
.
将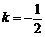 代入①式,可以解得
代入①式,可以解得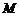 点横坐标为
点横坐标为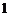 ,故切点
,故切点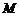 坐标为
坐标为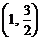 .
.
⑶若存在直线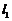 满足条件的方程为
满足条件的方程为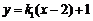 ,代入椭圆
,代入椭圆 的方程得
的方程得
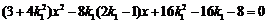 .
.
因为直线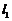 与椭圆
与椭圆 相交于不同的两点
相交于不同的两点 ,设
,设 两点的坐标分别为
两点的坐标分别为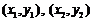 ,
,
所以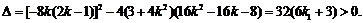
所以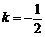 .
.
又 ,
,
因为 ,即
,即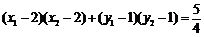 ,
,
所以
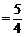 .
.
即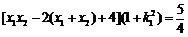 .
.
所以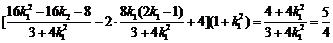 ,解得
,解得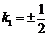 .
.
因为 为不同的两点,所以
为不同的两点,所以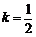 .
.
于是存在直线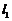 满足条件,其方程为
满足条件,其方程为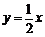 .
.
31.(崇文·文·题19)
已知椭圆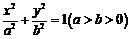 短轴
短轴 的一个端点
的一个端点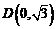 ,离心率
,离心率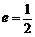 .过
.过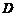 作直线
作直线 与椭圆交于另一点
与椭圆交于另一点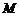 ,与
,与 轴交于点
轴交于点 (不同于原点
(不同于原点 ),点
),点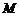 关于
关于 轴的对称点为
轴的对称点为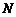 ,直线
,直线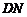 交
交 轴于点
轴于点 .
.
⑴求椭圆的方程;
⑵求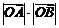 的值.
的值.

[解析]
⑴由已知,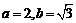 .
.
所以椭圆方程为 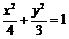 .
.
⑵设直线 方程为
方程为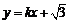 .令
.令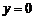 ,得
,得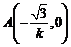 .
.
由方程组 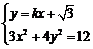 可得
可得 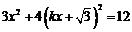 ,即
,即
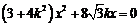 .
.
所以 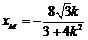 ,
,
所以 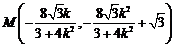 ,
,
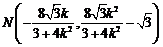 .
.
所以 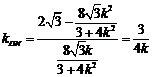 .
.
直线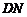 的方程为
的方程为 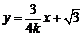 .
.
令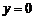 ,得
,得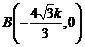 .
.
所以 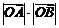 =
= .
.
30.(崇文·理·题19)
已知抛物线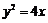 ,点
,点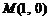 关于
关于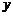 轴的对称点为
轴的对称点为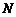 ,直线
,直线 过点
过点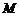 交抛物线于
交抛物线于 两点.
两点.
⑴证明:直线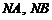 的斜率互为相反数;
的斜率互为相反数;
⑵求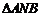 面积的最小值;
面积的最小值;
⑶当点 的坐标为
的坐标为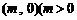 ,且
,且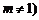 .根据⑴⑵推测并回答下列问题(不必说明理由):
.根据⑴⑵推测并回答下列问题(不必说明理由):
①直线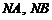 的斜率是否互为相反数?
的斜率是否互为相反数?
② 面积的最小值是多少?
面积的最小值是多少?
[解析]
⑴设直线 的方程为
的方程为 .
.
由 可得
可得 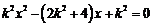 .
.
设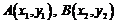 ,则
,则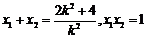 .
.
∴
∴
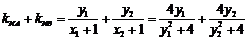
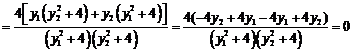 .
.
又当 垂直于
垂直于 轴时,点
轴时,点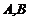 关于
关于 轴,显然
轴,显然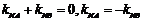 .
.
综上,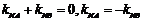 .
---------------- 5分
.
---------------- 5分
⑵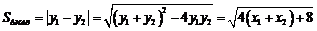 =
= .
.
当 垂直于
垂直于 轴时,
轴时,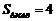 .
.
∴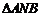 面积的最小值等于
面积的最小值等于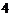 .
----------------10分
.
----------------10分
⑶推测:① ;
;
②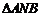 面积的最小值为
面积的最小值为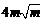 .
.
29.(宣武·文·题19)
已知椭圆的中心在原点 ,焦点在
,焦点在 轴上,点
轴上,点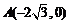 是其左顶点,点
是其左顶点,点 在椭圆上且
在椭圆上且 .
.
⑴求椭圆的方程;
⑵若平行于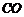 的直线
的直线 和椭圆交于
和椭圆交于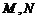 两个不同点,求
两个不同点,求 面积的最大值,并求此时直线
面积的最大值,并求此时直线 的方程.
的方程.
[解析]
⑴设椭圆的标准方程为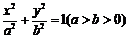 ,
,
∵左顶点 .
.
∴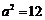 ,
,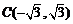
又∵ 在椭圆上,
在椭圆上,
∴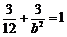 ,
,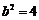
∴椭圆的标准方程为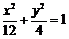 .
.
⑵设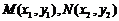
∵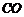 的斜率为
的斜率为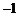 ,∴设直线
,∴设直线 的方程为
的方程为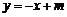 ,
,
代入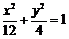 ,得
,得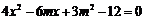 .
.

∴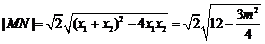
又 到直线
到直线 的距离
的距离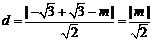 ,
,
∴ 的面积
的面积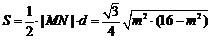
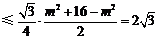 ,
,
当且仅当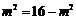 时取等号,此时
时取等号,此时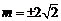 满足题中条件,
满足题中条件,
∴直线 的方程为
的方程为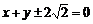 .
.
28.(宣武·理·题19)
已知椭圆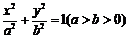 的离心率为
的离心率为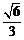 .
.
⑴若原点到直线 的距离为
的距离为 ,求椭圆的方程;
,求椭圆的方程;
⑵设过椭圆的右焦点且倾斜角为 的直线
的直线 和椭圆交于
和椭圆交于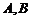 两点.
两点.
i)当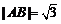 ,求
,求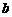 的值;
的值;
ii)对于椭圆上任一点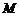 ,若
,若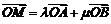 ,求实数
,求实数 满足的关系式.
满足的关系式.
[解析]
⑴∵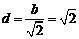 ,∴
,∴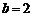 .
.
∵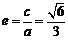 ,∴
,∴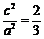 .
.
∵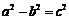 ,∴
,∴ ,解得
,解得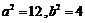 .
.
椭圆的方程为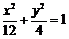 .
.
⑵
i)∵ ,∴
,∴ ,椭圆的方程可化为
,椭圆的方程可化为
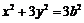 …………①
…………①
易知右焦点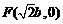 ,据题意有
,据题意有 :
: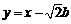 ………②
………②
由①,②有: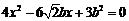 …………③
…………③
设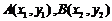 ,
,

∴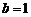
ii)显然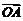 与
与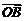 可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量
可作为平面向量的一组基底,由平面向量基本定理,对于这一平面内的向量 ,有且只有一对实数
,有且只有一对实数 ,使得等式
,使得等式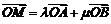 成立.
成立.
设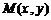 ,
,
∵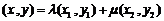 ,∴
,∴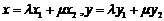
又点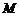 在椭圆上,∴
在椭圆上,∴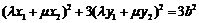 ……………④
……………④
由③有:
则
……………⑤
又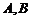 在椭圆上,故有
在椭圆上,故有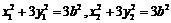 …………⑥
…………⑥
将⑥,⑤代入④可得: .
.
27.(东城·文·题19)
已知椭圆 :
: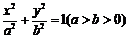 的离心率为
的离心率为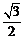 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线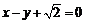 相切.
相切.
⑴求椭圆C的方程;
⑵设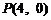 ,
,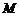 、
、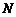 是椭圆
是椭圆 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结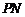 交椭圆
交椭圆 于另一点
于另一点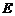 ,求直线
,求直线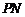 的斜率的取值范围;
的斜率的取值范围;
⑶在⑵的条件下,证明直线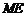 与
与 轴相交于定点.
轴相交于定点.
[解析]
⑴由题意知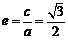 ,
,
所以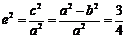 ,即
,即 ,
,
又因为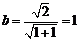 ,所以
,所以 ,
,
故椭圆 的方程为
的方程为 :
: .
.
⑵由题意知直线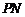 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为 ①
①
联立 消去
消去 得:
得: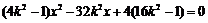 ,
,
由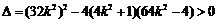 得
得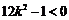 ,
,
又 不合题意,
不合题意,
所以直线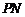 的斜率的取值范围是
的斜率的取值范围是 或
或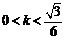 .
.
⑶设点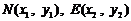 ,则
,则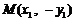 ,
,
直线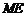 的方程为
的方程为 ,
,
令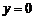 ,得
,得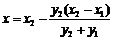 ,
,
将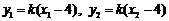 代入整理,得
代入整理,得 . ②
. ②
由得①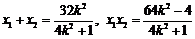 代入②整理,得
代入②整理,得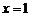 ,
,
所以直线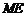 与
与 轴相交于定点
轴相交于定点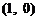 .
.
26.(东城·理·题19)
已知椭圆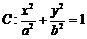
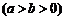 的离心率为
的离心率为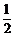 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线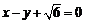 相切.
相切.
⑴求椭圆 的方程;
的方程;
⑵设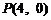 ,
, ,
, 是椭圆
是椭圆 上关于
上关于 轴对称的任意两个不同的点,连结
轴对称的任意两个不同的点,连结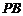 交椭圆
交椭圆 于另一点
于另一点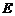 ,证明直线
,证明直线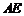 与
与 轴相交于定点
轴相交于定点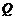 ;
;
⑶在⑵的条件下,过点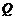 的直线与椭圆
的直线与椭圆 交于
交于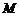 ,
,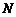 两点,求
两点,求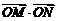 的取值范围.
的取值范围.
[解析]
⑴由题意知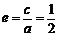 ,所以
,所以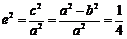 .即
.即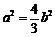 .
.
又因为 ,所以
,所以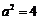 ,
, .
.
故椭圆 的方程为
的方程为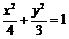 .
.
⑵由题意知直线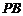 的斜率存在,设直线
的斜率存在,设直线 的方程为
的方程为 .
.
由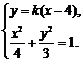 得
得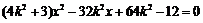 . ①
. ①
设点 ,
, ,则
,则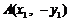 .
.
直线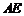 的方程为
的方程为 .
.
令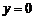 ,得
,得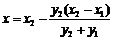 .
.
将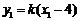 ,
,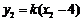 代入整理,得
代入整理,得 .②
.②
由①得 ,
,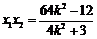 代入②整理,得
代入②整理,得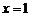 .
.
所以直线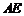 与
与 轴相交于定点
轴相交于定点 .
.
⑶当过点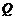 直线
直线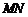 的斜率存在时,
的斜率存在时,
设直线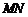 的方程为
的方程为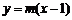 ,且
,且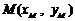 ,
, 在椭圆
在椭圆 上.
上.
由 得
得 .
.
易知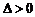 .
.
所以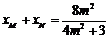 ,
,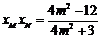 ,
,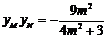 .
.
则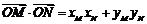
 .
.
因为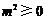 ,所以
,所以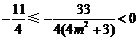 .
.
所以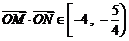 .
.
当过点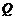 直线
直线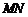 的斜率不存在时,其方程为
的斜率不存在时,其方程为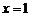 .
.
解得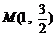 ,
,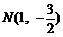 .此时
.此时 .
.
所以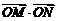 的取值范围是
的取值范围是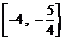 .
.
25.(西城·文·题18)
椭圆 :
: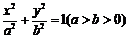 的离心率为
的离心率为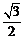 ,且过
,且过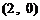 点.
点.
⑴求椭圆 的方程;
的方程;
⑵设直线 :
: 与椭圆
与椭圆 交于
交于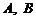 两点,
两点, 为坐标原点,若
为坐标原点,若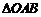 直角三角形,
直角三角形, 求
求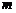 的值.
的值.
[解析]
⑴已知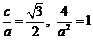 ,
,
所以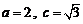 ,又
,又 ,所以
,所以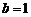 ,
,
所以椭圆C的方程为 .
.
⑵联立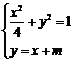 ,消去y得
,消去y得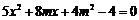 ,
,
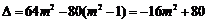 ,
,
令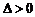 ,即
,即 ,解得
,解得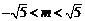 .
.
设A,B两点的坐标分别为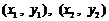 ,
,
i)当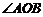 为直角时,则
为直角时,则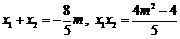 ,
,
因为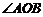 为直角,所以
为直角,所以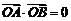 ,即
,即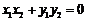 ,
,
所以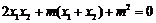 ,
,
所以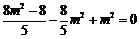 ,解得
,解得 ;
;
ii)当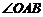 或
或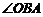 为直角时,不妨设
为直角时,不妨设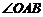 为直角,
为直角,
由直线 的斜率为
的斜率为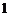 ,可得直线
,可得直线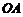 的斜率为
的斜率为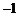 ,
,
所以 ,即
,即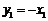 ,
,
又 ,所以
,所以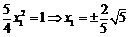 .
.
 ,
,
依题意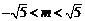 ,且
,且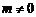 ,
,
经检验,所求 值均符合题意,综上,
值均符合题意,综上, 的值为
的值为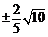 和
和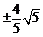 .
.
24.(西城·理·题18)
椭圆 :
: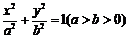 的离心率为
的离心率为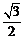 ,长轴端点与短轴端点间的距离为
,长轴端点与短轴端点间的距离为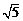 .
.
⑴求椭圆 的方程;
的方程;
⑵设过点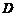
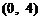
 的直线
的直线 与椭圆
与椭圆 交于
交于 两点,
两点, 为坐标原点,若
为坐标原点,若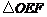 为直角三角形,求直线
为直角三角形,求直线 的斜率.
的斜率.
[解析]
⑴由已知 ,
,
又 ,解得
,解得 ,
,
所以椭圆 的方程为
的方程为 ;
;
⑵根据题意,过点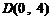 满足题意的直线斜率存在,设
满足题意的直线斜率存在,设 ,
,
联立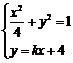 ,消去y得
,消去y得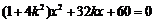 ,
,
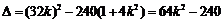 ,
,
令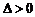 ,解得
,解得 .
.
设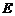 、
、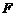 两点的坐标分别为
两点的坐标分别为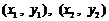 ,
,
ⅰ)当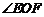 为直角时,
为直角时,
则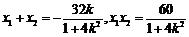 ,
,
因为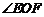 为直角,所以
为直角,所以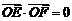 ,即
,即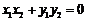 ,
,
所以 ,
,
所以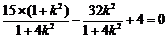 ,解得
,解得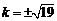 .
.
ⅱ)当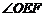 或
或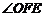 为直角时,不妨设
为直角时,不妨设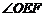 为直角,
为直角,
此时,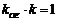 ,所以
,所以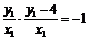 ,即
,即 ……①
……①
又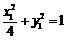 …………②
…………②
将①代入②,消去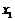 得
得 ,
,
解得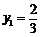 或
或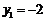 (舍去),
(舍去),
将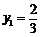 代入①,得
代入①,得 所以
所以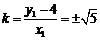 ,
,
经检验,所求k值均符合题意,综上,k的值为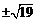 和
和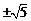 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com