
1、①以乱易整 ②以其无礼于晋 ③焉用亡郑以陪邻 ④若舍郑以为东道主 ⑤越国以鄙远,君知其难也
( )和( )相同
《 左传》又名《 》《 》,是我国最早最完备的编年体史书。与《 》《 》被称为“春秋三传”。
23.(本题满分10分)坐标系与参数方程选做题
在直角坐标系xoy中,以o为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为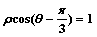 ,M,N分别为C与x轴,y轴的交点
,M,N分别为C与x轴,y轴的交点
(1)写出C的直角坐标方程,并求出M,N的极坐标;
(2)设MN的中点为P,求直线OP的极坐标方程.
22.(本题满分10分)不等式选讲选做题
设函数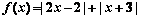 .
.
(1)解不等式 ;
;
(2)若关于的不等式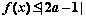 的解集不是空集,试求
的解集不是空集,试求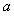 的取值范围.
的取值范围.
21.(本题满分12分)
已知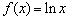 ,
,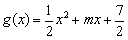 (
(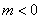 ),直线
),直线 与函数
与函数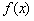 、
、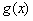 的图像都相切,且与函数
的图像都相切,且与函数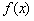 的图像的切点的横坐标为1.
的图像的切点的横坐标为1.
(Ⅰ)求直线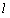 的方程及
的方程及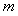 的值;
的值;
(Ⅱ)若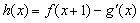 (其中
(其中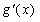 是
是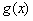 的导函数),求函数
的导函数),求函数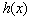 的最大值;
的最大值;
(Ⅲ)当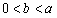 时,求证:
时,求证: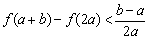 .
.
请考生在第22,23两题中任选一题做答,写出必要解答过程,如果多做,则按所做的第一题计分
20.(本题满分12分)
一束光线从点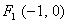 出发,经直线
出发,经直线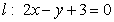 上一点
上一点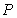 反射后,恰好穿过点
反射后,恰好穿过点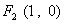 .
.
(Ⅰ)求点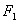 关于直线
关于直线 的对称点
的对称点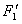 的坐标;
的坐标;
(Ⅱ)求以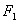 、
、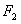 为焦点且过点
为焦点且过点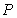 的椭圆
的椭圆 的方程;
的方程;
(Ⅲ)设直线 与椭圆
与椭圆 的两条准线分别交于
的两条准线分别交于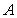 、
、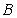 两点,点
两点,点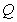 为线段
为线段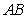 上的动点,求点
上的动点,求点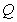 到
到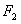 的距离与到椭圆
的距离与到椭圆 右准线的距离之比的最小值,并求取得最小值时点
右准线的距离之比的最小值,并求取得最小值时点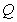 的坐标.
的坐标.
19. (本题满分12分)
(本题满分12分)
已知四棱锥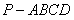 的底面
的底面 是正方形,且
是正方形,且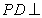 底面
底面 ,其中
,其中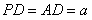 .
.
(1)求二面角 的大小;
的大小;
(2)在线段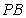 上是否存在一点
上是否存在一点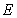 ,使
,使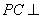 平面
平面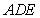 .若存在,
.若存在,
试确定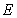 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.
18.(本题满分12分)
已知函数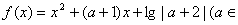 R,且
R,且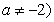 .
.
(I)若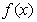 能表示成一个奇函数
能表示成一个奇函数 和一个偶函数
和一个偶函数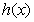 的和,求
的和,求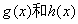 的解析式;
的解析式;
(II)命题P:函数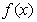 在区间
在区间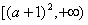 上是增函数;命题Q:函数
上是增函数;命题Q:函数 是减函数.
是减函数.
如果命题P、Q有且仅有一个是真命题,求a的取值范围;
(III)在(II)的条件下,比较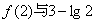 的大小.
的大小.

17.(本题满分12分)
已知函数f(x)在定义域(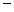
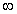 ,1]上是减函数,问是否存在实数k,使不等式f(k
,1]上是减函数,问是否存在实数k,使不等式f(k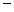 sinx)
sinx)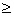 f(k2
f(k2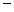 sin2x)对一切实数x恒成立?并说明理由.
sin2x)对一切实数x恒成立?并说明理由.






16. 已知函数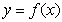 和
和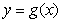 在
在 的图象如下所示:
的图象如下所示:
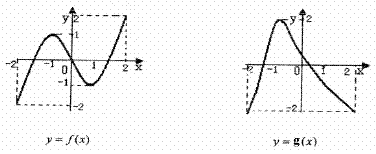

给出下列四个命题:
①方程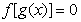 有且仅有6个根 ②方程
有且仅有6个根 ②方程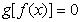 有且仅有3个根
有且仅有3个根
③方程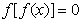 有且仅有5个根 ④方程
有且仅有5个根 ④方程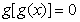 有且仅有4个根
有且仅有4个根
其中正确的命题是 .(将所有正确的命题序号填在横线上). 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com