
21.(本小题满分14分)
设函数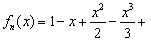 …
…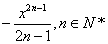
(1)研究函数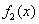 的单调性;
的单调性;
(广东省2010届高三六校第二次联考
20.(本小题满分14分)
已知函数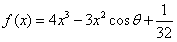 ,其中
,其中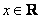 ,
,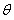 为参数,且
为参数,且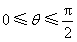 .
.
(1)当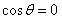 时,判断函数
时,判断函数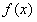 是否有极值;
是否有极值;
(2)要使函数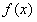 的极小值大于零,求参数
的极小值大于零,求参数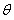 的取值范围;
的取值范围;
(3)若对(Ⅱ)中所求的取值范围内的任意参数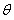 ,函数
,函数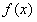 在区间
在区间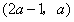 内都是增函数,求实数
内都是增函数,求实数 的取值范围.
的取值范围.
19.(本小题满分14分)
某分公司经销某种品牌产品,每件产品的成本为3元,并且每件产品需向总公司交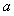 元(
元(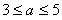 )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为 元(
元(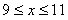 )时,一年的销售量为
)时,一年的销售量为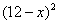 万件.
万件.
(1)求分公司一年的利润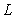 (万元)与每件产品的售价
(万元)与每件产品的售价 的函数关系式;
的函数关系式;
(2)当每件产品的售价为多少元时,分公司一年的利润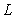 最大,并求出
最大,并求出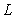 的最大值
的最大值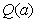 .
.
18.(本小题满分14分)
已知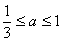 ,若
,若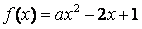 在区间
在区间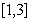 上的最大值为
上的最大值为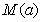 ,最小值为
,最小值为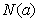 ,令
,令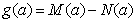 .
.
(1)求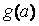 的函数表达式;
的函数表达式;
(2)判断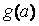 的单调性,并求出
的单调性,并求出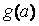 的最小值.
的最小值.
17.(本小题满分12分)
数列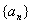 的前
的前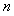 项和为
项和为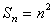 ,数列
,数列 满足
满足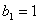 ,且
,且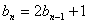 ,
,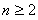 .
.
(1)求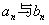 的表达式;
的表达式;
(2)设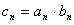 ,求数列
,求数列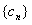 的前
的前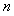 项和
项和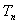 .
.
16.(本小题满分12分)
已知向量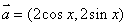 ,
,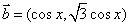 ,函数
,函数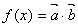 .
.
(1)求函数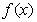 的最小正周期和值域;
的最小正周期和值域;
(2)在
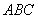 中,
中,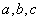 分别是角
分别是角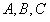 的对边,且
的对边,且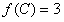 ,
,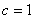 ,
,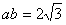 ,且
,且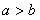 ,求
,求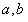 的值.
的值.
(二)选做题(14-15题,考生只能从中选做一题)
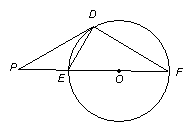
14.(几何证明选讲)如图,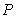 是圆
是圆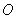 外的一点,
外的一点,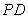 为切线,
为切线,
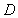 为切点,割线
为切点,割线 经过圆心
经过圆心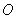 ,
,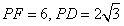 ,
,
则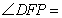 __________.
__________.
15.(坐标系与参数方程选做题)已知曲线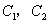 的极坐标方程分别为
的极坐标方程分别为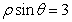 ,
, ,则曲线
,则曲线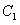 与
与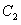 交点的极坐标为
.
交点的极坐标为
.
(一)必做题(11-13题)
11.已知数列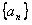 为等差数列,且
为等差数列,且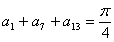 ,则
,则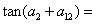 ____________.
____________.
12.设曲线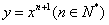 在点(1,1)处的切线与
在点(1,1)处的切线与 轴的交点的横坐标为
轴的交点的横坐标为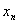 ,令
,令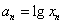 ,则
,则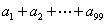 的值为____________.
的值为____________.
13.若定义在区间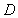 上的函数
上的函数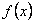 对
对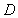 上的任意
上的任意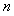 个值
个值 ,
, ,…,
,…,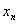 ,总满足
,总满足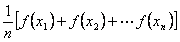 ≤
≤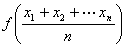 ,则称
,则称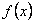 为
为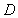 上的凸函数.已知函数
上的凸函数.已知函数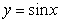 在区间
在区间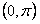 上是“凸函数”,则在△
上是“凸函数”,则在△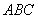 中,
中,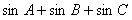 的最大值是____________.
的最大值是____________.
10.在正整数数列中,由1开始依次按如下规则将某些数染成红色.先染1,再染2个偶数2、4;再染4后面最邻近的3个连续奇数5、7、9;再染9后面最邻近的4个连续偶数10、12、14、16;再染16后面最邻近的5个连续奇数17、19、21、23、25.按此规则一直染下去,得到一红色子数列1,2,4,5,7,9,10,12,14,16,17,….则在这个红色子数列中,由1开始的第2009个数是
A.3948 B.3953 C.3955 D.3958
9.如图,Rt△ABC中,AC⊥BC,D在边AC上,已知BC=2,CD=1,∠ABD=45°,则AD=
A.2 B.5 C.4 D.1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com