
31.(宣武·文·题15)
已知函数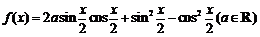
⑴当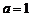 时,求函数
时,求函数 的最小正周期及图象的对称轴方程式;
的最小正周期及图象的对称轴方程式;
⑵当 时,在
时,在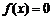 的条件下,求
的条件下,求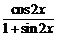 的值.
的值.
[解析]
⑴
最小正周期为 ,
,
由 ,得
,得
⑵当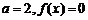 时,解得
时,解得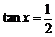 ,
,
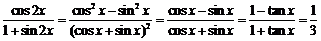 .
.
30.(宣武·理·题15)
已知函数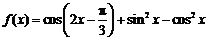
⑴求函数 的最小正周期及图象的对称轴方程;
的最小正周期及图象的对称轴方程;
⑵设函数 ,求
,求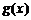 的值域.
的值域.
[解析]
⑴
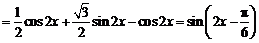 ,
,
∴最小正周期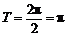 .
.
由 ,得
,得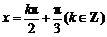
函数图象的对称轴方程为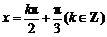
⑵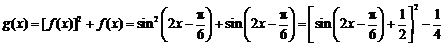
当 时,
时,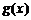 取得最小值
取得最小值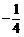 ;
;
当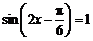 时,
时,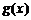 取得最大值2,
取得最大值2,
所以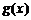 的值域为
的值域为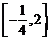 .
.
29.(东城·理·题15)(东城·文·题15)
设函数 .
.
⑴求 的最小正周期;
的最小正周期;
⑵当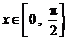 时,求函数
时,求函数 的最大值和最小值.
的最大值和最小值.
[解析]


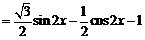
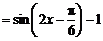 .
.
⑴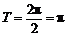 ,故
,故 的最小正周期为
的最小正周期为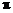 .
.
⑵因为 ,
,
所以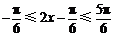 .
.
所以当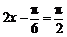 ,即
,即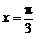 时,
时, 有最大值
有最大值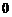 ,
,
当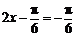 ,即
,即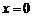 时,
时, 有最小值
有最小值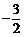 .
.
28.(西城·理·题15)(西城·文·题16)
已知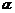 为锐角,且
为锐角,且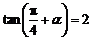 .
.
⑴求 的值;
的值;
⑵求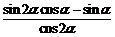 的值.
的值.
[解析]
⑴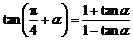 ,
,
所以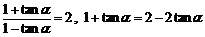 ,所以
,所以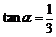 .
.
⑵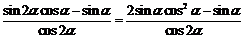
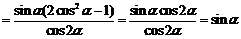 .
.
因为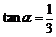 ,所以
,所以 ,又
,又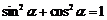 ,
,
所以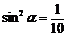 ,
,
又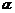 为锐角,所以
为锐角,所以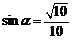 ,
,
所以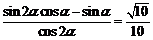 .
.
27.(石景山·理·题15)(石景山·文·题15)
在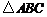 中,角
中,角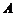 ,
, ,
, 所对的边分别为
所对的边分别为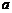 ,
,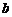 ,
,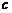 ,且
,且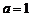 ,
,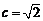 ,
, .
.
⑴求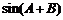 的值;
的值;
⑵求 的值;
的值;
⑶求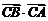 的值.
的值.
[解析]
⑴∵在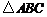 中,
中,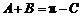 ,
,
∴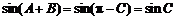 .
.
又∵ ,∴
,∴ 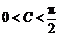 ,∴
,∴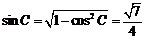 .
.
∴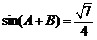 .
.
⑵由正弦定理得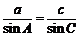 ,
,
∴ .
.
⑶由余弦定理得 ,
,
∴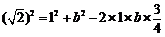 ,即
,即 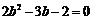 .
.
解得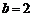 或
或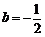 (舍).
(舍).
∴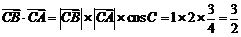 .
.
26.(丰台·理科·题15)(丰台·文科·题15)
已知函数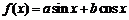 的图象经过点
的图象经过点 ,
,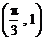 .
.
⑴求实数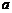 、
、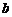 的值;
的值;
⑵若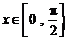 ,求函数
,求函数 的最大值及此时
的最大值及此时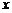 的值.
的值.
[解析]
⑴∵函数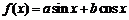 的图象经过点
的图象经过点 ,
,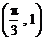 ,
,
∴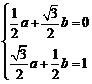
解得: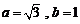
⑵由⑴知: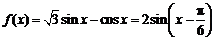
∵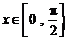 ,∴
,∴
∴当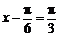 ,即
,即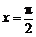 时,
时, 取得最大值
取得最大值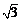 .
.
25.(海淀·文科·题15)
已知函数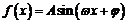 ,
,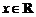 (其中
(其中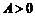 ,
,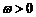 ,
,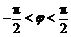 ),其部分图象如图所示.
),其部分图象如图所示.

⑴求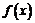 的解析式;
的解析式;
⑵求函数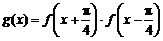 在区间
在区间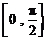 上的最大值及相应的
上的最大值及相应的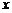 值.
值.
[解析]
⑴由图可知,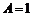 ,
,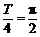 ,所以
,所以
∴
又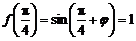 ,且
,且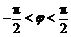 ,所以
,所以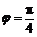
所以 .
.
⑵由⑴ ,
,
所以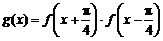 =
=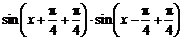
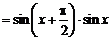

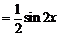
因为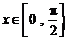 ,所以
,所以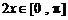 ,
,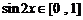 .
.
故 ,当
,当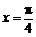 时,
时,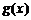 取得最大值
取得最大值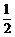 .
.
24.(海淀·理科·题15)
已知函数 的图象如图所示.
的图象如图所示.
⑴求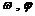 的值;
的值;
⑵设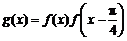 ,求函数
,求函数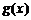 的单调递增区间.
的单调递增区间.

[解析]
⑴由图可知 ,
,
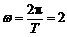 ,
,
又由 得
得 ,又
,又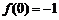 ,得
,得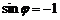
∵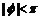 ,∴
,∴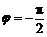 ,
,
⑵由⑴知: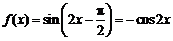
因为
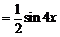
所以,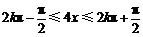 ,即
,即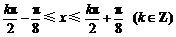 .
.
故函数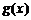 的单调增区间为
的单调增区间为 .
.
23.(朝阳·文·题9)
函数 的最大值是
.
的最大值是
.
[解析]
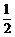 ;
;
 .于是当
.于是当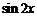 取最大值1时,
取最大值1时, 有最大值
有最大值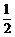 .
.
22.(朝阳·文·题4)
下列函数中,最小正周期为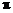 ,且图象关于直线
,且图象关于直线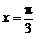 对称的是 ( )
对称的是 ( )
A.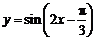 B.
B.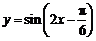
C.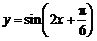 D.
D.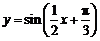
[解析] B;
对于A,C,直线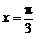 不是其对称轴;对于D,其最小正周期为
不是其对称轴;对于D,其最小正周期为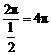 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com