
22. (宣武·文·题20)
数列 的前
的前 项和
项和 为
为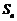 ,若
,若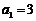 ,点
,点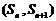 在直线
在直线 上.
上.
⑴求证:数列 是等差数列;
是等差数列;
⑵若数列 满足
满足
 ,求数列
,求数列 的前
的前 项和
项和 ;
;
⑶设 ,求证:
,求证: .
.
[解析]
⑴∵点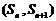 在直线
在直线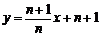
 上,
上,
∴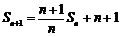 .
.
两边同除以 ,得
,得 ,
,
于是 是以
是以 为首项,
为首项, 为公差的等差数列.
为公差的等差数列.
⑵由⑴可知, ,即
,即 ,
,
∴当 时,
时,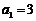 ,
,
当 时,
时,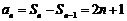 ,
,
经检验,当 时也成立,∴
时也成立,∴ .
.
于是 .
.
∵ ,
,
∴ ,
,
相减,解得: .
.
⑶∵ ,
,
∴
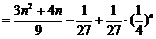
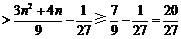 .
.
21. (西城·理·题20)
对于各项均为整数的数列 ,如果
,如果 (
( =1,2,3,…)为完全平方数,则称数列
=1,2,3,…)为完全平方数,则称数列 具有“
具有“ 性质”.
性质”.
不论数列 是否
是否 具有“
具有“ 性质”,如果存在与
性质”,如果存在与 不是同一数列的
不是同一数列的 ,且
,且 同时满足下面两个条件:①
同时满足下面两个条件:① 是
是 的一个排列;②数列
的一个排列;②数列 具有“
具有“ 性质”,则称数列
性质”,则称数列 具有“变换
具有“变换 性质”.
性质”.
⑴设数列 的前
的前 项和
项和 ,证明数列
,证明数列 具有“
具有“ 性质”;
性质”;
⑵试判断数列1,2,3,4,5和数列1,2,3,…,11是否具有“变换 性质”,具有此性质的数列请写出相应的数列
性质”,具有此性质的数列请写出相应的数列 ,不具此性质的说明理由;
,不具此性质的说明理由;
⑶对于有限项数列 :1,2,3,…,
:1,2,3,…, ,某人已经验证当
,某人已经验证当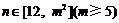 时,数列
时,数列 具有“变换
具有“变换 性质”,试证明:当”
性质”,试证明:当” 时,数
时,数 列
列 也具有“变换
也具有“变换 性质”.
性质”.
[解析]
⑴当 时,
时,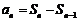
 ,
,
又 ,所以
,所以 .
.
所以 是完全平方数,数列
是完全平方数,数列 具有“
具有“ 性质”;
性质”;
⑵数列1,2,3,4,5具有“变换 性质”,
性质”,
数列 为3,2,1,5,4,
为3,2,1,5,4,
数列1,2,3,…,11不具有“变换 性质”,
性质”,
因为11,4都只有与5的和才能构成完全平方数,
所以数列1,2,3,…,11不具有“变换 性质”;
性质”;
⑶设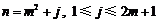 ,
,
注意到 ,
,
令 ,
,
由于 ,
,
所以 ,
,
又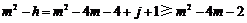 ,
, ,
,
所以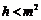 ,即
,即 ,
,
因为当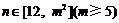 时,数列
时,数列 具有“变换
具有“变换 性质”,
性质”,
所以1,2,…, 可以排列成
可以排列成 ,
,
使得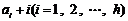 都是平方数.
都是平方数.
另外, 可以按相反顺序排列,
可以按相反顺序排列,
即排列为 ,
,
使得 ,
,
所以1,2, 可以排列成
可以排列成
 ,
,
满足 都是平方数.
都是平方数.
即当 时,数列
时,数列 也具有“变换
也具有“变换 性质”.
性质”.
20. (东城·理·题20)
已知数列 满足
满足 ,
, .
.
⑴求证: ;
;
⑵求证: ;
;
⑶求数列 的通项公式.
的通项公式.
[解析] ⑴用数学归纳法证明
ⅰ)当 时,
时,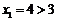 .所以结论成立.
.所以结论成立.
ⅱ)假设 时结论成立,即
时结论成立,即 ,则
,则 .
.
所以 .
.
即 时,结论成立.
时,结论成立.
由ⅰ)、ⅱ)可知对任意的正整数 ,都有
,都有 .
.
⑵ .
.
因为 ,所以
,所以 ,即
,即 .
.
所以 .
.
⑶ ,
, ,
,
所以 .
.
又 ,所以
,所以 .
.
又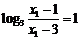 ,令
,令 ,
,
则数列 是首项为
是首项为 ,公比为
,公比为 的等比数列.所以
的等比数列.所以 .
.
由 ,得
,得 .
.
所以 .
.
19. (东城·文·题20)
已知数列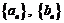 ,其中
,其中 ,数列
,数列 的前
的前 项和
项和 ,数列
,数列 满足
满足 .
.
⑴求数列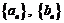 的通项公式;
的通项公式;
⑵是否存在自然数 ,使得对于任意
,使得对于任意 ,
, ,有
,有 恒成立?若存在,求出
恒成立?若存在,求出 的最小值;
的最小值;
⑶若数列 满足
满足 ,求数列
,求数列 的前
的前 项和
项和 .
.
[解析]
⑴因为 .
.
当 时,
时, ;
;
所以 .
.
所以 .即
.即 .
.
又 ,
,
所以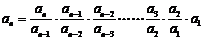
 .
.
当 时,上式成立.
时,上式成立.
因为 ,
,
所以 是首项为
是首项为 ,公比为
,公比为 的等比数列,故
的等比数列,故 ;
;
⑵由⑴知, .
.
则 ,
,
假设存在自然数 ,使得对于任意
,使得对于任意 ,有
,有 恒成立,
恒成立,
即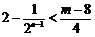 恒成立,由
恒成立,由 ,解得
,解得 ,
,
所以存在自然数 ,使得对于任意
,使得对于任意 ,
,
有 恒成立,此时,
恒成立,此时, 的最小值为16.
的最小值为16.
⑶当 为奇数时,
为奇数时,
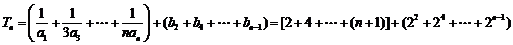
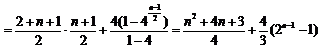 ;
;
当 为偶数时,
为偶数时,

 ;
;
因此 .
.
18. (海淀·理·题20)
已知数列 满足:
满足: ,
, ,
, .
.
⑴求 的值;
的值;
⑵设 ,试求数列
,试求数列 的通项公式;
的通项公式;
⑶对于任意的正整数 ,试讨论
,试讨论 与
与 的大小关系.
的大小关系.
[解析]
⑴∵ ,
, ,
, ,
, ,
,
∴ ;
; ;
; .
.
⑵由题设,对于任意的正整数 ,都有:
,都有:
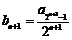

 ,
,
∴ .
.
∴数列 是以
是以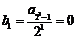 为首项,
为首项, 为公差的等差数列.
为公差的等差数列.
∴ .
.
⑶对于任意的正整数 ,
,
当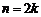 或
或 时,
时, ;
;
当 时,
时, ;
;
当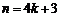 时,
时, .
.
证明如下:
首先,由 ,
,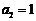 ,
, ,
, 可知
可知 时,
时, ;
;
其次,对于任意的正整数 ,
,
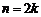 时,
时,

 ;
;
 时,
时,




所以 .
.
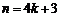 时,
时,




事实上,我们可以证明:对于任意正整数 ,
, …(*)(证明见后),
…(*)(证明见后),
所以此时 .
.
综上可知:结论得证.
对于任意正整数 ,
, (*)的证明如下:
(*)的证明如下:
ⅰ)当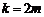 (
( )时,
)时,
 ,满足(*)式.
,满足(*)式.
ⅱ)当 时,
时, ,满足(*)式.
,满足(*)式.
ⅲ)当 时,
时,



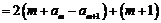
于是只须证明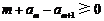 ,如此递推,可归结为ⅰ)或ⅱ)的情形,
,如此递推,可归结为ⅰ)或ⅱ)的情形,
于是(*)得证.
17. (海淀·文·题20)
已知数列 满足:
满足: ,
, ,
, .
.
⑴求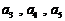 的值;
的值;
⑵设 ,
, ,求证:数列
,求证:数列 是等比数列,并求出其通项公式;
是等比数列,并求出其通项公式;
⑶对任意的 ,
, ,在数列
,在数列 中是否存在连续的
中是否存在连续的 项构成等差数列?若存在,写出这
项构成等差数列?若存在,写出这 项,并证明这
项,并证明这 项构成等差数列;若不存在,说明理由.
项构成等差数列;若不存在,说明理由.
[解析]
⑴因为 ,所以
,所以 ,
, ,
,
 ,
, ;
;
⑵由题意,对于任意的正整数 ,
, ,所以
,所以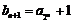
又 所以
所以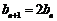 .
.
又
所以 是首项为
是首项为 ,公比为
,公比为 的等比数列,所以
的等比数列,所以
⑶存在.事实上, 对任意的
对任意的 ,
, ,在数列
,在数列 中,
中,
 这连续的
这连续的 项就构成一个等差数列
项就构成一个等差数列
我们先来证明:
“对任意的 ,
, ,
,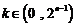 ,
, ,有
,有 ”
”
由⑵得 ,所以
,所以 .
.
当 为奇数时,
为奇数时,
当 为偶数时,
为偶数时,
记
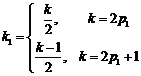 ,其中
,其中 .
.
因此要证 ,只需证明
,只需证明 ,
,
其中 ,
,
(这是因为若 ,则当
,则当 时,则
时,则 一定是奇数,
一定是奇数,
有
= ;
;
当 时,则
时,则 一定是偶数,有
一定是偶数,有
= )
)
如此递推,要证 , 只要证
, 只要证 明
明 ,
,
其中 ,其中
,其中 .,
., ,
,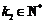
如此递推下去,我们只需证明 ,
, ,
,
即 ,即
,即 ,由(I)可得,
,由(I)可得,
所以对 ,
, ,
,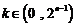 ,
, ,有
,有 ,
,
对任意的 ,
, ,
,
 ,
,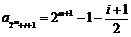 ,其中
,其中 ,
, ,
,
所以
又 ,
, ,所以
,所以
所以 这连续的
这连续的 项,
项,
是首项为 ,公差为
,公差为 的等差数列.
的等差数列.
说明:当 (其中
(其中 ,
,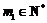 ,
, )时,
)时,
因为 构成一个项数为
构成一个项数为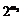 的等差数列,所以从这个数列中任取连续的
的等差数列,所以从这个数列中任取连续的 项,也是一个项数为
项,也是一个项数为 ,公差为
,公差为 的等差数列.
的等差数列.
16. (丰台·理·题20)
设集合 由满足下列两个条件的数列
由满足下列两个条件的数列 构成:
构成:
①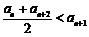 ;
;
②存在实数 ,使
,使 .(
.( 为正整数)
为正整数)
⑴在只有 项的有限数列
项的有限数列 ,
, 中,其中
中,其中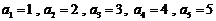 ;
;
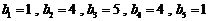 ;试判断数列
;试判断数列 是否为集合
是否为集合 的元素;
的元素;
⑵设 是各项为正的等比数列,
是各项为正的等比数列,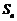 是其前
是其前 项和,
项和,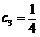 ,
,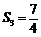 ,
,
证 明数列
明数列 ;并写出
;并写出 的取值范围;
的取值范围;
⑶设数列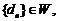 且对满足条件的
且对满足条件的 的最小值
的最小值 ,都有
,都有 .
.
求证:数列 单调递增.
单调递增.
[解析]
⑴对于数列 ,取
,取 ,显然不满足集合
,显然不满足集合 的条件,①
的条件,①
故 不是集合
不是集合 中的元素,
中的元素,
对于数列 ,当
,当 时,
时,
不仅有 ,
, ,
, ,而且有
,而且有 ,
,
显然满足集合 的条件①②,
的条件①②,
故 是集合
是集合 中的元素.
中的元素.
⑵∵ 是各项为正数的等比数列,
是各项为正数的等比数列,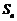 是其前
是其前 项和,
项和,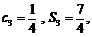
设其公比为 ,
,
∴ ,整理得
,整理得 .
.
∴ ,∴
,∴ ,
,
对于 ,有
,有 ,且
,且 ,
,
故 ,且
,且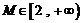
⑶证明:(反证)若数列 非单调递增,则一定存在正整数
非单调递增,则一定存在正整数 ,
,
使 ,易证于任意的
,易证于任意的 ,都有
,都有 ,证明如下:
,证明如下:
假设 时,
时,
当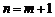 时,由
时,由 ,
, .
.
而
所以
所以对于任意的 ,都有
,都有 .
.
显然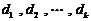 这
这 项中有一定存在一个最大值,不妨记为
项中有一定存在一个最大值,不妨记为 ;
;
所以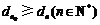 ,从而
,从而 与这题矛盾.
与这题矛盾.
所以假设不成立,故命题得证.
15. (丰台·文·题20)
设集合 由满足下列两个条件的数列
由满足下列两个条件的数列 构成:
构成:
①
②存在实数 ,使
,使 .(
.( 为正整数)
为正整数)
⑴在只有 项的有限数列
项的有限数列 ,
, 中,其中
中,其中 ,
, ,
, ,
, ,
, ,
,
 ,
, ,
, ,
,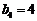 ,
, ;试判断数列
;试判断数列 ,
, 是否为集合
是否为集合 的元素;
的元素;
⑵设 是等差数列,
是等差数列,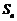 是其前
是其前 项和,
项和, ,
,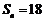 证明数列
证明数列 ;并写出
;并写出 的取值范围;
的取值范围;
⑶设数列 ,且对满足条件的常数
,且对满足条件的常数 ,存在正整数
,存在正整数 ,使
,使 .
.
求证: .
.
[解析]
⑴对于数列 ,当
,当 时,
时, ,显然不满足集合
,显然不满足集合 的条件①,
的条件①,
故 不是集合
不是集合 中的元素,
中的元素,
对于数列 ,当
,当 时,
时,
不仅有 ,
, ,
, ,而且有
,而且有 ,
,
显然满足集合 的条件①②,
的条件①②,
故 是集合
是集合 中的元素.
中的元素.
⑵∵ 是等差数列,
是等差数列,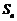 是其前
是其前 项和,
项和,
 ,
, .设其公差为
.设其公差为 ,∴
,∴ .
.
∴
∴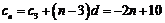 ,
,
∵ ,∴
,∴ .
.
∵ ,∴
,∴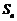 的最大值是
的最大值是 ,即
,即 .
.
∴
 ,且
,且 的取值范围是
的取值范围是 .
.
⑶证明:∵ ,∴
,∴ .
.
整理 ,
,
∵ ,∴
,∴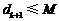 ,∴
,∴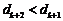 .
.
又∵ ,∴
,∴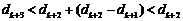 ,
,
∴ .
.
14. (西城·文·题19)
设数列 为等比数列,数列
为等比数列,数列 满足
满足 ,
, ,已知
,已知 ,
, ,其中
,其中 .
.
⑴求数列 的首项和公比;
的首项和公比;
⑵当 时,求
时,求 ;
;
⑶设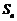 为数列
为数列 的前
的前 项和,若对于任意的正整数
项和,若对于任意的正整数 ,都有
,都有 ,求实数
,求实数 的取值范围.
的取值范围.
[解析]
⑴由已知 ,所以
,所以 ;
;
 ,所以
,所以 ,解得
,解得 ;
;
所以数列 的公比
的公比 ;
;
⑵当 时,
时, ,
,
 ,………………………①,
,………………………①,
 ,……………………②,
,……………………②,
②-①得 ,
,
所以 ,
,
 .
.
⑶ ,
,
因为 ,所以由
,所以由 得
得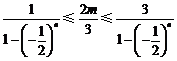 ,
,
注意到,当n为奇数时, ;当
;当 为偶数时,
为偶数时, ,
,
所以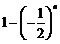 最大值为
最大值为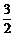 ,最小值为
,最小值为 .
.
对于任意的正整数n都有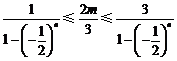 ,
,
所以 ,解得
,解得 ,
,
即所求实数m的取值范围是 .
.
13. (石景山·理·题18)
在数列 中,
中,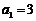 ,
,
 且
且 .
.
⑴求 ,
, 的值;
的值;
⑵证明:数列 是等比数列,并求
是等比数列,并求 的通项公式;
的通项公式;
⑶求数列 的前
的前 项和
项和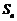 .
.
[解析]
⑴∵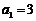 ,
,
 ,
,
∴ ,
, .
.
⑵证明:∵ ,
,
∴数列 是首项为
是首项为 ,公比为
,公比为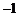 的等比数列.
的等比数列.
∴ ,即
,即 ,
,
∴ 的通项公式为
的通项公式为
 .
.
⑶∵ 的通项公式为
的通项公式为
 ,
,
所以,
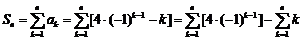

 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com