
22.解:(1)由点P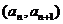 在直线
在直线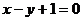 上,即
上,即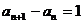 , …………2分
, …………2分
且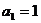 ,数列{
,数列{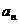 }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列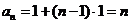 ,
,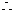
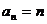 ……………4分
……………4分
(2)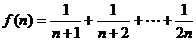
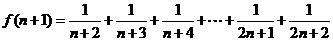 …………………6分
…………………6分
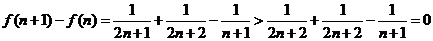
所以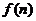 是单调递增,故
是单调递增,故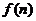 的最小值是
的最小值是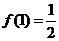 ……………10分
……………10分
(3)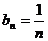 ,可得
,可得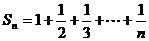 ,
,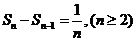 ……………11分
……………11分
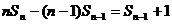 ……………12分
……………12分
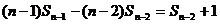
…………
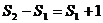
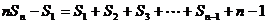
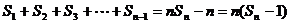 ,
,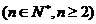 ……………14分
……………14分
13如果sin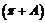 =
=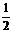 ,那么cos
,那么cos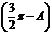 的值是
的值是
 14已知向量
14已知向量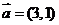 ,
,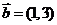 ,
,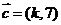 ,若
,若 ∥
∥ ,则
,则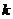 =
.
=
.
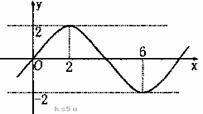
15函数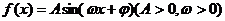 的图象如图所示,
的图象如图所示,
则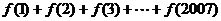 的值等于 .
的值等于 .
16若函数f(x)=a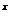 -x-a(a>0且a
-x-a(a>0且a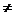 1)有两个零点,则实数a的取值范围是
1)有两个零点,则实数a的取值范围是
三解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算过程)
17(本小题满分12分)在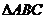 中,角
中,角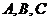 所对的边分别为
所对的边分别为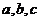 ,且满足
,且满足 , 向量数量积
, 向量数量积 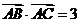 .
(1)求
.
(1)求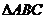 的面积;
(2)若
的面积;
(2)若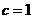 ,求
,求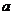 的值.
的值.
18(本小题满分12分)已知:向量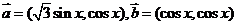 ,
,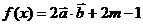 (
(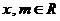 )
)
(1) 求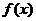 关于
关于 的表达式,并求
的表达式,并求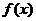 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2) 若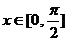 时,
时,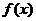 的最小值为5,求
的最小值为5,求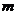 的值.
的值.
19(本小题满分12分)在等差数列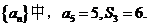
(1)

(2)
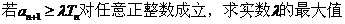 ;
;
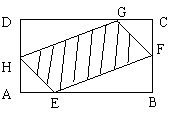 20 (本小题满分12分)如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地, 使其四个顶点分别落在矩形的四条边上,已知AB=
20 (本小题满分12分)如图,有一块矩形空地,要在这块空地上辟一个内接四边形为绿地, 使其四个顶点分别落在矩形的四条边上,已知AB=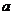 (
(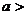 2),BC=2,且AE=AH=CF=CG,设AE=
2),BC=2,且AE=AH=CF=CG,设AE= ,绿地面积为
,绿地面积为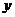 .
.
(1)写出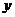 关于
关于 的函数关系式,并指出这个函数的定义域.
的函数关系式,并指出这个函数的定义域.
(2)当AE为何值时,绿地面积最大?
21(本小题满分12分)已知函数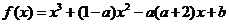
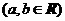 .
.
(1)若函数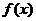 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是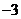 ,求
,求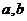 的值;
的值;
(2)若函数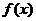 在区间
在区间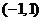 上不单调,求
上不单调,求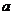 的取值范围.
的取值范围.
22(本小题满分14分)已知数列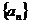 中,
中,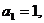 且点
且点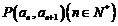 在直线
在直线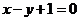 上.
上.
(1)求数列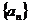 的通项公式;
的通项公式;
(2)若函数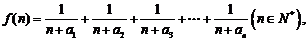 求函数
求函数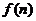 的最小值;
的最小值;
(3)设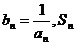 表示数列
表示数列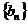 的前
的前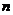 项和,
项和,
试证明: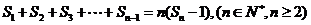 .
.
17解析:(Ⅰ)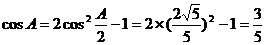
又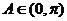 ,
,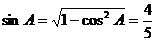 ,而
,而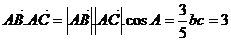 ,所以
,所以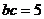 ,所以
,所以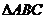 的面积为:
的面积为: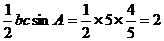
(Ⅱ)由(Ⅰ)知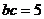 ,而
,而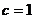 ,所以
,所以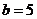
所以
18解:(Ⅰ) 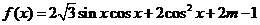 ……2分
……2分
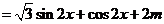 ……………………………………………………4分
……………………………………………………4分
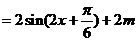 . …………………………………………………………6分
. …………………………………………………………6分
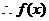 的最小正周期是
的最小正周期是 . …………………………………………………7分
. …………………………………………………7分
(Ⅱ) ∵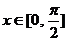 ,
,
∴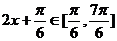 . ………………………………………………………9分
. ………………………………………………………9分
∴当 即
即 时,函数
时,函数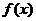 取得最小值是
取得最小值是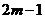 . ………11分
. ………11分
∵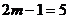 ,
,
∴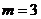 . ………………………………………………………………………13分
. ………………………………………………………………………13分
20.(Ⅰ)SΔAEH=SΔCFG=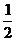 x2, ………………1分
x2, ………………1分
SΔBEF=SΔDGH=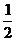 (a-x)(2-x)。 ………………2分
(a-x)(2-x)。 ………………2分
∴y=SABCD-2SΔAEH-2SΔBEF=2a-x2-(a-x)(2-x)=-2x2+(a+2)x。……5分
由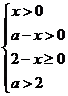 ,得
,得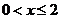 ………………6分
………………6分
∴y=-2x2+(a+2)x,0<x≤2 ………………7分
(Ⅱ)
当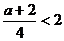 ,即a<6时,则x=
,即a<6时,则x=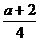 时,y取最大值
时,y取最大值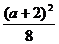 。…………9分
。…………9分
当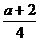 ≥2,即a≥6时,y=-2x2+(a+2)x,在
≥2,即a≥6时,y=-2x2+(a+2)x,在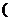 0,2]上是增函数,
0,2]上是增函数,
则x=2时,y取最大值2a-4 ………………12分
综上所述:当a<6时,AE=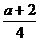 时,绿地面积取最大值
时,绿地面积取最大值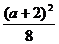 ;
;
当a≥6时,AE=2时,绿地面积取最大值2a-4 …………………14分
21解析:(Ⅰ)由题意得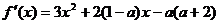
又 ,解得
,解得 ,
,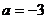 或
或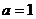
(Ⅱ)函数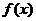 在区间
在区间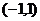 不单调,等价于
不单调,等价于
导函数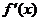 在
在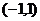 既能取到大于0的实数,又能取到小于0的实数
既能取到大于0的实数,又能取到小于0的实数
即函数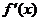 在
在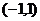 上存在零点,根据零点存在定理,有
上存在零点,根据零点存在定理,有
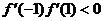 , 即:
, 即: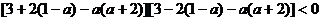
整理得: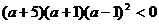 ,解得
,解得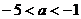
12.设a>0,f(x)=ax2+bx+c,曲线y=f(x)在点P(x0,f(x0))处切线的倾斜角的取值范围为[0,],则点P到曲线y=f(x)对称轴距离的取值范围为( )
A、[0,] B、[0,] C、[0,||] D、[0,||]
第Ⅱ卷(非选择题 共90分)
11.已知函数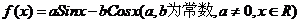 的图像关于直线
的图像关于直线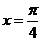 对称,则函数
对称,则函数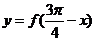 是( )
是( )
A、偶函数且它的图像关于点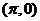 对称 B、偶函数且它的图像关于点
对称 B、偶函数且它的图像关于点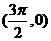 对称
对称
C、奇函数且它的图像关于点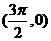 对称 D、奇函数且它的图像关于点
对称 D、奇函数且它的图像关于点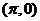 对称
对称
9. 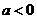 是方程
是方程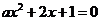 至少有一个负数根的( )
至少有一个负数根的( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
10函数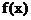 对任意正整数a、b满足条件
对任意正整数a、b满足条件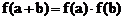 ,且
,且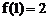 。则
。则 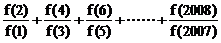 的值是( )
的值是( )
A. 2007 B. 2008 C. 2006 D. 2005
8.函数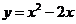 ,
, 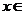 [0,3]的值域为(
)
[0,3]的值域为(
)
A. [0,3] B. [1,3] C. [-1,0] D.[-1,3]
7、设曲线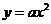 在点
在点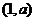 处的切线与直线
处的切线与直线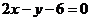 平行,则
平行,则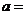 ( )
( )
A、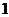 B、
B、 C、
C、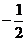 D、
D、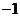
6.函数 若
若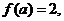 则
则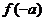 的值为( )
的值为( )
A、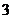 B、
B、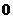 C、
C、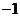 D、
D、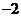
5.函数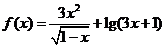 的定义域是( )
的定义域是( )
A、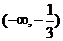 B、
B、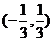 C、
C、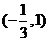 D、
D、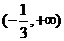
4.已知等比数列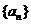 满足
满足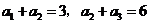 ,则
,则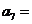 ( )
( )
A.64 B.81 C.128 D.243
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com