
2.设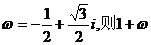 等于( ▲ )
等于( ▲ )
A. B.
B. C.
C.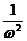 D.
D.
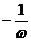
1.已知全集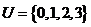 ,集合
,集合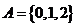 ,
, ,则
,则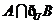 等于( ▲ )
等于( ▲ )
A.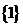 B.
B.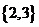 C.
C. 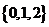 D.
D. 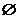
(18) 本题满分14分
(Ⅰ) 解: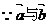 共线 ∴
共线 ∴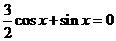
∴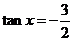 ………………………………………………………………………(5分)
………………………………………………………………………(5分)
(II)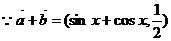
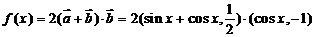
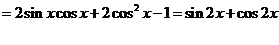
 ,令
,令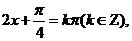 得
得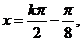
所以函数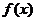 图像的对称中心的坐标是
图像的对称中心的坐标是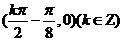
(写出其中的一个点)……………………………………………………………(14分)
(19) 本题满分14分
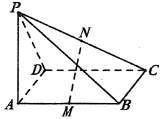 (I) 证明:如图,取PD的中点E,连结AE、EN
(I) 证明:如图,取PD的中点E,连结AE、EN
则有EN//CD// AM,
且EN=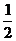 CD=
CD=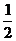 AB=MA.
AB=MA.
∴四边形AMNE是平行四边形.
∴MN//AE。
∵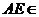 平面
平面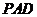 ,
,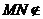 平面
平面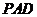 ,
,
∴MN//平面PAD。……………………………………………(6分)
(II)解:∵PA⊥平面ABCD,∴PA⊥AD.
又∠PDA=45°,E是PD中点,
∴∠EAD=45°又MN//AE
∴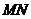 与平面
与平面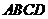 所成的角等于∠EAD,
所成的角等于∠EAD,
∴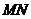 与平面
与平面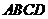 所成的角等于45°…………………(14分)
所成的角等于45°…………………(14分)
(20) 本题满分14分
(Ⅰ)证明: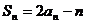 ,
, 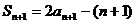
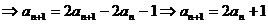 ,
,
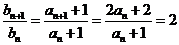 又由
又由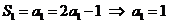
所以数列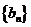 是首项为
是首项为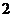 ,公比为
,公比为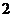 的等比数列…………………(7分)
的等比数列…………………(7分)
(Ⅱ)解: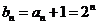 ,
,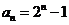
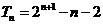 ,
,
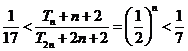
所以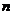 的值为3,4……………………………………………………(14分)
的值为3,4……………………………………………………(14分)
(21)本题满分15分
(Ⅰ) 解: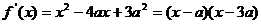 ,因为
,因为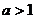 ,所以
,所以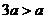 ,
,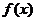 的极小值为
的极小值为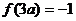 ……………………………………………(6分)
……………………………………………(6分)
(Ⅱ) 解: 若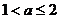 时,当
时,当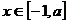 时
时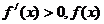 在
在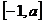 上递增,
上递增,
当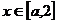 时
时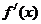 <
<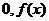 在
在 上递减,所以
上递减,所以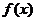 的最大值为
的最大值为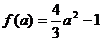 ,令
,令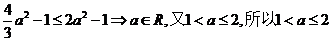 ;
;
若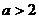 时,当
时,当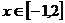 时
时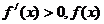 在
在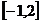 上递增,所以
上递增,所以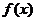 的最大值为
的最大值为
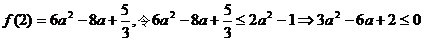
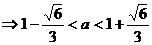 ,又
,又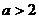 ,所以无解。
,所以无解。
由上可在知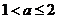 ……………………………………………(15分)
……………………………………………(15分)
(22) 本题满分15分
(Ⅰ)
解:(1) ,
,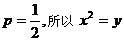 …………………………(5分)
…………………………(5分)
(Ⅱ) 解: B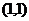 ,设
,设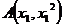 ,
,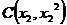 ,
,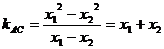
设BC的斜率为k,则
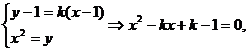
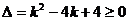 ,
,
又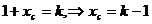 ,C
,C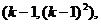 A
A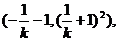
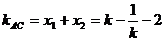 ,
,
直线AC的方程为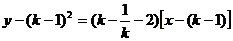 ,
,
令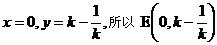
AD: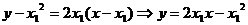
同理CD: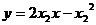 ,联立两方程得D
,联立两方程得D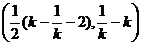
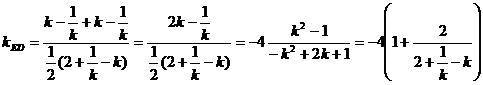
令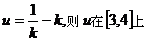 递减,所以,当
递减,所以,当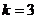 时,
时,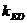 最大为8
最大为8
所以,BC的方程为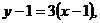 即
即 ……………………………(15分)
……………………………(15分)
(11) 4 (12)
5
(13) 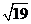 (14)
(14)
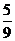
(15) 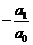 (16)
(16)
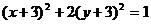 (17)
(17)
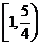
(1) A (2) B (3) B (4) C (5) D
(6) C (7) C (8) D (9) A (10) C
22.(本小题满分15分)
已知圆 过点
过点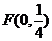 , 且与直线
, 且与直线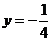 相切.
相切.
(Ⅰ)求圆心 的轨迹
的轨迹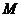 的方程;
的方程;
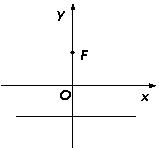 (Ⅱ)若直角三角形
(Ⅱ)若直角三角形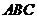 的三个顶点在轨迹
的三个顶点在轨迹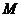 上,且点
上,且点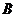 的横坐标为1,过点
的横坐标为1,过点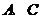 分别作轨迹
分别作轨迹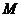 的切线,两切线相交于点
的切线,两切线相交于点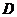 ,直线
,直线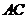 与
与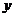 轴交于点
轴交于点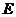 ,当直线
,当直线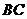 的斜率在
的斜率在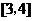 上变化时,直线
上变化时,直线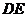 斜率是否存在最大值,若存在,求其最大值和直线
斜率是否存在最大值,若存在,求其最大值和直线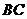 的方程;若不存在,请说明理由?
的方程;若不存在,请说明理由?
衢州市2010年4月高三年级教学质量检测答案
数学(文科)
21.(本小题满分15分)
已知函数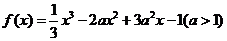 .
.
(Ⅰ)求函数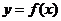 的极小值;
的极小值;
(Ⅱ)若对任意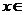
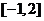 , 恒有
, 恒有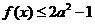 ,求
,求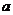 的取值范围.
的取值范围.
20.(本小题满分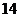 分)
分)
已知数列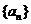 的前
的前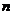 项和为
项和为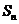 ,且对任意
,且对任意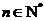 ,有
,有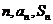 成等差数列.
成等差数列.
(Ⅰ)记数列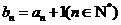 ,求证:数列
,求证:数列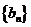 是等比数列.
是等比数列.
(Ⅱ)数列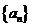 的前
的前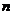 项和为
项和为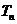 ,求满足
,求满足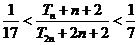 的所有
的所有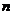 的值.
的值.
19.(本小题满分14分)
如图,PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点.
(I)求证:MN//平面PAD;
(II)若∠PDA=45°,求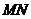 与平面
与平面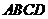 所成角的大小.
所成角的大小.

18.(本小题满分14分)已知向量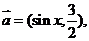
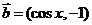
(I)当向量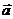 与向量
与向量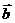 共线时,求
共线时,求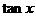 的值;
的值;
(II)求函数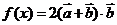 图像的一个对称中心的坐标.
图像的一个对称中心的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com