
5. 设函数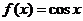 ,把
,把 的图象向右平移
的图象向右平移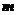 个单位后,图象恰好为函数
个单位后,图象恰好为函数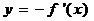 的图象,则
的图象,则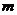 的值可以为 ▲
.
的值可以为 ▲
.
4. 已知点 、
、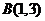 ,向量
,向量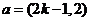 ,若
,若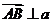 ,
,
则实数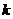 的值为 ▲
.
的值为 ▲
.
数学试卷 第1页(共4页)
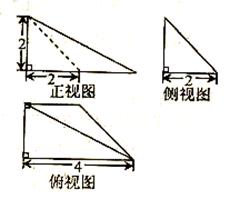
3. 已知一个空间几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 ▲
 。
。
2.
 复数
复数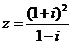 的共轭复数是 ▲ .
的共轭复数是 ▲ .
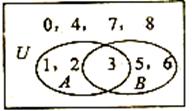
1. 已知全集U和集合A,B如图所示,则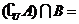 ▲
.
▲
.
19.(本题满分16分)
解析:(Ⅰ)因为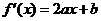 ,由图可知,
,由图可知,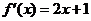 ,--------------------------2分
,--------------------------2分
∴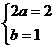 ,得
,得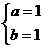 ,故所求函数解析式为
,故所求函数解析式为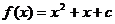 .---------------------4分
.---------------------4分
(Ⅱ)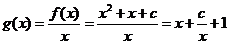 ,则
,则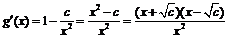 .--6分
.--6分
法一:①若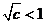 ,即
,即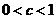 时,
时,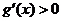 ,
,
∴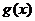 在
在 上是增函数,故
上是增函数,故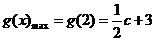 .---------------------------8分
.---------------------------8分
②若 ,即
,即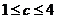 ,当
,当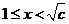 时,
时,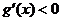 ;当
;当 时,
时,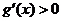 ;
;
∵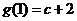 ,
,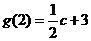 ,
,
∴当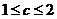 时,
时,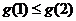 ,
,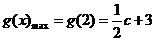 ;
;
当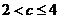 时,
时,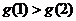 ,
,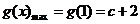 .-------------------------------12分
.-------------------------------12分
③若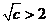 ,即
,即 时,
时,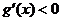 ,
,
∴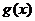 在
在 上是减函数,故
上是减函数,故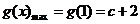 .-------------------------------14分
.-------------------------------14分
综上所述,当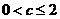 时,
时,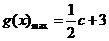 ;当
;当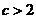 时,
时,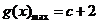 . ------16分
. ------16分
法二: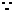 当
当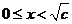 时,
时,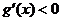 ;当
;当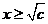 时,
时,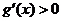 ;
----------8分
;
----------8分
∴当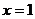 或
或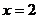 时,
时,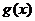 取得最大值,
取得最大值,
其中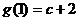 ,
,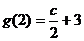 ,
,
当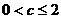 时,
时,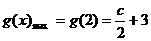 ;当
;当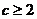 时,
时,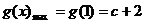 . ------16分
. ------16分
20解:(Ⅰ)由题意得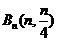 ,
,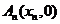 ,
,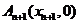 ,
,
∵点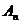 、
、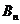 、
、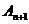 构成以
构成以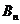 为顶点的等腰三角形,
为顶点的等腰三角形,
∴ ,即
,即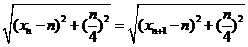
得
又∵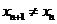 ,∴
,∴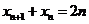 , ①
, ①
则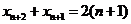 ②
②
由②-①得,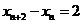 ,即
,即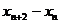 是常数.
-------------------------------6分
是常数.
-------------------------------6分
即所列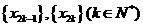 都是等差数列.
都是等差数列.
(注:可以直接由图像得到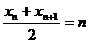 ,即
,即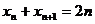 , (
, (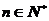 ) )
) )
当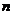 为正奇数时,
为正奇数时,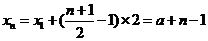 ,
,
当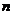 为正偶数时,由
为正偶数时,由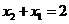 得,
得,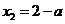 ,故
,故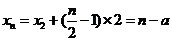 ,
,
∴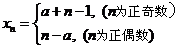 .
------------------------------8分
.
------------------------------8分
(Ⅱ)假设存在等腰直角三角形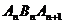 ,由题意
,由题意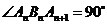 .
.
在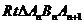 中,
中,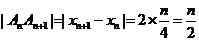 .
------------------------------10分
.
------------------------------10分
当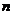 为正奇数时,
为正奇数时,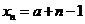 ,
,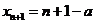 ,
,
∴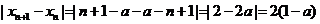 ,故有
,故有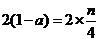 ,即
,即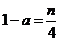 ,
,
又∵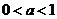 ,∴
,∴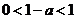 ,∴
,∴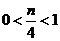 ,即
,即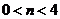 ,
,
∴当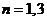 时,使得三角形
时,使得三角形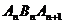 为等腰直角三角形.------------------------------12分
为等腰直角三角形.------------------------------12分
当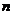 为正偶数时,
为正偶数时,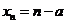 ,
,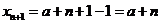 ,
,
∴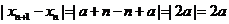 ,故有
,故有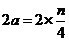 ,即
,即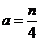 ,
,
又∵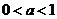 ,∴
,∴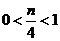 ,即
,即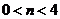 ,
,
∴当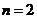 时,使得三角形
时,使得三角形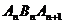 为等腰直角三角形.
------------------------------14分
为等腰直角三角形.
------------------------------14分
综上所述,当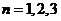 时,使得三角形
时,使得三角形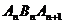 为等腰直角三角形. ------------------------------16分
为等腰直角三角形. ------------------------------16分
注:也可以回答为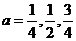 时,使得三角形
时,使得三角形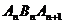 为等腰直角三角形.
为等腰直角三角形.
18. 解析:(Ⅰ)由 可得,
可得, . --------------------------------1分
. --------------------------------1分
∵直线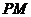 与曲线
与曲线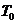 相切,且过点
相切,且过点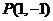 ,∴
,∴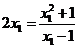 ,即
,即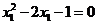 ,
,
∴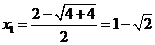 ,或
,或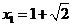 ,
-------------------------------3分
,
-------------------------------3分
同理可得: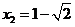 ,或
,或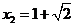 --------------------------------4分
--------------------------------4分
∵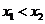 ,∴
,∴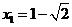 ,
,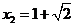 .
--------------------------------5分
.
--------------------------------5分
(Ⅱ)由(Ⅰ)知,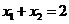 ,
,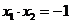 ,则直线
,则直线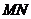 的斜率
的斜率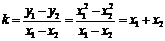 ,--∴直线
,--∴直线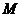 的方程为:
的方程为: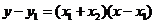 ,又
,又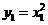 ,
,
∴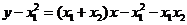 ,即
,即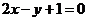 .--------------------------------7分
.--------------------------------7分
∵点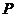 到直线
到直线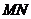 的距离即为圆
的距离即为圆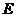 的半径,即
的半径,即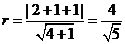 ,
--------------------8分
,
--------------------8分
故圆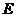 的面积为
的面积为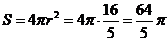 .
--------------------------------9分
.
--------------------------------9分
(Ⅲ)四边形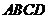 的面积为
的面积为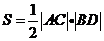
不妨设圆心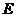 到直线
到直线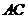 的距离为
的距离为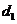 ,垂足为
,垂足为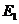 ;圆心
;圆心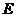 到直线
到直线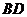 的距离为
的距离为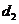 ,垂足为
,垂足为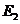 ;
;
则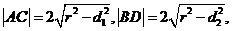 --------------------10分
--------------------10分
由于四边形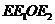 为矩形.且
为矩形.且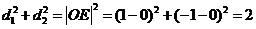 ------------13分
------------13分
所以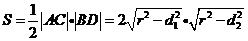
由基本不等式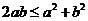 可得
可得
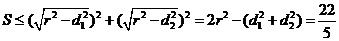 ,当且仅当
,当且仅当 时等号成立. ----------15分
时等号成立. ----------15分
注:(Ⅲ)解法较多,阅卷时可酌情给分.
17.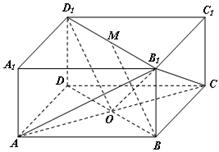 (本题满分15分)解析:(Ⅰ)连接
(本题满分15分)解析:(Ⅰ)连接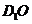 ,如图,
,如图,
∵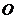 、
、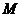 分别是
分别是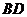 、
、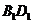 的中点,
的中点,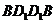 是矩形,
是矩形,
∴四边形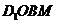 是平行四边形,
是平行四边形,
∴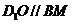 .--------2分
.--------2分
∵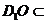 平面
平面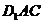 ,
,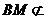 平面
平面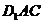 ,∴
,∴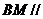 平面
平面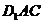 .------------------------4分
.------------------------4分
(Ⅱ)连接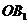 ,∵正方形
,∵正方形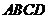 的边长为2,
的边长为2,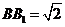 ,∴
,∴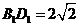 ,
,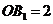 ,
,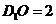 ,
,
则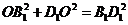 ,∴
,∴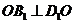 .
--------------------------------6分
.
--------------------------------6分
又∵在长方体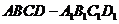 中,
中,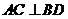 ,
,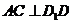 ,且
,且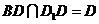 ,
,
∴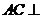 平面
平面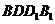 ,又
,又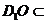 平面
平面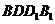 ,
,
∴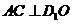 ,又
,又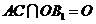 ,
-------------------------------10分
,
-------------------------------10分
∴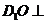 平面
平面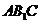 ,即
,即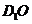 为三棱锥
为三棱锥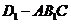 的高.--------------------------------12分
的高.--------------------------------12分
∵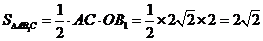 ,
,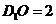
∴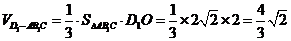 .--------------------------------145分
.--------------------------------145分
16. (本题满分14分)
(本题满分14分)
解析:(Ⅰ)分数在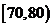 内的频率为:
内的频率为:
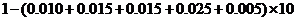
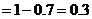 ,故
,故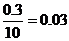 ,
,
如图所示: -----------------------6分
(求频率2分,作图2分)
(Ⅱ)平均分为:
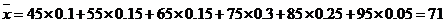 .----------------7分
.----------------7分
(Ⅲ)由题意,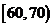 分数段的人数为:
分数段的人数为: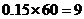 人; ----------------8分
人; ----------------8分
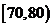 分数段的人数为:
分数段的人数为: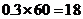 人; ----------------9分
人; ----------------9分
∵在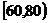 的学生中抽取一个容量为
的学生中抽取一个容量为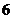 的样本,
的样本,
∴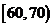 分数段抽取2人,分别记为
分数段抽取2人,分别记为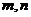 ;
;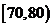 分数段抽取4人,分别记为
分数段抽取4人,分别记为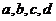 ;
;
设从样本中任取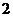 人,至多有1人在分数段
人,至多有1人在分数段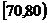 为事件
为事件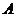 ,则基本事件空间包含的基本事件有:
,则基本事件空间包含的基本事件有:
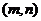 、
、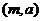 、
、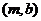 、
、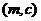 、
、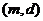 、……、
、……、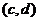 共15种,
共15种,
则事件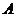 包含的基本事件有:
包含的基本事件有:
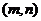 、
、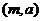 、
、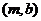 、
、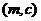 、
、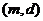 、
、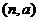 、
、 、
、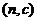 、
、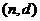 共9种,----12分
共9种,----12分
∴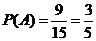 . --------------------------------14分
. --------------------------------14分
5.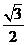 6.
6. 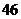 7.22 8.
7.22 8.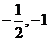 9.
9. 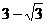 10.
10. 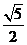 11.
11.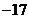 12. (4) 13
12. (4) 13 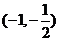 14.
14. 
15解析:(Ⅰ)∵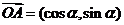 ,∴
,∴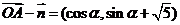 , ……………1分
, ……………1分
∵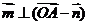 ,∴
,∴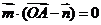 ,即
,即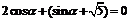 ① ………2分
① ………2分
又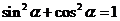 ②
②
由①②联立方程解得,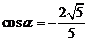 ,
,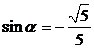 .
………………5分
.
………………5分
∴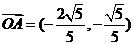 ……………………………………6分
……………………………………6分
(Ⅱ)∵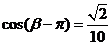 即
即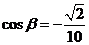 ,
,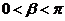 ,
…………7分
,
…………7分
∴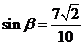 ,
,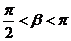 ……………8分
……………8分
又∵ ,
………………10分
,
………………10分
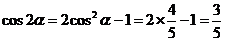 ,
………………………12分
,
………………………12分
∴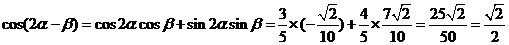 .14分
.14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com