
1.人体中内环境稳态所包含的内容不包括 
A.线粒体基质中pH的相对稳定
B.血浆中各种化学成分的相对稳定 
C.组织液温度的相对稳定
D.血浆渗透压的相对稳定 
20. 解:(1)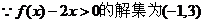 ,∴可设
,∴可设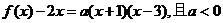 ,
,
因而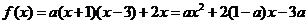 ①
①

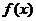 =
=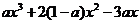 ,
,
∵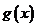 在区间
在区间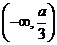 内单调递减,
内单调递减,
∴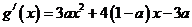 在
在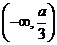 上的函数值非正,
上的函数值非正,
由于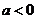 ,对称轴
,对称轴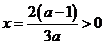 ,故只需
,故只需 ,注意到
,注意到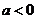 ,∴
,∴ ,得
,得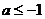 或
或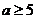 (舍去).
(舍去).
故所求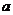 的取值范围是
的取值范围是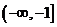 .
.
(2) 时,方程
时,方程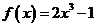 仅有一个实数根,即证方程
仅有一个实数根,即证方程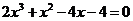 仅有一个实数根.令
仅有一个实数根.令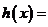
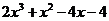 ,由
,由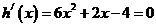 ,得
,得 ,
,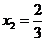 ,易知
,易知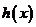 在
在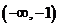 ,
,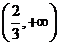 上递增,在
上递增,在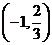 上递减,
上递减,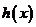 的极大值
的极大值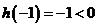 ,故函数
,故函数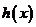 的图像与
的图像与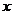 轴仅有一个交点,∴
轴仅有一个交点,∴ 时,方程
时,方程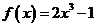 仅有一个实数根,得证.
仅有一个实数根,得证.
(3)设 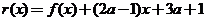 =
= 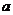 x2+x+1,
x2+x+1,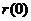 =1,对称轴为
=1,对称轴为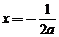 ,.
,.
由题意,得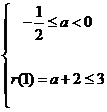 或
或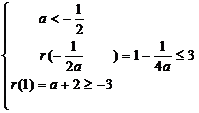
解出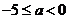 ,故使|
,故使|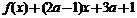 |≤3成立的充要条件是
|≤3成立的充要条件是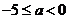
19.本题主要考查将实际问题转化为数学问题的能力,以及综合运用函数知识解决问题的能力.
解
设供应站坐标为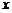 ,各工作台上的所有工人到供应站的距离之和为
,各工作台上的所有工人到供应站的距离之和为 .
.
(Ⅰ)由题设知,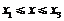 ,所以
,所以
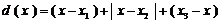
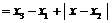 . ……6分
. ……6分
故当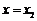 时,
时, 取最小值,此时供应站的位置为
取最小值,此时供应站的位置为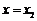 . ……8分
. ……8分
(Ⅱ)由题设知,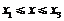 ,所以各工作台上的所有工人到供应站的距离之和为
,所以各工作台上的所有工人到供应站的距离之和为
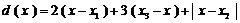 . ……12分
. ……12分
且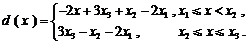 ……14分
……14分
因此,函数 在区间
在区间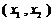 上是减函数,在区间
上是减函数,在区间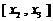 上是常数.故供应站位置位于区间
上是常数.故供应站位置位于区间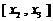 上任意一点时,均能使函数
上任意一点时,均能使函数 取得最小值,且最小值为
取得最小值,且最小值为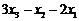 ,
,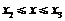 . ……16分
. ……16分
18. 本题主要考查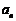 与
与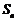 的关系,等差数列,等比数列等基础知识,同时考查分析问题和解决问题的能力.满分15分.
的关系,等差数列,等比数列等基础知识,同时考查分析问题和解决问题的能力.满分15分.
解 (Ⅰ)令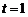 ,
,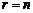 ,得
,得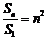 ,于是
,于是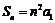 . ……
. ……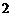 分
分
当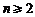 时,
时,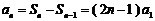 ;
;
当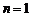 时,
时,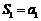 也适合上式.
也适合上式.
综上知,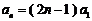 . ……
. ……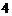 分
分
所以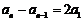 .
.
故数列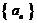 是公差
是公差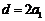 的等差数列. ……8分
的等差数列. ……8分
(Ⅱ)当 时,由(Ⅰ)知,
时,由(Ⅰ)知,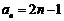 .
.
于是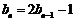 ,即
,即 .
.
因此数列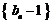 是首项为
是首项为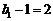 ,公比为
,公比为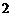 的等比数列,所以
的等比数列,所以
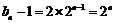 .即
.即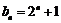 . ……12分
. ……12分
故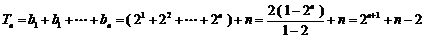 .……15分
.……15分
17.本题主要考查直线,椭圆,函数,导数以及向量等基础知识,同时考查综合运用数学知识解决问题的能力.
解 (Ⅰ)设点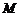 的坐标为
的坐标为 ,由图可知
,由图可知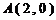 ,
,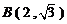 ,
,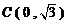 ,
,
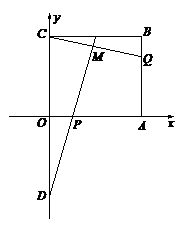
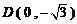 .
.
由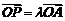 ,得点
,得点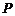 的坐标为
的坐标为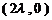 ;
;
由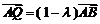 ,得点
,得点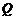 的坐标为
的坐标为
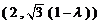 .
……
.
……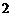 分
分
于是,当 时,直线
时,直线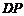 的方程为
的方程为
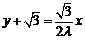 ,
……①
,
……①
直线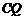 的方程为
的方程为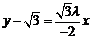 . ……②
. ……②
①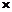 ②,得
②,得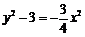 ,即
,即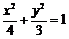 .
.
当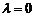 时,点
时,点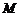 即为点
即为点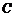 ,而点
,而点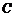 的坐标
的坐标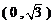 也满足上式.
也满足上式.
故点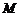 的轨迹方程为
的轨迹方程为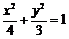 . ……
. …… 分
分
(Ⅱ)设过点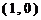 的直线
的直线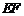 的方程为
的方程为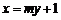 ,且设
,且设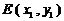 ,
,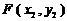 .
.
由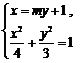 得
得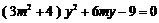 . ……③
. ……③
由于上述方程的判别式 ,所以
,所以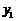 ,
,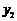 是方程③的两根,
是方程③的两根,
根据求根公式,可得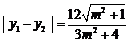 .
.
又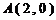 ,所以
,所以 的面积
的面积 . ……
. …… 分
分
令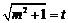
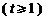 ,则
,则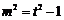 .
.
于是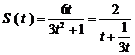 ,
,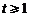 .
.
记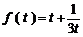 ,
,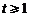 ,则
,则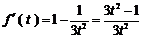 .
.
因为当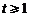 时,
时,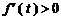 ,所以
,所以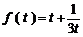 在
在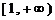 上单调递增.
上单调递增.
故当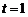 时,
时,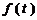 取得最小值
取得最小值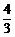 ,此时
,此时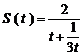 取得最大值
取得最大值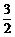 .
.
综上所述,当 时,即直线
时,即直线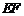 垂直于
垂直于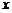 轴时,
轴时, 的面积取得最大值
的面积取得最大值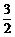 .
.
……15分
16. 本题主要考查线线,线面关系的基础知识,同时考查空间想象能力和推理运算能力.
解 (Ⅰ)因为 ,
,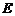 分别是
分别是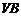 ,
,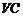 的中点,所以
的中点,所以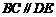 ,因此
,因此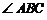 是异面直线
是异面直线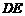
与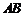 所成的角. ……
所成的角. ……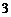 分
分
又因为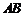 是圆
是圆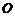 的的直径,点
的的直径,点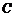 是弧
是弧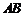 的
的
中点,所以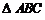 是以
是以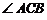 为直角的等腰直角三角形.于是
为直角的等腰直角三角形.于是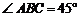 .
.
故异面直线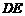 与
与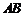 所成的角为
所成的角为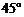 .……7分
.……7分
(Ⅱ)因为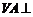 平面
平面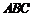 ,
,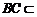 平面
平面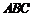 ,所以
,所以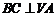 . ……10分
. ……10分
由(Ⅰ)知,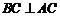 ,所以
,所以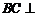 平面
平面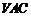 .
……12分
.
……12分
又由(Ⅰ)知,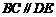 ,故
,故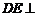 平面
平面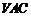 .
……14分
.
……14分
15.本题主要考查向量、三角函数的基础知识,同时考查根据相关公式合理变形正确运算的能力.
解 (Ⅰ) 由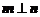 ,得
,得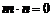 ,即
,即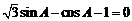 . ……
. ……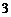 分
分
所以 ,即
,即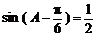 .
.
因为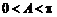 ,所以
,所以 . ……7分
. ……7分
(Ⅱ)由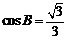 ,得
,得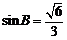 . ……10分
. ……10分
依正弦定理,得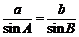 ,即
,即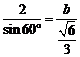 . ……13分
. ……13分
解得,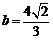 . ……14分
. ……14分
12. 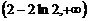 13.
13. 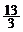 14.(1)
14.(1)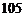 ; (2)
; (2)
7.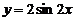 的图象向右平移
的图象向右平移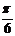 个单位长度 8.
个单位长度 8.  9.
9. 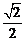 10.
10.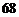 11. 2550
11. 2550
1.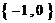 2.
2.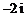 3.
3.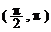 4.
4.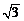 5.
5. 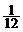 6.
6.  安
安
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com