
下图为“厄尔尼诺发生时太平洋表层水温异常现象示意图”。 图中等值线为太平洋海域表面水温正距平(℃)。读图回答2-3题。
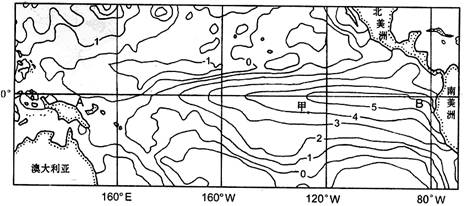
2.据图判断,太平洋海域表面水温正距平“≥5℃”的海区在赤道上延伸约
A.3500km B.6500km C.5000km D.4000km
3.下列关于赤道附近A、B两地的叙述正确的是
A.A地降水增加,气候更加湿润
B.A地上升气流较正常年份减弱
C.B地气温升高,气候干燥少雨
D.B地下沉气流较正常年份增强
1.不同的民居特点反映了所在地区的地理环境特点。下面四地民居特点与其所在地区环境及人类活动搭配正确的是

A.①--气温低,冬季酷寒、烈风--冰雪穴居,抗风御寒
B.②--终年干旱少雨--半穴居,防热、防寒、防风沙
C.③--终年湿热--傍水而居,交通便利
D.④--夏季炎热潮湿--圆形石屋,防暑防潮
21.(本题满分14分)
已知数列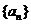 和
和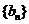 满足
满足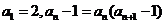 ,
, ,数列
,数列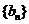 的前
的前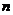 和为
和为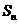 .
.
(1)求数列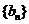 的通项公式;
的通项公式;
 (2)设
(2)设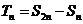 ,求证:
,求证: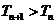 ;
;
(3)求证:对任意的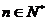 有
有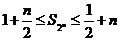 成立.
成立.
20.(本题满分14分)
设函数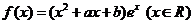 .
.
(1)若 是函数
是函数 的一个极值点,试求出
的一个极值点,试求出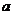 关于
关于 的关系式(用
的关系式(用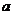 表示
表示 ),并确定
),并确定 的单调区间;
的单调区间;
(2)在(1)的条件下,设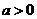 ,函数
,函数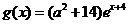 .若存在
.若存在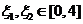 使得
使得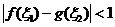 成立,求
成立,求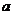 的取值范围.
的取值范围.
19. (本题满分14分)
(本题满分14分)
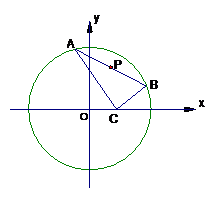
已知点C(1,0),点A、B是⊙O: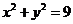 上任意两个不同的点,
上任意两个不同的点,
且满足 ,设P为弦AB的中点.
,设P为弦AB的中点.
(1)求点P的轨迹T的方程;
(2)试探究在轨迹T上是否存在这样的点:它到直线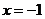 的
的
距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,
说明理由.
18. (本题满分14分)
(本题满分14分)
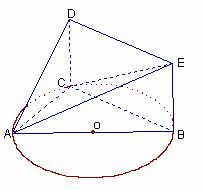
如图,△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行
四边形,DC 平面ABC ,
平面ABC , ,已知AE与平面ABC所成的角为
,已知AE与平面ABC所成的角为 ,
,
 且
且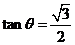 .
.
(1)证明:平面ACD 平面
平面 ;
;
(2)记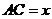 ,
,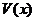 表示三棱锥A-CBE的体积,求
表示三棱锥A-CBE的体积,求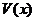 的表达式;
的表达式;
(3)当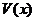 取得最大值时,求二面角D-AB-C的大小.
取得最大值时,求二面角D-AB-C的大小.
17. (本题满分12分)
某射击运动员为争取获得2010年广州亚运会的参赛资格正在加紧训练.已知在某次训练中他射击了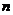 枪,每一枪的射击结果相互独立,每枪成绩不低于10环的概率为
枪,每一枪的射击结果相互独立,每枪成绩不低于10环的概率为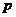 ,设
,设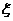 为本次训练中成绩不低于10环的射击次数,
为本次训练中成绩不低于10环的射击次数,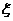 的数学期望
的数学期望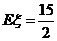 ,方差
,方差 .
.
(1)求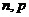 的值;
的值;
(2)训练中教练要求:若有5枪或5枪以上成绩低于10环,则需要补射,求该运动员在本次训练中需要补射的概率.
(结果用分数表示.已知: ,
,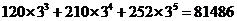 )
)
16.(本题满分12分)
设向量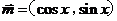 ,
,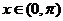 ,
,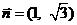 .
.
(1)若 ,求
,求 的值;
的值;
(2)设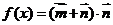 ,求函数
,求函数 的值域.
的值域.
(二)选做题(14、15题,考生只能从中选做一题 )
)
14.(几何证明选做题)如图,在 中,
中,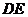 //
//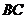 ,
,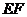 //
//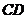 ,若
,若
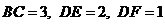 ,则AB的长为___________.
,则AB的长为___________.
15.(坐标系与参数方程选做题)
如果曲线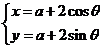 (
( 为参数)上有且仅有两个点到原点的距
为参数)上有且仅有两个点到原点的距
离为2,则实数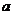 的取值范围是_________.
的取值范围是_________.
(一)必做题(9-13题)
9.已知向量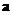 、
、 的夹角为120°,且
的夹角为120°,且 ,则
,则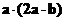 的值为
.
的值为
.
10.在同一平面直角坐标系中,已知函数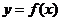 的图象与
的图象与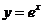 的图象关于直线
的图象关于直线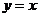 对称,则函数
对称,则函数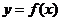 对应的曲线在点(
对应的曲线在点(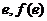 )处的切线方程为
.
)处的切线方程为
.
11.设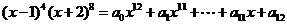 ,则
,则 = .
= .
12.有下列各式: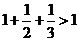 ,
, ,
,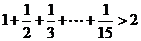 ,……
,……
则按此规律可猜想此类不等式的一般形式为: .
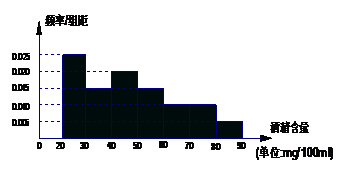
13.2009年8月15日晚8时开始某市交警一队在该市一交通岗前设点对过往的车辆进行抽查,经过两个小时共查出酒后驾车者60名,图甲是对这60名酒后驾车者血液中酒精浓度进行检测后依所得结果画出的频率分布直方图,则其中酒精浓度在70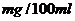 (含70)以上人数约为 ,统计方法中,同一组数据常用该组区间的中点值作为代表,图乙的程序框图是对这60名酒后驾车者血液的酒精含量做进一步的统计,则图乙输出的S值为
.(图甲中每组包括左端点,不包括右端点,图乙中数据
(含70)以上人数约为 ,统计方法中,同一组数据常用该组区间的中点值作为代表,图乙的程序框图是对这60名酒后驾车者血液的酒精含量做进一步的统计,则图乙输出的S值为
.(图甲中每组包括左端点,不包括右端点,图乙中数据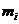 与
与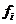 分别表示图甲中各组的组中值及频率)
分别表示图甲中各组的组中值及频率)


图甲 图乙
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com