
21. (本题满分12分)如图
(本题满分12分)如图 是某圆周四等分点中的一个,圆周上的动点
是某圆周四等分点中的一个,圆周上的动点 在四个分点上按逆时针方向运动,现投掷一个质地均匀的正四面体(四个面上分别写有1,2,3,4四个数字),投掷后底面上的数字为
在四个分点上按逆时针方向运动,现投掷一个质地均匀的正四面体(四个面上分别写有1,2,3,4四个数字),投掷后底面上的数字为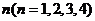 ,若
,若 从
从 出发,每投掷一次正四面体,点
出发,每投掷一次正四面体,点 就前进
就前进 个分点,且
个分点,且 点运动一周前连续投掷这个四面体.
点运动一周前连续投掷这个四面体.
(说明:正四面体就是空间四边形的边长和对角线都相等的几何体)
(Ⅰ)求投掷两次,点 恰好返回
恰好返回 点的概率;
点的概率;
(Ⅱ) 求 点恰好返回
点恰好返回 点的概率。
点的概率。
22已知椭圆 的离心率为
的离心率为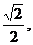 其左、右焦点分别为
其左、右焦点分别为 ,点P是坐标平面内一点,且
,点P是坐标平面内一点,且 (O为坐标原点)。
(O为坐标原点)。
(1)求椭圆C的方程;
(2)过点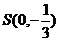 且斜率为k的动直线
且斜率为k的动直线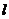 交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出M的坐标和
交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出M的坐标和 面积的最大值;若不存在,说明理由。
面积的最大值;若不存在,说明理由。
19. (本小题满分12分) 已知圆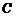 方程为:
方程为: .
.
(1)直线 过点
过点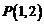 ,且与圆
,且与圆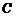 交于
交于 、
、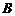 两点,若
两点,若 ,求直线
,求直线 的方程;
的方程;
(2)过圆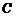 上一动点
上一动点 作平行于
作平行于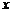 轴的直线
轴的直线 ,设
,设 与
与 轴的交点为
轴的交点为 ,若向量
,若向量 ,求动点
,求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
19.(12分)长方体ABCD-EFGH中,K为边BC的中点,M、N分别为HC、AK的中点,设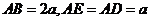 .
.
(1)求证:MN∥平面ADHE;(2)求异面直线HC和AK所成的角.

18.(本题满分12分)某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中的2次测试即可获得足够学分升上大学继续学习,不用参加后面的测试,而每个学生最多也只能参加5次测试,假设某学生每次通过测试的概率都是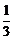 ,每次测试通过与否相互独立.规定:若前4次都没有通过测试,则第5次不能参加测试.
,每次测试通过与否相互独立.规定:若前4次都没有通过测试,则第5次不能参加测试.
(Ⅰ)求该学生恰好经过4次测试考上大学的概率;(Ⅱ)求该学生考上大学的概率.
17. 用数字0,1,2,3,4,5组成没有重复数字的四位数.
(1)可以组成多少个不同的四位数? (2)可以组成多少个不同的四位偶数?
(3)可以组成多少个能被3整除的四位数?
16.  如图,已知椭圆
如图,已知椭圆 的左、右准线分别为
的左、右准线分别为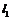 、
、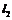 ,且分别交
,且分别交 轴于
轴于 、
、 两点,从
两点,从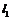 上一点
上一点 发出一条光线经过椭圆的左焦点
发出一条光线经过椭圆的左焦点 被
被 轴反射后与
轴反射后与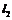 交于点
交于点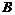 ,若
,若 ,且
,且 ,则椭圆的离心率等于
,则椭圆的离心率等于
15.设 ,
,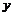 满足约束条件
满足约束条件 若目标函数
若目标函数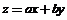 (
( ,
, )的最大
)的最大
值为12,则 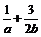 的最小值为
.
的最小值为
.
14.从1,2,3,4,5,6,7,8,9,10这10个号码中任意抽取3个号码,则所抽取的3个号码中,仅有两个号码是连续整数的概率为_________
13.在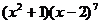 的展开式中x3的系数是
的展开式中x3的系数是
12.在正方体上任取三个顶带你连成三角形,则所得的三角形是等腰三角形的概率是( )
A. B.
B.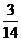 C.
C.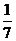 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com