
2. 官能团的消除
⑴通过加成反应可以消除C=C或C≡C。如CH2=CH2 +
H2 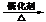 CH3CH3
CH3CH3
⑵通过消去、氧化可消除-OH。如CH3CH2OH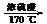 CH2=CH2↑ +
H2O
CH2=CH2↑ +
H2O
2CH3CH2OH + O2 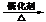 2CH3CHO + 2H2O
2CH3CHO + 2H2O
⑶通过加成或氧化可消除-CHO。如2CH3CHO
+ O2 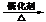 2CH3COOH
2CH3COOH
CH3CHO + H2 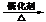 CH3CH2OH
CH3CH2OH
⑷通过水解反应消除-COO-。如CH3COOC2H5 + H2O → CH3COOH + C2H5OH
1. 官能团的引入
⑴引入C─C:C═C或C≡C与H2加成;
⑵引入C═C或C≡C:卤代烃或醇的消去;
⑶苯环上引入
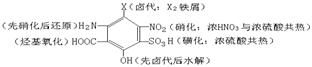
⑷引入─X:①在饱和碳原子上与X2(光照)取代;②不饱和碳原子上与X2或HX加成;③醇羟基与HX取代。
⑸引入─OH:①卤代烃水解;②醛或酮加氢还原;③C═C与H2O加成。
⑹引入─CHO或酮:①醇的催化氧化;②C≡C与H2O加成。
⑺引入─COOH:①醛基氧化;②─CN水化;③羧酸酯水解。
⑻引入─COOR:①醇酯由醇与羧酸酯化;②酚酯由酚与羧酸酐取代。
⑼引入高分子:①含C═C的单体加聚;②酚与醛缩聚、二元羧酸与二元醇(或羟基酸)酯化缩聚、二元羧酸与二元胺(或氨基酸)酰胺化缩聚。
2.同分异构体数目的判断方法
⑴记忆法。记住已掌握的常见的异构体数。例如:
①凡只含一个碳原子的分子均无异构体;甲烷、乙烷、新戊烷(看作CH4的四甲基取代物)、2,2,3,3-四甲基丁烷(看作乙烷的六甲基取代物)、苯、环己烷、C2H2、C2H4等分子的一卤代物只有一种。
②丙基、丁烷有两种;戊烷、二甲苯有三种。
⑵基元法。例如:丁基(C4H9-)有4种,则丁醇(C4H9-OH)、一氯丁烷(C4H9-Cl)或C4H10的一氯代物、戊醛(C4H9-CHO)、戊酸(C4H9-COOH)等都有4种(均指同类有机物)。
⑶替代法。例如:二氯苯C6H4Cl2有3种,四氯苯也有3种;又如CH4一卤代物只有一种,新戊烷C(CH3)4的一卤代物也只有一种。
⑷等效氢原子法。判断有机物发生取代反应后,能形成几种同分异构体的规律,可通过分析有几种等效氢原子法(又称对称法)来得出结论。
①同一碳原子上的氢原子是等效的。
②同一碳原子上所连甲基上的氢原子是等效的。
③处于镜面对称位置上的氢原子是等效的(相当于平面镜成像时,物与像的关系)
1.常见的类别异构
|
组成通式 |
可能的类别 |
典型实例 |
|
CnH2n |
烯烃、环烷烃 |
CH2==CH-CH3与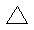 |
|
CnH2n -2 |
炔烃、二烯烃等 |
CH≡C-CH2CH3与 CH2==CHCH==CH2 |
|
CnH2n +2O |
醇、醚 |
C2H5OH与CH3OCH3 |
|
CnH2n O |
醛、酮、烯醇、环醚、环醇等 |
CH3CH2CHO、CH3COCH3、CH2==CHCH2OH、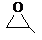 |
|
CnH2n O2 |
羧酸、酯 |
CH3COOH与HCOOCH3 |
|
CnH2n -6O |
酚、芳香醇、芳香醚 |
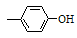 、 、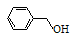 与 与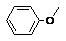 |
|
CnH2n +1NO2 |
硝基烷、氨基酸 |
CH3CH2-NO2与H2N CH2-COOH |
|
Cn(H2O)m |
单糖或二糖 |
葡萄糖与果糖、蔗糖与麦芽糖 |
2、 半径为R的透明薄圆柱体,割去1/4,如图所示,一束平行光与OA、OB成450角射到OA、OB面上,透明体的折射率为
半径为R的透明薄圆柱体,割去1/4,如图所示,一束平行光与OA、OB成450角射到OA、OB面上,透明体的折射率为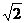 ,光由透明体射向空气发生全反射的临界角为450。若进入透明体的光线射到曲面上,在有折射光线的情况下,不考虑反射光线,则光线从透明体的哪个部分射出,画出射出透明体的光线的光路图。
,光由透明体射向空气发生全反射的临界角为450。若进入透明体的光线射到曲面上,在有折射光线的情况下,不考虑反射光线,则光线从透明体的哪个部分射出,画出射出透明体的光线的光路图。
1、
已知铍核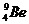 和一个α粒子结合成一个碳核,同时放出5.6兆电子伏的能量。(1)若放出的能量是γ光子,此光子在真空中的波长为多少?(2)若铍核和α粒子共130克,刚好完全反应,那么共放出多少能量?(3)质量亏损共多少千克?
和一个α粒子结合成一个碳核,同时放出5.6兆电子伏的能量。(1)若放出的能量是γ光子,此光子在真空中的波长为多少?(2)若铍核和α粒子共130克,刚好完全反应,那么共放出多少能量?(3)质量亏损共多少千克?
18、 如图所示,P为一面高墙,M为高h=0.8m的矮墙,S为一点光源,三者水平距离如图所示,S以速度V0=10m/s竖直向上抛出,求在落回地面前,矮墙在高墙上的影子消失的时间(g=10m/s2)
如图所示,P为一面高墙,M为高h=0.8m的矮墙,S为一点光源,三者水平距离如图所示,S以速度V0=10m/s竖直向上抛出,求在落回地面前,矮墙在高墙上的影子消失的时间(g=10m/s2)
专题预测:
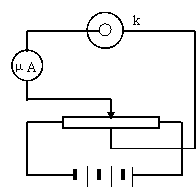
17、图中光电管阴极用极限波长为5000埃的钠制成,现用波长3000埃的光照射阴极,当光电管加正向电压为2.1伏时测得饱和光电流植是0.56微安,求:(1)每秒钟阴极发射的光电子数;(2)光电子到达阳极时的最大动能;(3)变阻器滑动头C与中心固定头O之间电压多大时,微安表读数为零,这时C在O点哪一侧?
16、1905年爱因斯坦提出了著名的质能关系式:E=mc2,其中E是能量,单位为焦耳(J);m是质量,单位是千克(kg);c为光速,单位是米/秒(m/s),质能关系式说明了质量与能量的对应关系,当质量发生变化时,能量也将发生变化,若质量变化为△ m时,对应的能量变化为 △E,则根据质能关系式有△E =△mc2。
太阳等恒星不断向外辐射能量,是以内部质量的减少为代价的,在太阳内部进行着四个氢核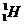 转变成一个氦核
转变成一个氦核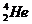 的核聚变反应,发生核聚变反应时释放出一定的能量,并伴随着一定质量的减少,研究表明,1kg氢聚变时发生的质量减少为7×10-3kg,由于只有太阳核心区的高温才足以使氢核产生聚变反应,所以处于太阳核心区的氢才是可利用的,太阳质量为2.0×1030kg,太阳核心区氢的质量约占太阳质量的十分之一,太阳每秒钟向太空辐射4.0×1026J 能量,问:
的核聚变反应,发生核聚变反应时释放出一定的能量,并伴随着一定质量的减少,研究表明,1kg氢聚变时发生的质量减少为7×10-3kg,由于只有太阳核心区的高温才足以使氢核产生聚变反应,所以处于太阳核心区的氢才是可利用的,太阳质量为2.0×1030kg,太阳核心区氢的质量约占太阳质量的十分之一,太阳每秒钟向太空辐射4.0×1026J 能量,问:
(1)太阳每年因向外辐射能量而减少的质量约为多少千克?
(2)太阳已发光了50亿年,估算太阳还能发光多少年?
15、一种用于激光治疗的氦分子激光器,输出337.1nm 波长的激光,激光脉冲的时间约为10 -9s,输出脉冲时的功率为106W,每秒输出的脉冲个数是100个。
(1)这种激光的频率是多少?属于电磁波谱中的哪个波段?
(2)这种激光器的平均输出功率是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com