
第一节:语法和词汇知识(共15小题;每小题1分,满分15分)
21. It’s clear that ________
little money he earns can hardly support ________ family as large as his.
A.the; a B.a; the C.不填;a D.不填;the
22. Children
who have problems connecting letters with sounds or understanding what they
read may be showing ______ of learning disabilities.
A. signs B.
examples C.
symbols D.
marks
23. Was
it in the garden ______ we used to work in ______ the famous actors and
actresses had a picnic?
A. that;
where B. which; that C. where; that D. which; where
24. She went to the bookstore and bought ___________.
A. dozen
of books B. several dozens books
C. several
dozens of books D.
several dozen books
25. ----Henry has
been teaching English in Beijing
University for many years.
----It’s no ______ he can speak Chinese so well and idiomatically.
A. matter B. doubt C. problem D. wonder
26. What
will happen to the child if Jim and Mary ________?
A. break
down B. break up C. break
out D.
break off
27. It
was _________ to be chosen as a torch bearer that he would never forget it.
A. so
great honor B. such great
honor C. so great an honor D. such great an honor
28. He is a nice
neighbor. He often helps us with garden work and is good at speech. ________ he
is quite kind with people.
A. After all B.
Above all C.
First of all D.
In all
29. The
thief ran away when the burglar alarm ________.
A. went
up B.
went off C.
went out D.
went away
30. Most
people think it acceptable to call others by their first name, but some
consider it ________ to use first names without being invited to do so.
A. proper B. properly C. improper D.
improperly
31. ________
I could remember, I did return him the money.
A. As
far as B. As long
as C. As good
as D. As
well as
32. Tom
felt shocked when he saw his Aunty Polly standing in his room with her arms
_______.
A. cross B.
crossing C.
crossed D.
to cross
33. The train goes at 8 o’clock. I’m afraid I can’t ________.
A. make it B.
take it C.
reach for it D.
catch up with it
34. I absolutely
loved the film Angry Sky. The part _______ the hero returns home had me in
floods of tears.
A. that B. which C. where D. when
35. However
hard I tried to think about it, what he said didn’t really __________to me.
A. figure
out B. make out C. turn out D.
get across
21. (本题满分14分)
已知函数f(x)=x2+bsinx-2,(b∈R), F(x)=f(x)+2, 且对于任意实数x,恒有F(x-5)=F(5-x).
(1)求函数f(x)的解析式;
(2)已知函数g(x)=f(x)+2(x+1)+alnx在区间(0,1)上单调, 求实数a的取值范围;
(3)函数 有几个零点?
有几个零点?
解:(1)由题设得:F(x)=x2+bsinx,
∵F(x-5)=F(5-x),
∴F(-x)=F(x)
∴x2-bsinx=x2+bsinx,
∴bsinx=0对于任意实数x都成立,∴b=0
∴f(x)=x2-2.
(2) 由g(x)=f(x)+2(x+1)+alnx=x2+2x+alnx,
得 ,
,
g(x)在(0,1)上恒单调,只需 在(0,1)上恒成立.
在(0,1)上恒成立.
即 2x2+2x+a≥0或2x2+2x+a≤0在(0,1)上恒成立.
∴a≥-(2x2+2x)或a≤-(2x2+2x)在(0,1)上恒成立.
设u(x)=-(2x2+2x), x∈(0,1),易知:u(x)∈(-4,0),
∴a≥0或a≤-4.
(3) 令 ,
,

 ,
,
令 ,列表如下:
,列表如下:
|
x |
 |
-1 |
(-1,0) |
0 |
(0,1) |
1 |
 |
 |
+ |
0 |
- |
0 |
+ |
0 |
- |
|
y |
增 |
 |
减 |
 |
增 |
 |
减 |
∴当k> 时,无零点;
时,无零点;
当k<1或k= 时,有两个零点;
时,有两个零点;
当k=1时,有三个零点;
当 时,有四个零点.
时,有四个零点.
20. (本题满分14分)已知函数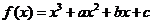 .
.
(Ⅰ)若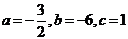 ,求
,求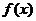 在
在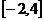 上的最大值与最小值;
上的最大值与最小值;
(Ⅱ)设函数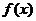 的图像关于原点
的图像关于原点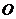 对称,在点
对称,在点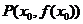 处的切线为
处的切线为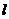 ,
,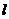 与函数
与函数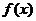 的图像交于另一点
的图像交于另一点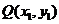 .若
.若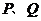 在
在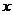 轴上的射影分别为
轴上的射影分别为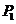 、
、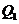 ,
,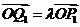 ,求
,求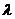 的值.
的值.
(Ⅰ)若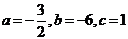 ,
,
|
x |
-2 |
(-2,-1) |
-1 |
(-1,2) |
2 |
(2,4) |
4 |
 |
|
+ |
|
- |
|
+ |
|
|
y |
-1 |
增 |
 |
减 |
-9 |
增 |
17 |
最大值为 最小值为
最小值为

19.(本题满分13分)为应对国际金融危机对企业带来的不良影响,2009年某企业实行裁员增效,已知现有员工a人,每人每年可创纯利润1万元。据评估,在生产条件不变的条件下,每裁员1人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人0.4万元生活费,并且企业正常运行所需人数不得少于现有员工的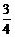 ,设该企业裁员x人后纯收益为y万元.
,设该企业裁员x人后纯收益为y万元.
(1)写出y关于x的函数关系式,并指出x的取值范围;
(2)当140<a≤280时,问企业裁员多少人,才能获得最大的经济效益?(注:在保证能获得最大经济效益的情况下,能少裁员,就尽量少裁)
解:(1)

∵ ,∴
,∴ ,即x的取值范围是
,即x的取值范围是 。
。
(2) ,
,
当140<a≤280时, ,∴当a为偶数时,x取
,∴当a为偶数时,x取 ,y取最大值;;
,y取最大值;;
当a为奇数时,x取 或
或 ,y取最大值.
,y取最大值.
∵尽可能少裁员,,∴x= ,综上所述:当a为偶数时,应裁员
,综上所述:当a为偶数时,应裁员 ,当a为奇数时,应裁员
,当a为奇数时,应裁员 .
.
18. (本题满分13分)已知△ABC的面积S满足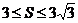 ,且
,且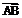 ·
·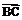 =6,
=6,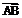 与
与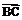 的夹角为
的夹角为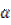 .
.
(1)求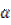 的取值范围;
的取值范围;
(2)若函数f(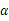 )=sin2
)=sin2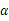 +2sin
+2sin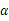 cos
cos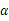 +3cos2
+3cos2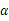 ,求f(
,求f(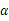 )的最小值,并指出取得最小值时的
)的最小值,并指出取得最小值时的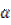 .
.
解: (1)由题意知

由②÷①得=tanθ即3tanθ=S……(3分)
由3≤S≤3得3≤3tanθ≤3……(4分)
又θ为 与
与 的夹角,∴θ∈(0,π)∴θ∈(,)……(6分)
的夹角,∴θ∈(0,π)∴θ∈(,)……(6分)
(2)f(θ)=sin2θ+2sinθcosθ+3cos2θ=1+sin2θ+2cos2θ
∴f(θ)=2+sin2θ+cos2θ=2+sin(2θ+)……(9分)
∵θ∈(,),∴2θ+∈(, )
∴2θ+=,即θ=时,f(θ) min= =……(13分)
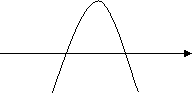
17. (本题满分13分)已知函数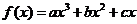 在点
在点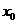 处取得极大值5,其导函数
处取得极大值5,其导函数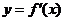 的图象经过点(1,0),(2,0),如图所示, 求:(Ⅰ)
的图象经过点(1,0),(2,0),如图所示, 求:(Ⅰ)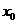 的值; (Ⅱ)a,b,c 的值.
的值; (Ⅱ)a,b,c 的值.
|

|
|
|
|
|
x |
 |
1 |
(1,2) |
2 |
 |
 |
- |
0 |
+ |
0 |
- |
|
y |
减 |
|
增 |
|
减 |
(2) 两根为1,2。
两根为1,2。

16.(13分)已知△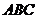 顶点的直角坐标分别为
顶点的直角坐标分别为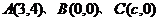 .
.
(1)若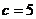 ,求sin∠
,求sin∠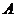 的值; (2)若∠
的值; (2)若∠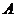 是钝角,求
是钝角,求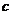 的取值范围.
的取值范围.
解 (1)  ,
,  当c=5时,
当c=5时,
 进而
进而
(2)若A为钝角,则AB﹒AC= -3(c-3)+( -4)2<0 解得c>
显然此时有AB和AC不共线,故当A为钝角时,c的取值范围为[ ,+
,+ )
)
13、 6 14、  15、
15、 
11、
 12、
12、 
21. (本题满分14分)
已知函数f(x)=x2+bsinx-2,(b∈R), F(x)=f(x)+2, 且对于任意实数x,恒有F(x-5)=F(5-x).
(1)求函数f(x)的解析式;
(2)已知函数g(x)=f(x)+2(x+1)+alnx在区间(0,1)上单调, 求实数a的取值范围;
(3)函数 有几个零点?
有几个零点?
厦外2010届高三数学第一阶段测试卷(第Ⅱ卷)2009年10月
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com