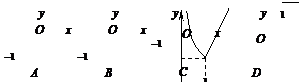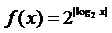2.函数的图像大致是( 　)

1.设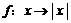是集合A到集合B的映射．若，则(　　 )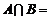

A．{0, 3}　 　　　 B．{0}　　　　　 C．{3}　　　 D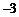．{，0}

3．指数函数、对数函数在考古中的应用．

作业:习题3-5　 B组1,2,3,4

2．对数函数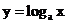,当底数a>1时和当0<a<1时, a的变化对函数图像有何影响?

_____________________________________________________________________________________________________________________________________________________-

4．练习:1

[实际应用]．人们早就发现放射性物质的衰减现象,在考古工作中,常用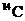的含量来确定有机物的年代．已知放射性物质的衰减服从指数规律: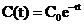,其中t表示衰减的时间,表示放射性物质的原始质量,表示经衰减了t年后剩余的质量．

为计算衰减的年代,通常给出该物质质量衰减一半的时间,称其为该物质的半衰期, 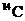的半衰期大约是5730年,由此可确定系数r,人们又知道,放射性物质的衰减速度与其质量成正比的．

1950年在巴比伦发现一根刻有Hammmurbi王朝字样的木炭,当时测定,其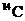分子的衰减速度为4．09个/(g·min),而新砍伐烧成的木炭中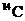的衰减速度为6．68个/(g·min),,请估算出Hammmurbi王朝所在的年代．

解:

课堂小结:1．互为反函数的图像之间的关系________________________________．

3．仿照前面的方法,请你猜想,对数函数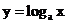当0<a<1时, a的变化对函数图像有何影响?

结论:______________________________________________________________________

2．对数函数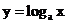,当底数a>1时,a的变化对函数图像有何影响?

结论:______________________________________________________________________

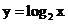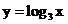
1．根据表中的数据(精确到0．01),画出函数,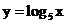的图像,并观察图像,说明三个函数图像的相同与不同之处．

	…	0．5	1	1．5	2	3	4	…	1000	…
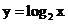
	…	-1	0	0．58	1	1．58	2	…	9．97	…
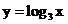
	…	-0．63	0	0．37	0．63	1	1．26	…	6．29	…
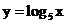
	…	-0．43	0	0．25	0．43	0．68	0．86	…	4．29	…

3．比较下列各题中两个数的大小:

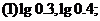
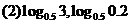
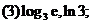
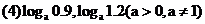
[互动过程2]

观察在同一坐标系内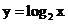函数与函数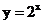的图像，分析它们之间的关系．

解:从图上可以看出点P(a,b)与点_____________关于直线_________对称,函数_______________与函数________________互为反函数,对应于函数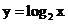图像上任意一点P(a,b),P关于直线y=x的对称点___________总在函数_____________-的图像上,所以,函数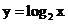的图像与函数____________的图像关于直线_____________对称．

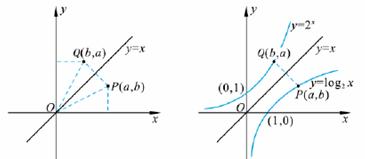
[结论]:__________________________________________________________________

[互动过程3]

2．求下列函数的定义域: