
21. (本小题满分12分)已知等差数列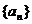 的公差为2,其前n项和
的公差为2,其前n项和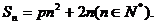
(I)求p的值及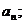
(II)若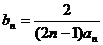 ,记数列
,记数列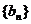 的前n项和为
的前n项和为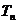 ,求使
,求使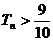 成立的最小正整数n的值。
成立的最小正整数n的值。
请在下面三题中任选一题做答,如果多做,则按所做的第一题记分.
20. (本小题满分12分)已知椭圆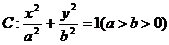 过点
过点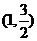 ,且离心率
,且离心率 。
。
(1)求椭圆方程;
(2)若直线 与椭圆交于不同的两点
与椭圆交于不同的两点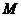 、
、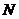 ,且线段
,且线段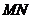 的垂直平分线过定点
的垂直平分线过定点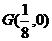 ,求
,求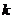 的取值范围。
的取值范围。
19. (本小题满分12分) 如图,平面ABDE⊥平面ABC,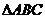 是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD//AE,BD⊥BA,
是等腰直角三角形,AC=BC=4,四边形ABDE是直角梯形,BD//AE,BD⊥BA,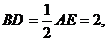 O、M分别为CE、AB的中点
O、M分别为CE、AB的中点
(I)求证:OD//平面ABC;
(II)求直线CD和平面ODM所成角的正弦值;
(III)能否在EM上找一点N,使得ON⊥平面ABDE?若能,请指出点N的位置,并加以证明;若不能,请说明理由。
18. (本小题满分12分) 在锐角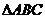 中,已知内角
中,已知内角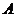 、
、 、
、 所对的边分别为
所对的边分别为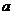 、
、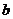 、
、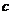 ,向量
,向量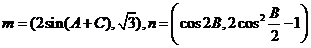 ,且向量
,且向量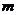 ,
,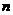 共线。
共线。
(1)求角 的大小;
的大小;
(Ⅱ)如果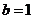 ,求
,求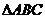 的面积
的面积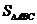 的最大值。
的最大值。
17.(本小题满分12分)某商场搞促销,当顾客购买商品的金额达到一定数量之后方可抽奖,
根据顾客购买商品的金额,从箱中(装有4个红球,3只白球,且除颜色外,球的外部特征完全
相同)每抽到一只红球奖励20元代金券,每抽到一只白球奖励10元代金券(当顾客通过抽奖
确定获得的代金券金额后,即将小球全部放回箱中)
(1)当顾客购买金额超过500元而少于1000元(含1000)时,可从箱中一次随机抽取3个小球,求其中至少有一个红球的概率.
(2)当顾客购买金额超过1000元时,可从箱中一次随机抽取4个小球,设他所获代金券金额为ξ元,求ξ的概率分布列和数学期望
16. 考察等式: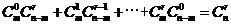 (*)
(*)
其中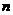 、
、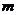 、
、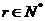 ,
,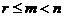 且
且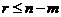 。
。
某同学用概率论方法证明等式(*)如下:
设一批产品共有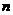 件,其中
件,其中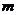 件是次品,其余为正品。现从中随机取出
件是次品,其余为正品。现从中随机取出 件产品,记事件
件产品,记事件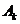 =
=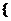 取到的r件产品中恰有k件次品
取到的r件产品中恰有k件次品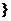 ,则
,则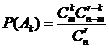 ,
,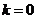 ,1,…,
,1,…, 。显然
。显然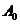 ,
,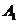 ,…,
,…,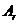 为互斥事件,且
为互斥事件,且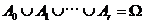 (必然事件),因此
(必然事件),因此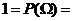
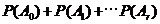 =
= ,所以
,所以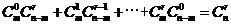 ,即等式(*)成立。
,即等式(*)成立。
对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑。
现有以下四个判断:
①等式(*)成立; ②等式(*)不成立 ③证明正确; ④证明不正确
试写出所有正确判断的序号  。
。
15.若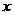 、
、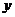 满足
满足 ,则
,则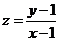 的最大值是
。
的最大值是
。
14.过一定点的互相垂直的两条直线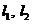 与圆锥曲线
与圆锥曲线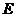 分别交于点A、B和C、D,如果线段AB的中点的横坐标为
分别交于点A、B和C、D,如果线段AB的中点的横坐标为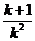 (
(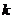 为直线
为直线 的斜率),则线段CD的中点的横坐标为
.
的斜率),则线段CD的中点的横坐标为
.
13. 为了了解“预防禽流感疫苗”的使用情况,温州市卫生部门对本地区9月份至11月份使用疫苗的所有养鸡场进行了调查,根据下列图表提供的信息,可以得出这三个月本地区每月注射了疫苗的鸡的数量平均为 万只.
 |
||||||||||
|
||||||||||
12.已知直线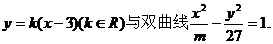 某学生作了如下变形:由
某学生作了如下变形:由 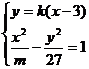 消去y后得到形如
消去y后得到形如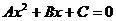 的方程,当A=0时,该方程有一解;当A≠0时,
的方程,当A=0时,该方程有一解;当A≠0时,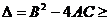 恒成立.假设学生的演算过程是正确的,则实数m的取值范围为
恒成立.假设学生的演算过程是正确的,则实数m的取值范围为
|
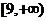 B.
B.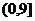 C.
C.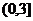 D.
D.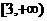
第Ⅱ卷(非选择题 共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com