9、2005年底，某地区经济调查队对本地区居民收入情况进行抽样调查，抽取1000户，按

本地区在“十一五”规划中明确

提出要缩小贫富差距，到2010年

要实现一个美好的愿景，由右边圆图显示，则中等收入家庭的数

量在原有的基础要增加的百分比和低收入家庭的数量在原有的基

础要降低的百分比分别为　　　　　　　　　　　　 　(　 B　　 )

A．25% , 27.5%　　 B．62.5% , 57.9%　　 C．25% , 57.9%　　 D．62.5%,42.1%

8、已知等比数列{a_n}的前n项和为S_n.

　　 (Ⅰ)若S_m，S_m+2，S_m+1成等差数列，证明a_m，a_m+2，a_m+1成等差数列；

　　 (Ⅱ)写出(Ⅰ)的逆命题，判断它的真伪，并给出证明.

　　 证 (Ⅰ) ∵S_m+1＝S_m+a_m+1，S_m+2＝S_m+a_m+1+a_m+2．

由已知2S_m+2＝S_m+S_m+1，∴ 2(S_m+a_m+1+a_m+2)＝S_m+(S_m+a_m+1)，

∴a_m+2＝－a_m+1，即数列{a_n}的公比q＝－.

　 　∴a_m+1＝－a_m，a_m+2＝a_m，∴2a_m+2＝a_m+a_m+1，∴a_m，a_m+2，a_m+1成等差数列.

　　 (Ⅱ) (Ⅰ)的逆命题是：若a_m，a_m+2，a_m+1成等差数列，则S_m，S_m+2，S_m+1成等差数列.

　　 设数列{a_n}的公比为q，∵a_m+1＝a_mq，a_m+2＝a_mq²．

由题设，2a_m+2＝a_m+a_m+1，即2a_mq²＝a_m+a_mq，即2q²－q－1＝0，∴q＝1或q＝－.

　　 当q＝1时，A≠0，∴S_m， S_m+2， S_m+1不成等差数列.

逆命题为假.

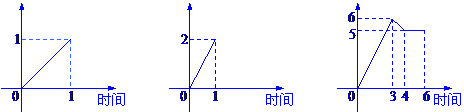
7、一水池有2个进水口,1个出水口,一个口进出水速度如图甲、乙所示.某天0点到6点,

该水池的蓄水量如图丙所示(至少打开一个水口),给出以下3个论断：

　进水量　　　　　　　　　 出水量　　　　　　　　　 蓄水量

　 甲　　　　　　　　　　　 乙　　　　　　　　　　　 丙

(1)0点到3点只进水不出水；(2)3点到4点不进水只出水；(3)4点到6点不进水不

出水。则一定不确定的论断是　　　　　 (把你认为是符合题意的论断序号都填上)。

答案：(2)(3)

6、直角坐标系中横坐标、纵坐标均为整数的点称为格点，如果函数f(x)的图象恰好通过k(k∈N*)个格点，则称函数f(x)为k阶格点函数。下列函数：

①　　 f(x)=sinx；　 ②f(x)=π(x－1)²+3；　 ③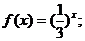　 ④，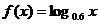

其中是一阶格点函数的有　　　　　 　.　 答案：①②④

5、用水清洗一堆蔬菜上残留的农药的效果假定如下：用x单位量的水清洗一次以后，蔬菜上残留的农药量与这次清洗前残留的农药量之比为．

(Ⅰ)试解释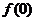的实际意义；

(Ⅱ)现有a(a＞0)单位量的水，可以清洗一次，也可以把水平均分成2份后清洗两次．哪种方案清洗后蔬菜上残留的农药比较少？请说明理由．

答案：解：(I)f(0)=1．表示没有用水清洗时，蔬菜上的农药量没有变化．……………2＇

　 (Ⅱ)设清洗前蔬菜上的农药量为1，那么用a单位量的水清洗1次后．残留的农药量为 W₁=1×f(a)=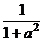；……………………………………………………………………4＇

又如果用单位量的水清洗1次，残留的农药量为1×f()=，

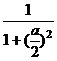此后再用单位量的水清洗1次后，残留的农药量为

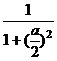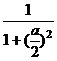W₂=·f()=[]²=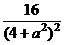．……………………………8＇

由于W₁－W₂=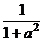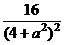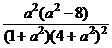－=，………………………9＇

故当a>2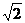时，W₁>W₂，此时，把a单位量的水平均分成2份后，清洗两次，残留的农药量较少；当a=2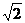时，W₁=W₂，此时，两种清洗方式效果相同；当a<2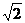时，W₁<W₂，此时，把a单位量的水清洗一次，残留的农药量较少．…………………………12＇

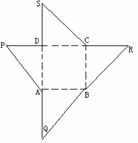
4、如图为一几何体的的展开图，其中ABCD是边长

为6的正方形，SD=PD＝6，CR=SC，AQ=AP，点S,

D,A,Q及P,D,C,R共线，沿图中虚线将它们折叠起来，

使P，Q，R，S四点重合，则需要　　　　 个这样的

几何体，可以拼成一个棱长为6的正方体。　 答案：3

3、在算式“2×□+1×□=30”的两个口中，分别填入两个自然数，使它们的倒数之和最小，则这两个数应分别为　　　　　 和　　　　 .　 答案：9，12.

2、设M是由满足下列条件的函数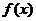构成的集合：“①方程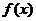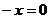有实数根；②

函数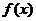的导数满足.”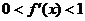

　 (I)判断函数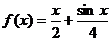是否是集合M中的元素，并说明理由；

　 (II)集合M中的元素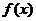具有下面的性质：若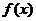的定义域为D，则对于任意

[m，n]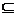D，都存在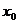[m，n]，使得等式成立”，

试用这一性质证明：方程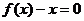只有一个实数根；

　 (III)设是方程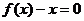的实数根，求证：对于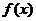定义域中任意的.

解：(1)因为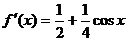，…………2分　

　　　　 所以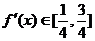满足条件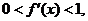………………3分

　　　　 又因为当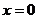时，，所以方程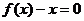有实数根0.

　　　　 所以函数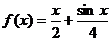是集合M中的元素.…………4分

　　 (2)假设方程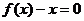存在两个实数根)，

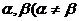　　　　 则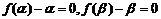，………5分　 不妨设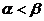，根据题意存在数

　　　　 使得等式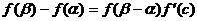成立，……………………7分

　　　　 因为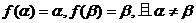，所以，

　　　　 与已知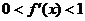矛盾，所以方程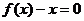只有一个实数根；…………9分

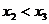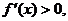　　　　 (3)不妨设，因为所以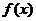为增函数，所以，

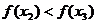　　　　 又因为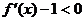，所以函数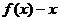为减函数，………………10分

　　　　 所以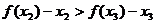，…………11分

　　　　 所以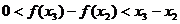，即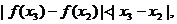…………12分

　　　　 所以

…………………………13分

1、为研究“原函数图象与其反函数图象的交点是否在直线上”这个课题，我们可以分三步进行研究：

　　 (I)首先选取如下函数：

　　 ，，

　　 求出以上函数图象与其反函数图象的交点坐标：

　　 与其反函数的交点坐标为(－1，－1)

　　 与其反函数的交点坐标为(0，0)，(1，1)

　　 与其反函数的交点坐标为()，(－1，0)，(0，－1)

　　 (II)观察分析上述结果得到研究结论；

　 　(III)对得到的结论进行证明。

　　 现在，请你完成(II)和(III)。

解：(II)原函数图象与其反函数图象的交点不一定在直线y＝x上　　　　　　　　 2分

　　 (III)证明：设点(a，b)是的图象与其反函数图象的任一交点，由于原函数与反函数图象关于直线y＝x对称，则点(b，a)也是的图象与其反函数图象的交点，且有

　　 若a＝b时，交点显然在直线上

　　 若a<b且是增函数时，有，从而有b<a，矛盾；若b<a且是增函数时，有，从而有a<b，矛盾

　 　若a<b且是减函数，有，从而a<b成立，此时交点不在直线y＝x上；同理，b<a且是减函数时，交点也不在直线y＝x上。

　　 综上所述，如果函数是增函数，并且的图象与其反函数的图象有交点，则交点一定在直线上；

　　 如果函数是减函数，并且的图象与其反函数的图象有交点，则交点不一定在直线y＝x上。　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 14分

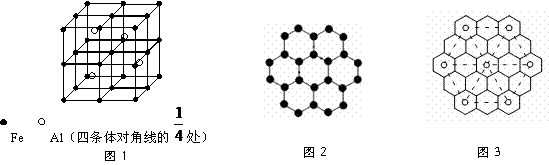
9． ⑴一种Al－Fe合金的立体晶胞如图1所示。确定该合金的化学式____________。用N_A表示阿伏加德罗常数，则晶胞质量的计算式是_________________，若晶胞的边长＝a nm，则此合金密度的计算式是________________g/cm³。

⑵石墨的层状结构如下图2所示，图中7个六元环实际占有的碳原子数是　　　　 ，若该层状结构可由很多个平行四边形无隙并置得到，每个平行四边形实际占有2个碳原子，请在图中画出一个这样的平行四边形。

⑶石墨能与熔融金属钾作用，形成蓝色的C₂₄K、灰色的C₄₈K、C₆₀K等。有一种青铜色的C_xK中K原子(用o表示)的分布如图3所示，则x=　　　　 ；另有一种石墨化合物C₃₂K，其中K原子的分布也类似图的正六边形，该正六边形的边长是上右图中正六边形边长的　　　　 倍。