
20. (本小题16分)
函数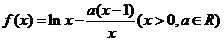 。
。
(1)试求 的单调区间;
的单调区间;
(2)当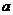 >0时,求证:函数
>0时,求证:函数 的图像存在唯一零点的充要条件是
的图像存在唯一零点的充要条件是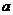 =1;
=1;
(3)求证:不等式 对于
对于 恒成立。
恒成立。
友情提示:请细心做题,祝同学们考试顺利!
编写寄语: 即将进入最后冲刺阶段,希望这些试卷能给同学们有所帮助。
此次出卷老师再次提醒同学们: 细心是成功的基础,慎密是成功的阶梯!
相信自己,因为:一、你们是海安学子;二、你们的老师已经帮你们作了全面细致的复习!
真诚祝愿: 2010届高三的所有同学个个心想事成!
考上理想的大学! 成就自己辉煌人生!
19. (本小题16分)如图:设一正方形纸片 边长为
边长为 ,从此纸片中裁剪出一个正方形和四个全等的等腰三角形,恰好能做成一个正四棱锥(粘接损耗不计),图中
,从此纸片中裁剪出一个正方形和四个全等的等腰三角形,恰好能做成一个正四棱锥(粘接损耗不计),图中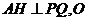 为正四棱锥底的中心
为正四棱锥底的中心
(1)若正四棱锥得棱长都相等,求这个正四棱锥的体积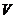 ;
;
(2)设等腰三角形底角为 ,试把正四棱锥侧面积
,试把正四棱锥侧面积 表示为
表示为 的函数,并求
的函数,并求 的范围
的范围

|
18.(本小题15分)已知等差数列{an}中,首项a1=1,公差d为整数,且满足a1+3<a3,
a2+5>a4,数列{bn}满足 ,其前n项和为Sn.
,其前n项和为Sn.
(1)求数列{an}的通项公式an;
(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.
17. (本小题15分)如图, 的三个顶点坐标分别为
的三个顶点坐标分别为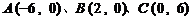 ,
, 分别是高
分别是高 的两个三等分点,过
的两个三等分点,过 作直线
作直线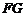 ∥
∥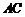 ,分别交
,分别交 和
和 于
于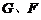 ,连接
,连接 .
.
(Ⅰ)求过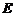 、
、 、
、 三点的圆
三点的圆 的方程;
的方程;
 (Ⅱ)在线段
(Ⅱ)在线段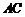 上是否存在点
上是否存在点 ,使得过点
,使得过点 存在和圆M相切的直线,并且若过点
存在和圆M相切的直线,并且若过点 存在两条切线时,则点
存在两条切线时,则点 和两切点
和两切点 组成的
组成的 ?若存在,求出
?若存在,求出 点对应轨迹的长度;若不存在,试说明理由.
点对应轨迹的长度;若不存在,试说明理由.
|
16. (本小题14分)如图,在四棱锥
(本小题14分)如图,在四棱锥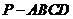 中,
中,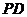 垂直于正方形
垂直于正方形 所在的平,
所在的平, 分别是
分别是 的中点;
的中点;
(1) 求证: //平面
//平面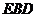
(2) 求证:平面 平面
平面
|
15.(本小题14分)在 中,内角
中,内角 对边的边长分别是
对边的边长分别是 ,且满足
,且满足 ,
, 。
。
(1) 时,若
时,若 ,求
,求 的面积.
的面积.
(2)求 的面积等于
的面积等于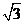 的一个充要条件。
的一个充要条件。
14. 曲边梯形由曲线 所围成,过曲线
所围成,过曲线 上一点P作切线,使得此切线从曲边梯形上切出一个面积最大的普通梯形,这时点P的坐标是_ _▲____.
上一点P作切线,使得此切线从曲边梯形上切出一个面积最大的普通梯形,这时点P的坐标是_ _▲____.
13. 设等差数列 的首项及公差均是正整数,前
的首项及公差均是正整数,前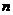 项和为
项和为 ,
,
且 ,
, ,
, ,则
,则 =_ ▲__
_.
=_ ▲__
_.
12. 如图所示的流程图输出的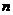 值是_ _▲____.
值是_ _▲____.
11. (改编)当 时,
时,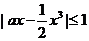 恒成立,则
恒成立,则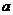 的取值范围是__▲__.
的取值范围是__▲__.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com