
9、对于集合N={1, 2, 3,…, n}及其它的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减、加后继的数。例如集合{1, 2, 4, 6, 9}的交替和是9–6+4–2+1=6,集合{5}的交替和为5。当集合N中的n=2时,集合N={1, 2}的所有非空子集为{1},{2},{1, 2},则它的“交替和”的总和S2=1+2+(2–1)=4,请你尝试对n=3、n=4的情况,计算它的“交替和”的总和S3、S4,并根据其结果猜测集合N={1, 2, 3,…, n}的每一个非空子集的“交替和”的总和Sn= n .2n–1 。(不必给出证明)
8、已知两个向量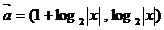 ,
,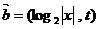
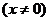 .
.
(1)若t=1且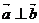 ,求实数x的值;
,求实数x的值;
(2)对tÎR写出函数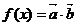 具备的性质.
具备的性质.
解:(1)由已知得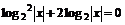 ……2分
……2分
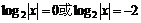 ……4分
……4分
解得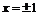 ,或
,或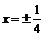 ……6分
……6分
(2)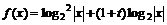 ……8分
……8分
具备的性质:
①偶函数;
②当 即
即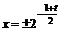 时,
时, 取得最小值
取得最小值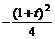 (写出值域为
(写出值域为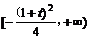 也可);
也可);
③单调性:在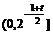 上递减,
上递减,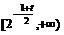 上递增;由对称性,在
上递增;由对称性,在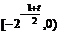 上递增,在
上递增,在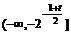 递减
……14分
递减
……14分
说明:写出一个性质得3分,写出两个性质得5分,写出三个性质得6分,包括写出函数的零点(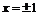 ,
, )等皆可。写出函数的定义域不得分,写错扣1分
)等皆可。写出函数的定义域不得分,写错扣1分
1、a1、a2、a3、a4、…a99的“凯森和”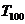 =
991 。
=
991 。
6、有穷数列{an},Sn为其前n项和,定义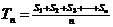 为数列{an}的“凯森和”,
为数列{an}的“凯森和”,
如果有99项的数列a1、a2、a3、…、a99的“凯森和”为1000,则有100项的数列
5、(理)已知
 为正常数。
为正常数。
(1)可以证明:定理“若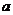 、
、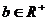 ,则
,则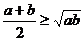 (当且仅当
(当且仅当 时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);
时取等号)”推广到三个正数时结论是正确的,试写出推广后的结论(无需证明);
(2)若 在
在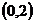 上恒成立,且函数
上恒成立,且函数 的最大值大于
的最大值大于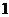 ,求实数
,求实数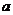 的取值范围,并由此猜测
的取值范围,并由此猜测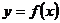 的单调性(无需证明);
的单调性(无需证明);
(3)对满足(2)的条件的一个常数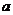 ,设
,设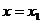 时,
时, 取得最大值。试构造一个定义在
取得最大值。试构造一个定义在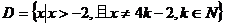 上的函数
上的函数 ,使当
,使当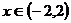 时,
时,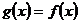 ,当
,当 时,
时, 取得最大值的自变量的值构成以
取得最大值的自变量的值构成以 为首项的等差数列。
为首项的等差数列。
解:(1)若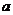 、
、 、
、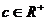 ,则
,则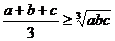 (当且仅当
(当且仅当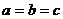 时取等号)。
时取等号)。
(2)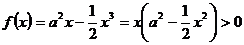 在
在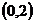 上恒成立,即
上恒成立,即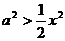 在
在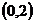 上恒成立,
上恒成立,
∵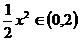 ,∴
,∴ ,即
,即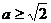 ,
,
又∵
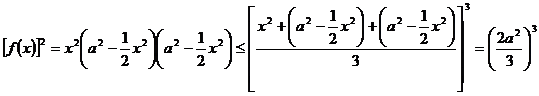 ∴
∴ ,即
,即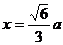 时,
时,
 ,
,
又∵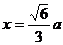
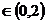 ,∴
,∴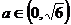 。
综上,得
。
综上,得 。
。
易知, 是奇函数,∵
是奇函数,∵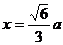 时,函数有最大值,∴
时,函数有最大值,∴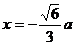 时,函数有最小值。
时,函数有最小值。
故猜测: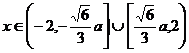 时,
时, 单调递减;
单调递减;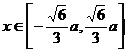 时,
时, 单调递增。
单调递增。
(3)依题意,只需构造以 为周期的周期函数即可。
为周期的周期函数即可。
如对 ,
, ,此时
,此时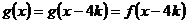 ,
,
即 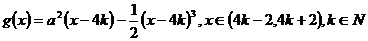 。
。
(文)已知函数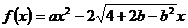 ,
,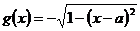 ,
,
(Ⅰ)当 时,若
时,若 在
在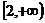 上单调递增,求
上单调递增,求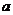 的取值范围;
的取值范围;
(Ⅱ)求满足下列条件的所有实数对 :当
:当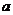 是整数时,存在
是整数时,存在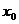 ,使得
,使得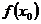 是
是 的最大值,
的最大值, 是
是 的最小值;
的最小值;
(Ⅲ)对满足(Ⅱ)的条件的一个实数对 ,试构造一个定义在
,试构造一个定义在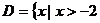 ,且
,且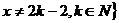 上的函数
上的函数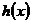 ,使当
,使当 时,
时,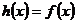 ,当
,当 时,
时,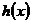 取得最大值的自变量的值构成以
取得最大值的自变量的值构成以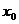 为首项的等差数列。
为首项的等差数列。
解:(Ⅰ)当 时,
时,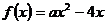 ,
,
若 ,
, ,则
,则 在
在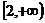 上单调递减,不符题意。
上单调递减,不符题意。
故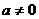 ,要使
,要使 在
在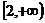 上单调递增,必须满足
上单调递增,必须满足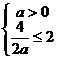 ,∴
,∴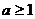 。
。
(Ⅱ)若 ,
,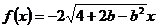 ,则
,则 无最大值,故
无最大值,故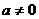 ,∴
,∴ 为二次函数,
为二次函数,
要使 有最大值,必须满足
有最大值,必须满足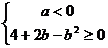 ,即
,即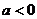 且
且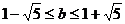 ,
,
此时,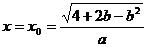 时,
时, 有最大值。
有最大值。
又 取最小值时,
取最小值时,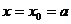 ,依题意,有
,依题意,有 ,则
,则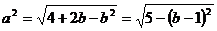 ,
,
∵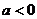 且
且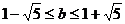 ,∴
,∴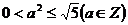 ,得
,得 ,此时
,此时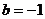 或
或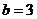 。
。
∴满足条件的实数对 是
是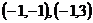 。
。
(Ⅲ)当实数对 是
是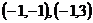 时,
时,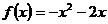
依题意,只需构造以2(或2的正整数倍)为周期的周期函数即可。
如对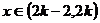 ,
,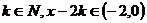 ,
,
此时,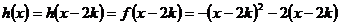 ,
,
故 。
。
4、(12′=9′+3′)(理)设 表示幂函数
表示幂函数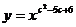 在
在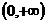 上是增函数的
上是增函数的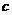 的集合;
的集合; 表示不等式
表示不等式 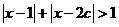 对任意
对任意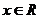 恒成立的
恒成立的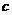 的集合。(1)求
的集合。(1)求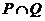 ;(2)试写出一个解集为
;(2)试写出一个解集为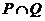 的不等式。
的不等式。
(文)设 表示幂函数
表示幂函数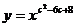 在
在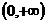 上是增函数的
上是增函数的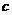 的集合;
的集合; 表示不等式
表示不等式 对任意
对任意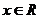 恒成立的
恒成立的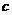 的集合。(1)求
的集合。(1)求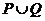 ;(2)试写出一个解集为
;(2)试写出一个解集为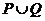 的不等式。
的不等式。
解:(理)(1)∵幂函数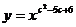 在
在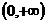 上是增函数,∴
上是增函数,∴ ,即
,即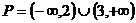 ,
,
又不等式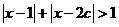 对任意
对任意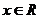 恒成立,∴
恒成立,∴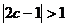 ,即
,即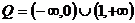 ,
,
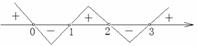 ∴
∴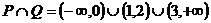 。
。
(2)一个解集为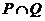 的不等式可以是
的不等式可以是
 。
。
(文)(1)∵幂函数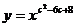 在
在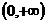 上是增函数,∴
上是增函数,∴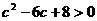 ,即
,即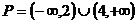 ,
,
又不等式 对任意
对任意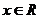 恒成立,∴
恒成立,∴ ,即
,即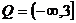 ,
,
∴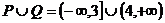 。
。
(2)一个解集为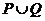 的不等式可以是
的不等式可以是
 。
。
3、已知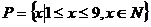 ,记
,记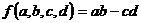 ,(其中
,(其中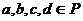 ),例如:
),例如: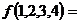
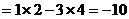 。设
。设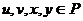 ,且满足
,且满足 ,则有序数组
,则有序数组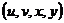
是
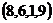 。
。 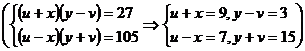
2、用锤子以均匀的力敲击铁钉入木板。随着铁钉的深入,铁钉所受的阻力会越来越大,使得每次钉入木板的钉子长度后一次为前一次的 。已知一个铁钉受击
。已知一个铁钉受击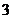 次后全部进入木板,且第一次受击后进入木板部分的铁钉长度是钉长的
次后全部进入木板,且第一次受击后进入木板部分的铁钉长度是钉长的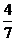 ,请从这个实事中提炼出一个不等式组是
,请从这个实事中提炼出一个不等式组是
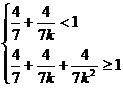 。
。
1、已知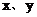 之间满足
之间满足
(1)方程 表示的曲线经过一点
表示的曲线经过一点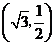 ,求b的值
,求b的值
(2)动点(x,y)在曲线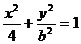 (b>0)上变化,求x22y的最大值;
(b>0)上变化,求x22y的最大值;
(3)由 能否确定一个函数关系式
能否确定一个函数关系式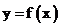 ,如能,求解析式;如不能,再加什么条件就可使
,如能,求解析式;如不能,再加什么条件就可使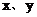 之间建立函数关系,并求出解析式。
之间建立函数关系,并求出解析式。
解:(1) (4分)
(4分)
(2)根据 得
得 (5分)
(5分)
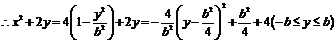 (7分)
(7分)
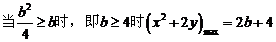

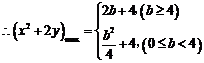 (10分)
(10分)
(2)不能 (11分)
如再加条件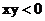 就可使
就可使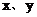 之间建立函数关系
(12分)
之间建立函数关系
(12分)
解析式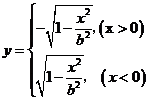 (14分)
(14分)
(不唯一,也可其它答案)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com