
3.若 ,
,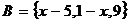 ,
,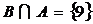 ,求
,求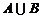
解,由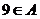 ,可得
,可得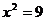 或
或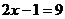 ,解得
,解得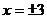 或5
或5
当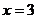 时,
时,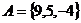 ,
,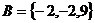 ,
,
集合B中元素违反互异性,故舍去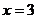
当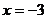 时,
时,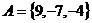 ,
,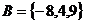 ,
,
满足题意,此时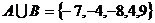
当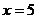 时,
时,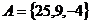 ,
,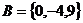 ,
,
此时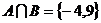 ,这与
,这与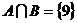 矛盾,故
矛盾,故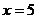 舍去,
舍去,
综上知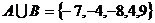 .
.
2.已知全集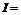 {
{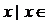 R},集合
R},集合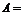 {
{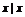 ≤1或
≤1或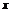 ≥3},集合
≥3},集合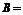 {
{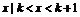 ,
,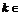 R},且
R},且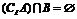 ,则实数
,则实数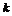 的取值范围是 (
A )
的取值范围是 (
A )
(A)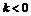 或
或 (B)
(B)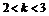
(C)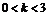 (D)
(D)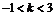
1.下列表示图形中的阴影部分的是( A )
A
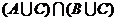 B
B
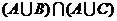
C
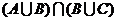 D
D
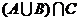
例1、已知全集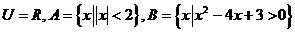 ,则
,则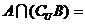 ( )
( )
A.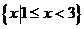 B.
B.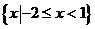

C.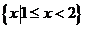 D.
D.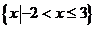

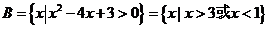
 解析:
解析:
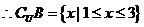
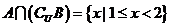 , 故选C
, 故选C
答案:C
例2、已知集合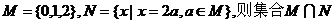 等于( )
等于( )
A.{0} B .{0,2} C.{1,2} D.{0,1}
.{0,2} C.{1,2} D.{0,1}
解析:由已知得集合N={0,2,4},所以集合M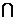 N={0,2},故选B
N={0,2},故选B
答案:B
例3、设 A={(x,y)|y=-4x+6},
B={(x,y)|y=3x-8},则A∩B等于( )
(A){(2,-1)} (B){(2,-2)}
(C){(3,-1)} (D){(4,-2)}
分析:这是一道考查集合运算的试题,注意到集合A与集合B中的代表元素(x,y),表示一次函数图象上的点即直线上的点,因此,求集合A与集合B的交集,应转化为求两条直线的交点,体现了数学上的转化与化归的思想。
解:依题意,应求直线y=-4x+6与y=3x-8的交点,将它们联立方程组,解得交点坐标为(2,-2),故选(B)。
答案:B
例4.设全集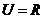 ,
,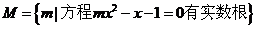 ,
,
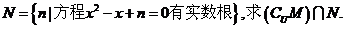
分析:方程有实根的条件是要看方程的类型,如果是二次,则判别式非负,如果是一次则有实根.如果不确定则需要分类讨论.确定了集合再进行交并补的运算.
解:当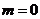 时,
时,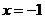 ,即
,即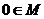 ;
;
当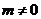 时,
时, 即
即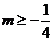 ,且
,且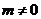
∴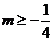 ,∴
,∴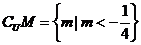
而对于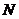 ,
, 即
即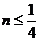 ,∴
,∴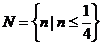
∴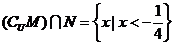

评注:本题要根据方程的类型来确定集合中的元素,利用分类讨论的数学思想解答问题.
例5.已知集合A={x|x2-3x+2=0},B={x|x2-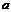 x+
x+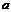 -1=0},且A∪B=A,求
-1=0},且A∪B=A,求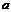 的值.
的值.
分析:集合是确定的集合,由A∪B=A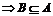 而推出B有四种可能,进而求出
而推出B有四种可能,进而求出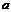 的值.
的值.
解:
∵ A∪B=A, 
∵ A={1,2},∴ B=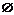 或B={1}或B={2}或B={1,2}.
或B={1}或B={2}或B={1,2}.
若B=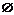 ,则令△<0得
,则令△<0得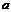 ∈
∈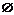 ;
;
若B={1},则令△=0得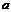 =2,此时1是方程的根;
=2,此时1是方程的根;
若B={2},则令△=0得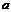 =2,此时2不是方程的根,∴
=2,此时2不是方程的根,∴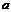 ∈
∈ ;
;
若B={1,2}则令△>0得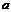 ∈R且
∈R且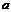 ≠2,把x=1代入方程得
≠2,把x=1代入方程得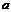 ∈R,把x=2代入方程得
∈R,把x=2代入方程得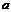 =3.
=3.
综上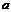 的值为2或3.
的值为2或3.
点评:本题不能直接写出B={1,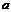 -1},因为
-1},因为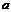 -1可能等于1,与集合元素的互异性矛盾,另外还要考虑到集合B有可能是空集,还有可能是单元素集的情况.
-1可能等于1,与集合元素的互异性矛盾,另外还要考虑到集合B有可能是空集,还有可能是单元素集的情况.
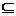
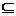 (1)A∩A =A
A∩φ=φ A∩B
A A∩B
B A∩B= B∩A
(1)A∩A =A
A∩φ=φ A∩B
A A∩B
B A∩B= B∩A
(2)A∪A = A A∪φ= A A A∪B
B A∪B A∪B= B∪A
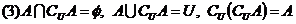
(4)集合的并、交、补的关系
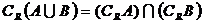

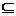 (5) 若A∩B=A,则A B,反之,亦然.
(5) 若A∩B=A,则A B,反之,亦然. 
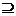 (6) 若A∪B=A,则A B.反之,亦然.
(6) 若A∪B=A,则A B.反之,亦然.
注意:遇此条件首先考虑空集是任何集合的子集
(1)交集:A∩B={x|x∈A且x∈B};
(2)并集:A∪B={x|x∈A或x∈B};
(3)补集:∁uA={x|x∈u且x∈A}
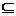 (其中u称为全集,A u)
(其中u称为全集,A u)
3、情感.态度与价值观
学生感受到学习集合后有收获,增强学好数学的信心.
[教学重点]: 复习集合的交、并、补的运算. 
[教学难点]:交、并、补的运算.
[教学教具]:多媒体
[课时安排]: 1课时
[学法指导]:学生通过自主整理、回顾复习. 
[讲授过程]
2、 过程与方法 
(1)、通过例题讲解让学生回顾掌握集合的交、并、补的运算.
(2)、让学生归纳整理本章所学知识使知识形成网络.
[教学目标]
1、知识与技能
(1)、理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集
(2)、理解在给定集合中一个子集的补集的含义,会求给定子集的补集;并会用它们正确表示一些简单的集合.
(3)、能使用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用.
21.(本小题满分14分)
已知函数 当
当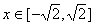 时,总有
时,总有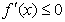 .
.
(1)求函数f(x)的解析式;
(2)设函数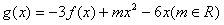 ,求证:当
,求证:当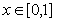 时,若
时,若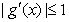 恒成立,
恒成立,
则|g(x)|≤3.5也恒成立.
2010届“三校联考”第二次统一考试
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com