
7、规定a△b=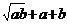 ,a,
b
,a,
b ,若1△k=3,则函数f(x)=k△x的值域为
(1,+¥
)
,若1△k=3,则函数f(x)=k△x的值域为
(1,+¥
)
6、为了保证信息安全传输,有一种称为秘密密钥密码系统,其加密、解密原理如下图:
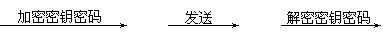
明文 密文 密文 明文,
现在加密密钥为y=loga(x+2),如下所示:明文“6”通过加密后得到密文“3”,
再发送,接受方通过解密密钥解密得明文“6”,问“接受方接到密文”4“,则解密
后得到明文为 14 。
5、⑴证明:当a>1时,不等式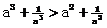 成立。
成立。
⑵要使上述不等式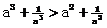 成立,能否将条件“a>1”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由。
成立,能否将条件“a>1”适当放宽?若能,请放宽条件并简述理由;若不能,也请说明理由。
⑶请你根据⑴、⑵的证明,试写出一个类似的更为一般的结论,且给予证明。
解:(1)证: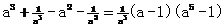 ,∵a>1,∴
,∵a>1,∴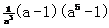 >0,
>0,
∴原不等式成立 (6¢)
(2)∵a-1与a5-1同号对任何a>0且a¹1恒成立,∴上述不等式的条件可放宽
为a>0且a¹1 (9¢)
(3)根据(1)(2)的证明,可推知:若a>0且a¹1,m>n>0,则有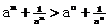 (12¢)
(12¢)
证:左式-右式=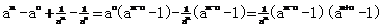 (14¢)
(14¢)
若a>1,则由m>n>0Þam-n>0,am+n>0Þ不等式成立;
若0<a<1,则由m>n>0Þ0<am-n<1, 0<am+n<1Þ不等式成立.(16¢)
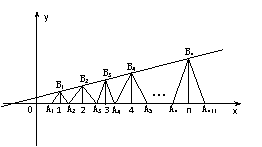
4、已知点列B1(1,y1)、B2(2,y2)、…、Bn(n,yn)(n∈N)
顺次为一次函数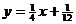 图象上的点,
图象上的点,
点列A1(x1,0)、A2(x2,0)、…、An(xn,0)(n∈N)
顺次为x轴正半轴上的点,其中x1=a(0<a<1),
对于任意n∈N,点An、Bn、An+1构成以
Bn为顶点的等腰三角形。
⑴求{yn}的通项公式,且证明{yn}是等差数列;
⑵试判断xn+2-xn是否为同一常数(不必证明),并求出数列{xn}的通项公式;
⑶在上述等腰三角形AnBnAn+1中,是否存在直角三角形?若有,求出此时a值;若不存在, 请说明理由。
解:(1)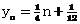 (nÎN),yn+1-yn=
(nÎN),yn+1-yn=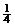 ,∴{yn}为等差数列 (4¢)
,∴{yn}为等差数列 (4¢)
(2)xn+1-xn=2为常数 (6¢) ∴x1,x3,x5,…,x2n-1及x2,x4,x6,,…,x2n都是公差为2的等差数列,
∴x2n-1=x1+2(n-1)=2n-2+a,x2n=x2+2(n-1)=2-a+2n-2=2n-a,
∴xn=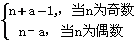 (10¢)
(10¢)
(3)要使AnBnAn+1为直角三形,则 |AnAn+1|=2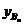 =2(
=2(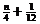 )Þxn+1-xn=2(
)Þxn+1-xn=2(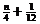 )
)
当n为奇数时,xn+1=n+1-a,xn=n+a-1,∴xn+1-xn=2(1-a).
Þ2(1-a)=2(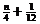 ) Þa=
) Þa=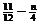 (n为奇数,0<a<1) (*)
(n为奇数,0<a<1) (*)
取n=1,得a=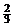 ,取n=3,得a=
,取n=3,得a=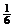 ,若n≥5,则(*)无解; (14¢)
,若n≥5,则(*)无解; (14¢)
当偶数时,xn+1=n+a,xn=n-a,∴xn+1-xn=2a.
∴2a=2(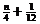 )Þa=
)Þa=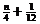 (n为偶数,0<a<1) (*¢),取n=2,得a=
(n为偶数,0<a<1) (*¢),取n=2,得a=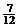 ,
,
若n≥4,则(*¢)无解.
综上可知,存在直角三形,此时a的值为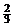 、
、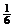 、
、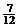 .
(18¢)
.
(18¢)
3、在数学拓展课上,老师规定了一种运算:a*b=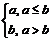 ,例如:1*2=1,3*2=2,则函数
,例如:1*2=1,3*2=2,则函数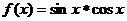 的值域为
的值域为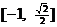 。
。
2、已知函数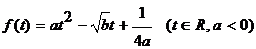 的最大值为正实数,集合
的最大值为正实数,集合
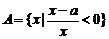 ,集合
,集合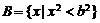 。
。
(1)求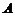 和
和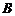 ;
;
(2)定义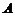 与
与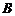 的差集:
的差集: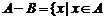 且
且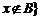 。
。
设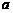 ,
,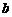 ,
,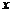 均为整数,且
均为整数,且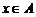 。
。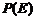 为
为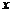 取自
取自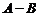 的概率,
的概率,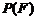 为
为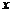 取自
取自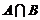 的概率,写出
的概率,写出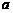 与
与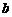 的二组值,使
的二组值,使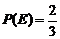 ,
,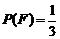 。
。
(3)若函数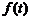 中,
中,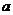 ,
,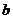 是(2)中
是(2)中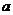 较大的一组,试写出
较大的一组,试写出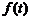 在区间[
在区间[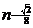 ,n]上的最大值函数
,n]上的最大值函数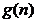 的表达式。
的表达式。
答案:(1)∵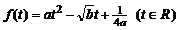 ,配方得
,配方得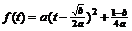 ,由
,由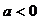 得最大值
得最大值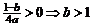 。……………………………………………………………3分
。……………………………………………………………3分
∴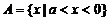 ,
,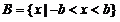 。…………………………6分
。…………………………6分
(2)要使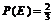 ,
,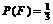 。可以使①
。可以使①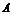 中有3个元素,
中有3个元素,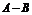 中有2个元素,
中有2个元素,
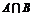 中有1个元素。则
中有1个元素。则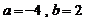 。…………………………………………………9分
。…………………………………………………9分
②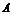 中有6个元素,
中有6个元素,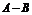 中有4个元素,
中有4个元素,
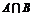 中有2个元素。则
中有2个元素。则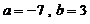 …………………………………………………………………………12分
…………………………………………………………………………12分
(3)由(2)知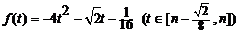 …………………………13分
…………………………13分
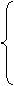
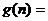
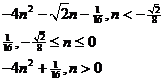 ………………………………………………18分
………………………………………………18分
1、已知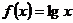
(1)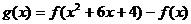 ,
求
,
求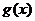 的最小值
的最小值
(2)P、Q关于点(1,2)对称,若点P在曲线C上移动时,点Q的轨迹是函数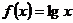 的图象,求曲线C的轨迹方程。
的图象,求曲线C的轨迹方程。
(3)在中学数学中,从特殊到一般,从具体到抽象是常见的一种思维形式。如从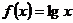 可抽象出
可抽象出 的性质,试分别写出一个具体的函数,抽象出下列相应的性质
的性质,试分别写出一个具体的函数,抽象出下列相应的性质
由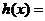 可抽象出
可抽象出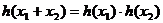
由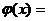 可抽象出
可抽象出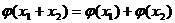
(1)
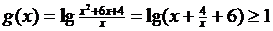 …………3’
…………3’
等号当x=2时成立,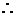
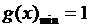 …………………………4’
…………………………4’
(2)设P(x,y)则Q(2-x,4-y)………………………………………………5’
由4-y=lg(2-x)可得:y=4-lg(2-x)………………………………8’
(3) h(x)=_______y=2x等_______, 9’ φ(x)=____y=lgx等__11’
15.已知数列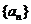 的前
的前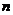 项和为
项和为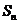 ,点
,点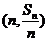 在直线
在直线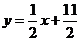 上;数列
上;数列 满足
满足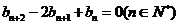 ,且
,且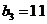 ,它的前9项和为153.
,它的前9项和为153.
(1)求数列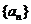 、
、 的通项公式;
的通项公式;
(2)设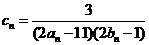 ,数列
,数列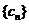 的前
的前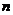 项和为
项和为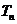 ,求使不等式
,求使不等式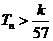 对一切
对一切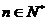 都成立的最大正整数
都成立的最大正整数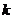 的值;
的值;
(3)设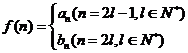 ,是否存在
,是否存在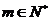 ,使得
,使得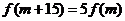 成立?若存在,求出
成立?若存在,求出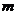 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
14、下列四个命题:
①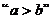 是
是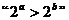 成立的充要条件;
成立的充要条件;
②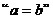 是“
是“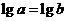 ”成立的充分不必要条件;
”成立的充分不必要条件;
③函数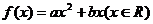 为奇函数的充要条件是
为奇函数的充要条件是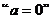
④定义在R上的函数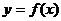 是偶函数的必要条件是
是偶函数的必要条件是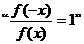 。
。
其中真命题的序号是 。(把真命题的序号都填上)
13、已知实数x,y满足条件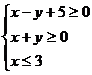 ,
,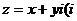 为虚数单位),则
为虚数单位),则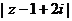 的最大值和最小值分别是 。
的最大值和最小值分别是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com