
20. (1)∵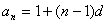 ,
,
∴ 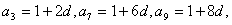 ………………………………4分
………………………………4分
于是 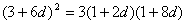 ,
,
注意到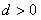 ,得
,得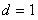 ,所以
,所以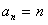 . ………………………………7分
. ………………………………7分
(2) 因为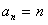 ,所以
,所以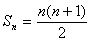 ,于是
,于是

当且仅当 ,即
,即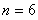 时,
时,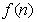 的最大值为
的最大值为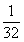 . ………………14分
. ………………14分
19、 (1)由已知,可得  ,
,
即  . ………………………………3分
. ………………………………3分
由正弦定理,得 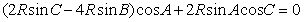 ,
,
∴ 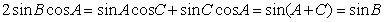 ,
,
由 ∴
∴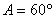 . ………………………………7分
. ………………………………7分
法二 由余弦定理,得  ,
,
∴ 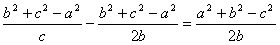 ,
,
∴ 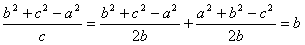 ,
,
∴ 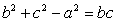 .于是由
.于是由 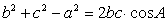 ,
,
得 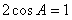 ,∴
,∴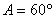 .
.
(2)由已知,得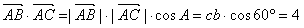 ,
,
∴ 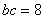 ………………………………10分
………………………………10分
∴ 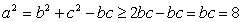 ,即
,即 的最小值为
的最小值为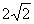 .
.
………………………………14分
18、解:
(1)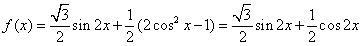
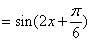

所以 函数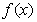 的周期是
的周期是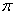 ,又由
,又由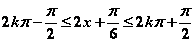 可得函数
可得函数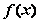 的
的
递增区间为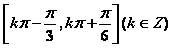 。。。。。。。。。。。。。8分
。。。。。。。。。。。。。8分
(2)将函数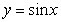 的图象向左平移
的图象向左平移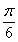 个单位,再将所得图象上每一点的横坐标变为原来的
个单位,再将所得图象上每一点的横坐标变为原来的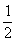 倍(纵坐标不变式),得函数
倍(纵坐标不变式),得函数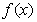 的图象。。。。。。。。。。。6分
的图象。。。。。。。。。。。6分
11、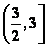 ;12、
;12、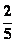 ;13、3;14、
;13、3;14、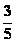 ;15、20;16、
;15、20;16、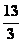 ;17、(1)(2)
;17、(1)(2)
CBCBC CC DBC
22.(本小题满分16分)
已知函数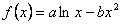 图象上一点P(2,f(2))处的切线方程为
图象上一点P(2,f(2))处的切线方程为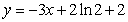 .
.
(Ⅰ)求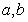 的值;
的值;
(Ⅱ)若方程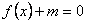 在
在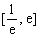 内有两个不等实根,求
内有两个不等实根,求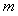 的取值范围;
的取值范围;
(Ⅲ)令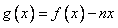 ,如果
,如果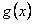 图象与
图象与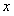 轴交于
轴交于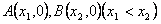 ,AB中点为
,AB中点为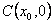 ,求证:
,求证: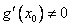 .
.
2010届余杭高级中学高三第二次月考数学试题(理科)
命题人:吴晓曙 校对人:曹凤山
21.(本题满分14分)
已知 若
若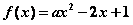 在
在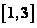 上的最大值为
上的最大值为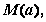 最小值为
最小值为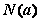 ,
,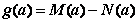
(1)求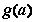 的函数表达式;
的函数表达式;
(2)判断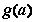 的单调性,并求出
的单调性,并求出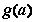 的最小值
的最小值
20. (本题满分14分)
已知数列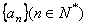 是首项为1的等差数列,其公差
是首项为1的等差数列,其公差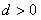 ,且
,且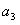 、
、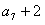 、
、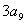 成等比数列.
(1)求数列
成等比数列.
(1)求数列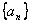 的通项公式;
的通项公式;
(2) 设数列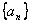 的前
的前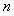 项和为
项和为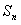 ,求
,求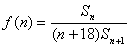 的最大值
的最大值
19. (本题满分14分)
在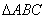 中,角A、B、C所对的边分别为
中,角A、B、C所对的边分别为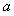 、
、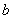 、
、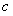 .已知向量
.已知向量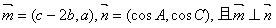 .
.
(1) 求角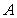 的大小;
(2) 若
的大小;
(2) 若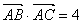 ,求边
,求边 的最小值.
的最小值.
18.(本题满分14分)
已知函数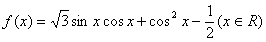
(1)求函数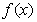 的周期和单调递增区间;
的周期和单调递增区间;
(2)函数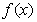 的图象可由函数
的图象可由函数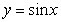 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com