
1.全称量词与存在量词
(1)全称量词:对应日常语言中的“一切”、“任意的”、“所有的”、“凡是”、“任给”、“对每一个”等词,用符号“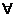 ”表示。
”表示。
(2)存在量词:对应日常语言中的“存在一个”、“至少有一个”、“有个”、“某个”、“有些”、“有的”等词,用符号“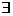 ”表示。
”表示。
4、四种命题:记“若q则p”为原命题,则否命题为“若非p则非q”,逆命题为“若q则p“,逆否命题为”若非q则非p“。其中互为逆否的两个命题同真假,即等价。因此,四种命题为真的个数只能是偶数个。
例6、(2008广东高考)命题“若函数 在其定义域内是减函数,则
在其定义域内是减函数,则 ”的逆否命题是( )
”的逆否命题是( )
A、若 ,则函数
,则函数 在其定义域内不是减函数
在其定义域内不是减函数
B、若 ,则函数
,则函数 在其定义域内不是减函数
在其定义域内不是减函数
C、若 ,则函数
,则函数 在其定义域内是减函数
在其定义域内是减函数
D、若 ,则函数
,则函数 在其定义域内是减函数
在其定义域内是减函数
解:逆否命题是将原命题的结论的否定作为条件,原命题的条件的否定作为结论,故应选(A)。
例7、已知命题 方程
方程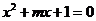 有两个不相等的负数根;
有两个不相等的负数根;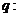 方程
方程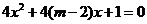 无实根.若“
无实根.若“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,求实数
”为假,求实数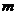 的取值范围.
的取值范围.
解: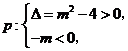
 .
.
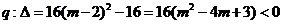 ,
,
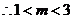 .
.
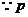 或
或 为真,
为真, 且
且 为假,
为假,
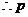 真,
真, 假或
假或 假,
假, 真.
真.
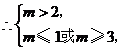 或
或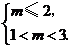 ,故
,故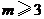 或
或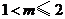 .
.
考点4、全称量词与存在量词
3、复合命题的真假:对p且q而言,当q、p为真时,其为真;当p、q中有一个为假时,其为假。对p或q而言,当p、q均为假时,其为假;当p、q中有一个为真时,其为真;当p为真时,非p为假;当p为假时,非p为真。
2、复合命题的形式:p且q,p或q,非p;
1、命题分类:真命题与假命题,简单命题与复合命题;
3、学会画Venn图,并会用Venn图来解决问题。
例3、设集合A={x|2x+1<3},B={x|-3<x<2},则A B等于(
)
B等于(
)
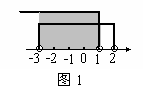 (A) {x|-3<x<1} (B)
{x|1<x<2}
(A) {x|-3<x<1} (B)
{x|1<x<2}
(C){x|x>-3} (D) {x|x<1}
解:集合A={x|2x+1<3}={x|x<1},集合A和集合B在数轴上表示如图1所示,A B是指集合A和集合B的公共部分,故选(A)。
B是指集合A和集合B的公共部分,故选(A)。
 例4、经统计知,某村有电话的家庭有35家,有农用三轮车的家庭有65家,既有电话又有农用三轮车的家庭有20家,则电话和农用三轮车至少有一种的家庭数为
( )
例4、经统计知,某村有电话的家庭有35家,有农用三轮车的家庭有65家,既有电话又有农用三轮车的家庭有20家,则电话和农用三轮车至少有一种的家庭数为
( )
A. 60 B. 70 C. 80 D. 90
解:画出Venn图,如图2,画图可得到有一种物品的家庭数为:15+20+45=80.故选(C)。
例5、(2008广东卷)第二十九届夏季奥林匹克运动会将于2008年8月8日在北京举行,若集合A={参加北京奥运会比赛的运动员},集合B={参加北京奥运会比赛的男运动员}。集合C={参加北京奥运会比赛的女运动员},则下列关系正确的是( )
A.A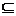 B
B.B
B
B.B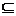 C
C.A∩B=C D.B∪C=A
C
C.A∩B=C D.B∪C=A
解:由题意可知,应选(D)。
考点3、逻辑联结词与四种命题
2、运算律,如A∩(B∪C)=(A∩B)∪(A∩C),CU(A∩B)=(CUA)∪(CUB),
CU(A∪B)=(CUA)∩(CUB)等。
1、交,并,补,定义:A∩B={x|x∈A且x∈B},A∪B={x|x∈A,或x∈B},CUA={x|x∈U,且x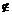 A},集合U表示全集;
A},集合U表示全集;
4、注意空集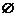 的特殊性,在解题中,若未能指明集合非空时,要考虑到空集的可能性,如A
的特殊性,在解题中,若未能指明集合非空时,要考虑到空集的可能性,如A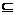 B,则有A=
B,则有A=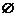 或A≠
或A≠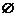 两种可能,此时应分类讨论
两种可能,此时应分类讨论
例1、下面四个命题正确的是
(A)10以内的质数集合是{1,3,5,7} (B)方程x2-4x+4=0的解集是{2,2}
(C)0与{0}表示同一个集合 (D)由1,2,3组成的集合可表示为{1,2,3}或{3,2,1}
解:选(D),最小的质数是2,不是1,故(A)错;由集合的定义可知(B)(C)都错。
例2、已知集合A=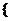 -1,3,2
-1,3,2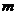 -1
-1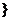 ,集合B=
,集合B=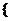 3,
3,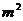
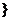 .若B
.若B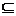 A,则实数
A,则实数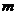 = .
= .
解:由B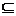 A,且
A,且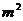 不可能等于-1,可知
不可能等于-1,可知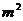 =2
=2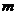 -1,解得:
-1,解得: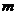 =1。
=1。
考点2、集合的运算
3、解答集合问题,首先要正确理解集合有关概念,特别是集合中元素的三要素;对于用描述法给出的集合{x|x∈P},要紧紧抓住竖线前面的代表元素x以及它所具有的性质P;要重视发挥图示法的作用,通过数形结合直观地解决问题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com