
6.平面
(1)对平面的理解
平面是一个不加定义、只须理解的最基本的原始概念.
立体几何中的平面是理想的、绝对平且无限延展的模型,平面是无大小、厚薄之分的.类似于我们以前学的直线,它可以无限延伸,它是不可度量的.
(2)对公理的剖析
(1)公理1的内容反映了直线与平面的位置关系,公理1的条件“线上不重合的两点在平面内”是公理的必要条件,结论是“线上所有点都在面内”.这个结论阐述了两个观点:一是整条直线在平面内;二是直线上所有点在平面内.
其作用是:可判定直线是否在平面内、点是否在平面内.
(2)公理2中的“有且只有一个”的含义要准确理解.这里的“有”是说图形存在,“只有一个”是说图形唯一,确定一个平面中的“确定”是“有且只有”的同义词,也是指存在性和唯一性这两方面.这个术语今后也会常常出现,要理解好.
其作用是:一是确定平面;二是证明点、线共面.
(3)公理3的内容反映了平面与平面的位置关系,它的条件简而言之是“两面共一点”,结论是“两面共一线,且过这一点,线唯一”.对于本公理应强调对于不重合的两个平面,只要它们有公共点,它们就是相交的位置关系,交集是一条直线.
其作用是:其一它是判定两个平面是否相交的依据,只要两个平面有一个公共点,就可以判定这两个平面必相交于过这点的一条直线;其二它可以判定点在直线上,点是两个平面的公共点,线是这两个平面的公共交线,则这点在交线上.
5、直观图画法
斜二测画法的规则:
(1)在空间图形中取互相垂直的x轴和y轴,两轴交于O点,再取z轴,使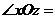 90°,且
90°,且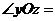 90°.
90°.
(2)画直观图时把它们画成对应的 轴、
轴、 轴和
轴和 轴,它们相交于
轴,它们相交于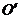 ,并使
,并使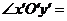 45°,
45°, 90°。
90°。
(3)已知图形中平行于x轴、y轴或z轴的线段,在直观图中分别画成平行于 轴、
轴、 轴和
轴和 轴的线段.
轴的线段.
(4)已知图形中平行于x轴和z轴的线段,在直观图中长度相等;平行于y轴的线段,长度取一半.
4、中心投影和平行投影
(1)中心投影:投射线均通过投影中心的投影。
(2)平行投影:投射线相互平行的投影。
(3)三视图的位置关系与投影规律
三视图的位置关系为:俯视图在主视图的下方、左视图在主视图的右方.
三视图之间的投影规律为:
主、俯视图---长对正;主、左视图---高平齐;俯、左视图---宽相等.
3、空间几何体的体积
(1)柱体(棱柱、圆柱)的体积等于它的底面积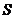 和高
和高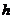 的积,即
的积,即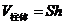 .其中底面半径是
.其中底面半径是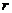 ,高是
,高是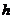 的圆柱的体积是
的圆柱的体积是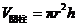 .
.
(2)如果一个锥体(棱锥、圆锥)的底面积是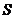 ,高是
,高是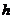 ,那么它的体积是
,那么它的体积是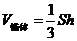 .其中底面半径是
.其中底面半径是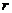 ,高是
,高是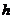 的圆锥的体积是
的圆锥的体积是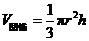 ,就是说,锥体的体积是与其同底等高柱体体积的
,就是说,锥体的体积是与其同底等高柱体体积的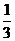 .
.
(3)如果台体(棱台、圆台)的上、下底面积分别是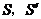 ,高是
,高是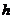 ,那么它的体积是
,那么它的体积是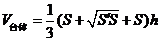 .其中上、下底半径分别是
.其中上、下底半径分别是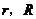 ,高是
,高是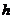 的圆台的体积是
的圆台的体积是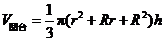 .
.
(4)球的体积公式: .
.
2、空间几何体的侧面积、表面积
(1)棱柱侧面展开图的面积就是棱柱的侧面积,棱柱的表面积就是它的侧面积与两底面面积的和.
因为直棱柱的各个侧面都是等高的矩形,所以它的展开图是以棱柱的底面周长与高分别为长和宽的矩形.如果设直棱柱底面周长为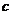 ,高为
,高为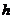 ,则侧面积
,则侧面积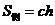 .
.
若长方体的长、宽、高分别是a、b、c,则其表面积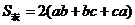 .
.
(2)圆柱的侧面展开图是一个矩形.矩形的宽是圆柱母线的长,矩形的长为圆柱底面周长.如果设圆柱母线的长为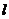 ,底面半径为r,那么圆柱的侧面积
,底面半径为r,那么圆柱的侧面积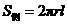 ,此时圆柱底面面积
,此时圆柱底面面积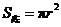 .所以圆柱的表面积
.所以圆柱的表面积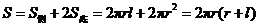 .
.
(3)圆锥的侧面展开图是以其母线为半径的扇形.如果设圆锥底面半径为r,母线长为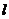 ,则侧面积
,则侧面积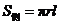 ,那么圆锥的表面积是由其侧面积与底面面积的和构成,即为
,那么圆锥的表面积是由其侧面积与底面面积的和构成,即为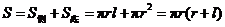 .
.
(4)正棱锥的侧面展开图是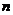 个全等的等腰三角形.如果正棱锥的周长为
个全等的等腰三角形.如果正棱锥的周长为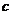 ,斜高为
,斜高为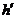 ,则它的侧面积
,则它的侧面积 .
.
(5)正棱台的侧面积就是它各个侧面积的和.如果设正棱台的上、下底面的周长是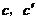 ,斜高是
,斜高是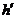 ,那么它的侧面积是
,那么它的侧面积是 .
.
(6)圆台侧面展开图是以截得该圆台的圆锥母线为大圆半径,圆锥与圆台的母线之差为小圆半径的一个扇环.如果设圆台的上、下底面半径分别为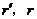 ,母线长为
,母线长为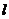 ,那么它的侧面积是
,那么它的侧面积是 .
.
圆台的表面积等于它的侧面积与上、下底面积的和,
即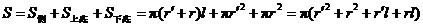 .
.
(7)球的表面积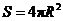 ,即球的表面积等于其大圆面积的四倍.
,即球的表面积等于其大圆面积的四倍.
1、空间几何体的结构特征
(1)棱柱、棱锥、棱台和多面体
棱柱是由满足下列三个条件的面围成的几何体:①有两个面互相平行;②其余各面都是四边形;③每相邻两个四边形的公共边都互相平行;棱柱按底面边数可分为:三棱柱、四棱柱、五棱柱等.棱柱性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等; ②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等多边形.
③过棱柱不相邻的两条侧棱的截面都是平行四边形.
棱锥是由一个底面是多边形,其余各面是有一个公共顶点的三角形所围成的几何体.棱锥具有以下性质:①底面是多边形;②侧面是以棱锥的顶点为公共点的三角形;③平行于底面的截面和底面是相似多边形,相似比等于从顶点到截面和从顶点到底面距离的比.截面面积和底面面积的比等于上述相似比的平方.
棱台是棱锥被平行于底面的一个平面所截后,截面和底面之间的部分.由棱台定义可知,所有侧棱的延长线交于一点,继而将棱台还原成棱锥.
多面体是由若干个多边形围成的几何体.多面体有几个面就称为几面体,如三棱锥是四面体.
(2)圆柱、圆锥、圆台、球
分别以矩形的一边,直角三角形的一直角边,直角梯形垂直于底边的腰所在的直线,半圆以它的直径所在直线为旋转轴,旋转一周而形成的几何体叫做圆柱、圆锥、圆台、球
圆柱、圆锥和圆台的性质主要有:①平行于底面的截面都是圆;②过轴的截面(轴截面)分别是全等的矩形、等腰三角形、等腰梯形;③圆台的上底变大到与下底相同时,可以得到圆柱;圆台的上底变小为一点时,可以得到圆锥.
9.以等差、等比数列的基本问题为主,突出数列与函数、数列与方程、数列与不等式、数列与几何等的综合应用.
以上关于数列二轮复习的几点建议仅供复习时参考,各校应根据自己的实际情况进行增减,四星以下的学校应重在基础,对于数列的综合问题可略讲,甚至不讲.
8.掌握一些数列求和的方法
(1)分解成特殊数列的和
(2)裂项求和
(3)“错位相减”法求和
7.根据递推关系,运用化归思想,将其转化为常见数列;
6.掌握数列通项an与前n项和Sn 之间的关系;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com