
2.向量的表示方法:①用有向线段表示;②用字母 、
、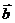 等表示;③平面向量的坐标表示:分别取与
等表示;③平面向量的坐标表示:分别取与 轴、
轴、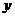 轴方向相同的两个单位向量
轴方向相同的两个单位向量 、
、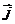 作为基底。任作一个向量
作为基底。任作一个向量 ,由平面向量基本定理知,有且只有一对实数
,由平面向量基本定理知,有且只有一对实数 、
、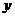 ,使得
,使得
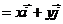 ,
, 叫做向量
叫做向量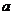 的(直角)坐标,记作
的(直角)坐标,记作 ,其中
,其中 叫做
叫做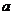 在
在 轴上的坐标,
轴上的坐标,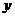 叫做
叫做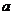 在
在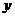 轴上的坐标, 特别地,
轴上的坐标, 特别地,
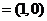 ,
,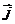
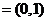 ,
, 。
。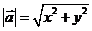 ;若
;若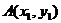 ,
, ,则
,则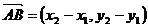 ,
,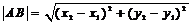
1.向量的概念:既有大小又有方向的量叫向量,有二个要素:大小、方向.
5.利用函数知识解应用题是高考重点,应引起重视.
4.含参数函数的讨论是函数问题中的难点及重点,复习时应适当加强这方面的训练,做到条理清楚、分类明确、不重不漏.
3.二次函数是初中、高中的结合点,应引起重视,复习时要适当加深加宽.二次函数与二次方程、二次不等式有着密切的联系,要沟通这些知识之间的内在联系,灵活运用它们去解决有关问题.
2.掌握函数图象的基本变换,如平移、翻转、对称等.
基本函数:一次函数、二次函数、指数函数与对数函数,它们的图象与性质是函数的基石,判断、证明与应用函数的三大特性(单调性、奇偶性、周期性)是高考命题的切入点,有单一考查,也有综合考查.函数的图象、图象的变换是高考热点,应用函数知识解其他问题,特别是解应用题能很好地考查学生分析问题、解决问题的能力,这类问题在高考中具有较强的生存力.配方法、待定系数法、数形结合法、分类讨论等,这些方法构成了函数这一章应用的广泛性、解法的多样性和思维的创造性,这均符合高考试题改革的发展趋势.
特别在“函数”这一章中,数形结合的思想比比皆是,深刻理解和灵活运用这一思想方法,不仅会给解题带来方便,而且这正是充分把握住了中学数学的精髓和灵魂的体现.
复习函数时要注意:
1.深刻理解一些基本函数,如二次函数、指数函数、对数函数的图象与性质,对数与形的基本关系能相互转化.
(二)2010年高考预测
1.考查有关函数单调性和奇偶性的试题,从试题上看,抽象函数和具体函数都有,有向抽象函数发展的趋势,另外试题注重对转化思想的考查,且都综合地考查单调性与奇偶性.
2.考查与函数图象有关的试题,要从图中(或列表中)读取各种信息,注意利用平移变换、伸缩变换、对称变换,注意函数的对称性、函数值的变化趋势,培养运用数形结合思想来解题的能力.
3.考查与指数函数和对数函数有关的试题.对指数函数与对数函数的考查,大多以基本函数的性质为依托,结合运算推理来解决.
4加强函数思想、转化思想的考查是高考的一个重点.善于转化命题,引进变量建立函数,运用变化的方法、观点解决数学试题以提高数学意识,发展能力.
5、注意与导数结合考查函数的性质.
6、函数的应用,是与实际生活结合的试题,应加强重视。
(一)思想方法总结
1. 数形结合
2. 分类讨论
3. 函数与方程
(一) 函数性质法
函数的特征是通过其性质(如奇偶性,单调性周期性,特殊点等)反应出来的,抽象函数也是如此,只有充分挖掘和利用题设条件和隐含的性质,灵活进行等价转化,抽象函数问题才能转化,化难为易,常用的解题方法有:1,利用奇偶性整体思考;2,利用单调性等价转化;3,利用周期性回归已知4;利用对称性数形结合;5,借助特殊点,布列方程等.
(二 )特殊化方法
1、在求解函数解析式或研究函数性质时,一般用代换的方法,将x换成-x等
2、在求函数值时,可用特殊值代入
3、研究抽象函数的具体模型,用具体模型解选择题,填空题,或由具体模型函数对综合题,的解答提供思路和方法.
总之,抽象函数问题求解,用常规方法一般很难凑效,但我们如果能通过对题目的信息分析与研究,采用特殊的方法和手段求解,往往会收到事半功倍之功效,真有些山穷水复疑无路,柳暗花明又一村的快感.
例13、(2008陕西文) 定义在 上的函数
上的函数 满足
满足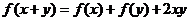 (
(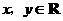 ),
), ,则
,则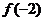 等于( )
等于( )
A.2 B.3 C.6 D.9
解:令 ,令
,令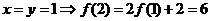 ;
;
令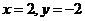 得
得
考点六:函数的综合应用
函数的综合运用主要是指运用函数的知识、思想和方法综合解决问题.函数描述了自然界中量的依存关系,是对问题本身的数量本质特征和制约关系的一种刻画,用联系和变化的观点提出数学对象,抽象其数学特征,建立函数关系.因此,运动变化、相互联系、相互制约是函数思想的精髓,掌握有关函数知识是运用函数思想的前提,提高用初等数学思想方法研究函数的能力,树立运用函数思想解决有关数学问题的意识是运用函数思想的关键.
例14、(2008广东高考试题)某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层、每层2000平方米的楼房。经测算,如果将楼房建为x(x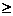 10)层,则每平方米的 平均建筑费用为560+48x(单位:元)。为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
10)层,则每平方米的 平均建筑费用为560+48x(单位:元)。为了使楼房每平方米的平均综合费用最少,该楼房应建为多少层?
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= )
)
[解析]:设楼房每平方米的平均综合费为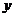 元,依题意得
元,依题意得

则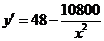 ,令
,令 ,即
,即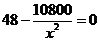 ,解得
,解得
当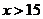 时,
时,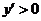 ;当
;当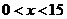 时,
时,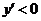 ,
,
因此,当 时,
时,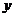 取得最小值,
取得最小值,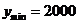 元.
元.
答:为了使楼房每平方米的平均综合费最少,该楼房应建为15层。
[点评]:这是一题应用题,利用函数与导数的知识来解决问题。利用导数,求函数的单调性、求函数值域或最值是一种常用的方法.
例15、(2007湖北文科高考试题)某商品每件成本9元,售价为30元,每星期卖出432件. 如果降低价格,销售量可以增加,
且每星期多卖出的商品件数与商品单价的降低值 (单位:元,
(单位:元,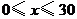 )的平方成正比.
)的平方成正比.
已知商品单价降低2元时,一星期多卖出24件.
(I)将一个星期的商品销售利润表示成 的函数;
的函数;
(II)如何定价才能使一个星期的商品销售利润最大?
本小题主要考查根据实际问题建立数学模型,以及运用函数、导数的知识解决实际问题的能力.
[解析]:(Ⅰ)设商品降价 元,则多卖的商品数为
元,则多卖的商品数为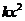 ,若记商品在一个星期的获利为
,若记商品在一个星期的获利为 ,
,
则依题意有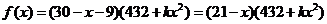 ,
,
又由已知条件, ,于是有
,于是有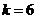 ,
,
所以 .
.
(Ⅱ)根据(Ⅰ),我们有 .
.
 |
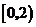 |
2 |
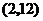 |
12 |
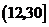 |
 |
 |
0 |
 |
0 |
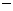 |
 |
 |
极小 |
 |
极大 |
 |
故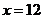 时,
时, 达到极大值.因为
达到极大值.因为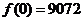 ,
,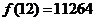 ,
,
所以定价为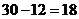 元能使一个星期的商品销售利润最大.
元能使一个星期的商品销售利润最大.
[点评]:本小题主要考查根据实际问题建立数学模型,以及运用函数、导数的知识解决实际问题的能力.
考点七、函数的零点
例16、(2008山东荷泽模拟题)函数 的零点所在的区间是 )
的零点所在的区间是 )
A.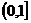 B.(1,10) C.
B.(1,10) C. D.
D.
解:因为f(1)=0-1<0,f(10)=1-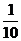 >0,即f(1)•f(10)<0,
>0,即f(1)•f(10)<0,
所以函数f(x)在区间(1,10)之间有零点。
[点评]:如果函数f(x)在区间[a,b]上连续,且f(a)•f(b)<0,则函数f(x)在区间(a,b)上有零点,函数的零点,二分法,函数的应用都是函数的重点内容。
例17、(2007广东高考题)已知a是实数,函数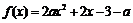 ,如果函数
,如果函数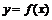 在区间[-1,1]上有零点,
在区间[-1,1]上有零点,
求实数a的取值范围。
[解析]当a=0时,函数为f (x)=2x
-3,其零点x= 不在区间[-1,1]上。
不在区间[-1,1]上。
当a≠0时,函数f (x) 在区间[-1,1]分为两种情况:
①函数在区间[─1,1]上只有一个零点,此时
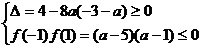
或
解得1≤a≤5或a=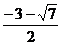
②函数在区间[─1,1]上有两个零点,此时
 或
或
解得a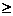 5或a<
5或a<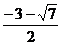
综上所述,如果函数在区间[─1,1]上有零点,那么实数a的取值范围为
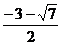
(-∞, ]∪[1, +∞)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com