
12.点P分有向线段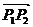 所成的比的
所成的比的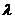 :
: 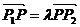 ,P内分线段
,P内分线段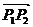 时,
时, 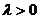 ; P外分线段
; P外分线段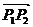 时,
时, 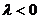 .
定比分点坐标公式、中点坐标公式、三角形重心公式:
.
定比分点坐标公式、中点坐标公式、三角形重心公式:
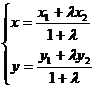
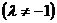 、
、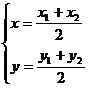 、
、 
11.两向量平行、垂直的充要条件 设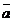 =(
=(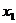 ,
,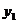 ),
), 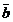 =(
=(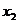 ,
,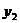 )
)
①a⊥b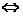 a·b=0 ,
a·b=0 ,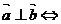
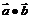 =
=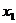
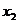 +
+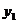
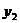 =0;
=0;
②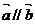 (
( ≠
≠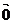 )充要条件是:有且只有一个非零实数λ,使
)充要条件是:有且只有一个非零实数λ,使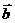 =λ
=λ 。
。

向量的平行与垂直的坐标运算注意区别,在解题时容易混淆。
10.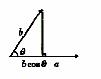 向量
向量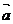 和
和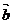 的数量积:①
的数量积:①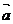 ·
·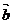 =|
=| 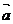 |·|
|·|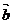 |cos
|cos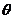 ,其中
,其中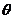 ∈[0,π]为
∈[0,π]为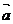 和
和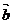 的夹角。②|
的夹角。②|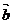 |cos
|cos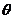 称为
称为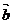 在
在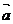 的方向上的投影。③
的方向上的投影。③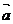 ·
·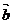 的几何意义是:
的几何意义是: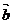 的长度|
的长度|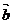 |在
|在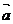 的方向上的投影的乘积,是一个实数(可正、可负、也可是零),而不是向量。
的方向上的投影的乘积,是一个实数(可正、可负、也可是零),而不是向量。
④若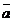 =(
=(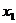 ,
,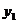 ),
), 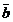 =(x2,
=(x2,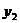 ), 则
), 则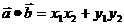
⑤运算律:a· b=b·a, (λa)· b=a·(λb)=λ(a·b), (a+b)·c=a·c+b·c。
⑥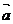 和
和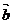 的夹角公式:cos
的夹角公式:cos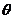 =
=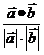 =
=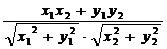
⑦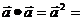 |
|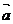 |2=x2+y2,或|
|2=x2+y2,或|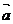 |=
|=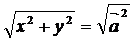 ⑧| a·b |≤| a |·| b |。
⑧| a·b |≤| a |·| b |。
9.平面向量基本定理:如果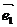 ,
,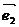 是同一平面内的两个不共线向量,那么对于这一平面内的任一向量
是同一平面内的两个不共线向量,那么对于这一平面内的任一向量 ,有且只有一对实数λ1,λ2使
,有且只有一对实数λ1,λ2使 =λ1
=λ1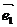 +λ2
+λ2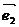 。(1)不共线向量
。(1)不共线向量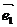 、
、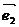 叫做表示这一平面内所有向量的一组基底;(2)基底不惟一,关键是不共线;(3)由定理可将任一向量
叫做表示这一平面内所有向量的一组基底;(2)基底不惟一,关键是不共线;(3)由定理可将任一向量 在给出基底
在给出基底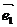 、
、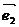 的条件下进行分解;(4)基底给定时,分解形式惟一. λ1,λ2是被
的条件下进行分解;(4)基底给定时,分解形式惟一. λ1,λ2是被 ,
,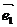 ,
,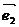 唯一确定的数量。
唯一确定的数量。
8. 向量共线定理 向量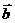 与非零向量
与非零向量 共线(也是平行)的充要条件是:有且只有一个非零实数λ,使
共线(也是平行)的充要条件是:有且只有一个非零实数λ,使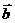 =λ
=λ 。
。
7.实数与向量的积:实数λ与向量 的积是一个向量,记作:λ
的积是一个向量,记作:λ
(1)|λ |=|λ||
|=|λ|| |;(2)λ>0时λ
|;(2)λ>0时λ 与
与 方向相同;λ<0时λ
方向相同;λ<0时λ 与
与 方向相反;λ=0时λ
方向相反;λ=0时λ =
=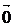 ;(3)运算定律 λ(μ
;(3)运算定律 λ(μ )=(λμ)
)=(λμ) ,(λ+μ)
,(λ+μ) =λ
=λ +μ
+μ ,λ(
,λ( +
+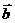 )=λ
)=λ +λ
+λ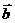
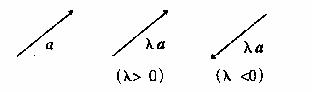
6.向量的加法、减法:
①求两个向量和的运算,叫做向量的加法。向量加法的三角形法则和平行四边形法则。②向量的减法向量 加上的
加上的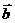 相反向量,叫做
相反向量,叫做 与
与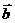 的差。即:
的差。即: -
-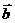 =
=  +
(-
+
(-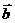 );
);
差向量的意义: 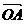 =
=  ,
, 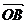 =
=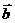 ,
则
,
则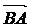 =
= -
- 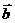

③平面向量的坐标运算:若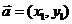 ,
,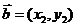 ,则
,则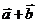
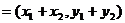 ,
,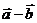
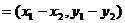 ,
,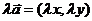 。
。
④向量加法的交换律: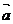 +
+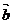 =
=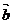 +
+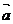 ;向量加法的结合律:(
;向量加法的结合律:(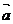 +
+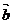 )
+
)
+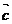 =
=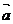 +
(
+
(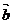 +
+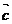 )
)
5.相等向量:长度相等且方向相同的向量叫相等向量.
4.平行向量:①方向相同或相反的非零向量叫平行向量;②我们规定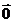 与任一向量平行.向量
与任一向量平行.向量 、
、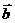 、
、 平行,记作
平行,记作 ∥
∥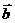 ∥
∥ .共线向量与平行向量关系:平行向量就是共线向量.
.共线向量与平行向量关系:平行向量就是共线向量.
3.零向量、单位向量:①长度为0的向量叫零向量,记为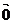 ;
②长度为1个单位长度的向量,叫单位向量.(注:
;
②长度为1个单位长度的向量,叫单位向量.(注: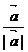 就是单位向量)
就是单位向量)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com