(二)新课讲解

　　 1.切线判定定理的导出

　　 上节课讲了“圆心到一条直线的距离等于该圆的半径，则该直线就是一条切线”.下面请同学们按我口述的上不骤作图(一同学到黑板上作)：

　　 先画⊙O，在⊙O上任取一点A，边结OA，过A点作⊙O的切线L.

　　 请学生回顾作图过程，切线L是如何作出来的？它满足哪些条件？

　　 引导学生总结出：①经过关径外端，②垂直于这条半径.

　　 如果一条直线满足以上两个条件，它就是一条切线，这就是本节要讲的“切线的判定定理”.(板书定理)

　　 切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线.

　　 请同学们思考一下，该判定定理的两个条件缺少一个可以吗？

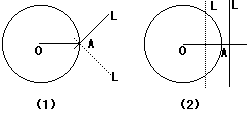　　 下图中L是不是圆的切线？(用教具演示下面两个反例)

　　 图(1)中直线L经过半径外端，但不与半径垂直.

　　 图(2)中直线L与半径垂直，但不经过径外端.

　　 从以上两个反例可看出，只满足其中一个条件的直线不是圆的切线.

　　 接着提出问题：若把定理中的“半径”改为“直径”可以吗？答案是肯定的.

　　 然后引导学生分析，切线的判定定理是由前一节所讲的“圆心到直线的距离等于半径时直线与圆相切”直接得到的，只是为了便于应用才把它改写成“经过半径外端并且垂直于这条半径的直线是圆的切线”这种形式，所以定理不再需要另加证明.

　　 提问：判定一条直线是圆的切线，我们有多少种方法呢？

　　 经过学生讨论后，师生小结以下三种方法(板书)：

　　 ①与圆有唯一公共点的直线是圆的切线.

　　 ②与圆心的距离等于半径的直线是圆的切线.

　　 ③经过半径外端并且垂直于这条半径的直线是圆的切线.

　　　 2.应用举例

　　 例1：已知：直线AB经过⊙O上的点C，并且OA=OB，CA=CB.

　　　　 已知：直线AB是⊙O的切线.

　 分析：已知直线AB和⊙O有一个公共点C，　

　 要证AB是⊙O的切线，只需连结这个公共点　　　

　 C和圆心O，得到半径OC，再证这条半径和直　

　 线AB垂直即可.

证明：连结OC　　　　　　　　　　　　

　∵OA=OB，CA=CB

　　 ∴OC是等腰三角形OAB底边AB上的中线　　　 ∴AB⊥OC

　　 直线AB经过半径OC的外端C，并且垂直于半径OC，所以AB是⊙O的切线.

　　 例2：已知：⊙O的直径长6cm，OA=OB=5cm，AB=8cm.

　　 求证：AB与⊙O相切.　

　 分析：题目中不明确直线和圆有公共点，故证

　 明相切，宣用方法2，因此只要证点O到直线AB　

　 的距离等于半径即可，从而想到作辅助线OC⊥　

　 AB于C.

　　 证明：过O点作OC⊥AB于C

　　 ∵OA=OB=5cm，AB=8cm

　　 ∴AC=BC=4cm

　　 ∴OC===3cm.

　　 又∵⊙O的直径长6cm

　　 ∴圆心O到直线AB的距离OC等于半径等于3cm.

　　 ∴AB与⊙O相切.

　　 让学生根据以上例题总结一下，证明直线与圆相切时，作辅助线的一般规律，以及证明方法的一般规律.

　　 经学生讨论后得出：

　　 ①已明确直线和圆有公共点，辅助线的作法是连结圆心和公共点，即得“半径”，再证“直线与半径垂直”.

　　 ②不明确直线和圆有公共点，辅助线的作法是过圆心作直线的垂线，再证“圆心到直线的距离等于半径”.

　　 注意：当题目中不明确直线和圆有公共点时，不能将圆上任意一点当作公共点而连结出半径.

　　 3.课堂练习：

　　 4.课堂小结：

　　 5.布置作业：

(一)复习引入

　　 回答下列问题：(投影显示)

　　 1.直线和圆有哪三种位置关系？这三种位置关系是如何定义？如何判定的？

　　 2.什么叫做圆的切线？根据这个定义我们可以怎样来判定一条直线是不是一个圆的切线？

　　 (要求学生举手回答，教师用教具演示)

　　 我们可以用切线的定义来判定一条直线是不是一个圆的切线，但有时使用起来很不方便，为此，我们还要学习切线的判定定理.

2.难点：圆的切线证明问题中，辅助线的添加方法.

1.重点：切线的判定定理.

3.情感目的：

　　 通过直观教具的演示和指导学生动手操作的过程，激发学生学习几何的积极性.

2.能力目的：

　　 (1)培养学生动手操作能力.

　　 (2)培养学生观察、探索、分析、总结、推理论证等能力.

1.知识目的：

　　 (1)掌握切线的判定定理.

　　 (2)应用切线的判定定理证明直线是圆的切线，初步掌握圆的切线证明问题中辅助线的添加方法.