
22. (本小题满分12分)(理科)设函数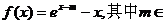 R.
R.
(I)求函数 的最值;
的最值;
(II)给出定理:如果函数 在区间[
在区间[ ]上连续,并且有
]上连续,并且有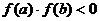 ,那么,函数
,那么,函数 在区间
在区间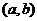 内有零点,即存在
内有零点,即存在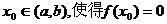 .
.
运用上述定理判断,当 时,函数
时,函数 在区间
在区间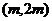 内是否存在零点.
内是否存在零点.
答案:(I)∵ ,
,
令 ……………………3分
……………………3分
|
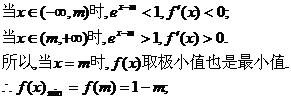
由(*)知f(x)无最大值. ……………………6分
(II)函数f(x)在[m,2m]上连续,
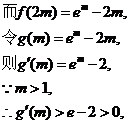
∴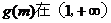 上递增. ……………………8分
上递增. ……………………8分
由 ……………………10分
……………………10分
又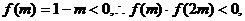
根据定理,可判断函数f(x)在区间(m,2m)上存在零点. …………12分
(文科)已知函数 (a、b∈R).
(a、b∈R).
(I)若函数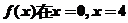 处取得极值,且极小值为-1,
处取得极值,且极小值为-1,
求f(x)的解析式;
(II)若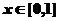 ,函数
,函数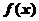 图象上的任意一点的切线斜率为k,当k≥-1恒成立时,求实数a的取值范围.
图象上的任意一点的切线斜率为k,当k≥-1恒成立时,求实数a的取值范围.
答案:(I)由 得
得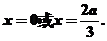
∴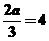 得a=6. ……………………………………3分
得a=6. ……………………………………3分
当x<0,
故当 达到极小值
达到极小值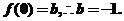
∴f(x)=-x3+6x2-1…………6分
(II)当 恒成立,
恒成立,
即令 对一切
对一切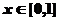 恒成立, …………9分
恒成立, …………9分
只需
所以,实数a的取值范围为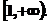 ………………………………12分
………………………………12分
21. (本小题满分12分)已知椭圆  的焦点在
的焦点在 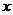 轴上,一个顶点的坐标是
轴上,一个顶点的坐标是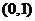 ,离心率等于
,离心率等于  .
.
(Ⅰ)求椭圆
 的方程;
的方程;
(Ⅱ)过椭圆  的右焦点
的右焦点 作直线
作直线 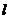 交椭圆
交椭圆  于
于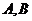 两点,交
两点,交  轴于
轴于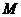 点,若
点,若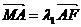 ,
, ,求证:
,求证: 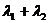 为定值.
为定值.
答案:(Ⅰ)设椭圆
 的方程为
的方程为 ,则由题意知
,则由题意知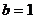 .
.
∴ 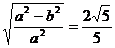 .即
.即 .∴
.∴  .
.
∴ 椭圆  的方程为
的方程为 . ---------------5分
. ---------------5分
(Ⅱ)方法一:设 点的坐标分别为
点的坐标分别为 ,
,
又易知 点的坐标为
点的坐标为 .
.
∵ 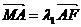 ,∴
,∴ .
.
∴  ,
, .
----------------7分
.
----------------7分
将 点坐标代入到椭圆方程中得:
点坐标代入到椭圆方程中得: ,
,
去分母整理,得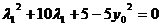 . ---------------10分
. ---------------10分
同理,由 可得:
可得: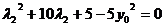 .
.
∴  ,
,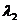 是方程
是方程 的两个根,
的两个根,
∴  . -----------------12分
. -----------------12分
方法二:设 点的坐标分别为
点的坐标分别为 ,又易知
,又易知 点的坐标为
点的坐标为 .
.
显然直线 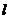 存在斜率,设直线
存在斜率,设直线 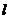 的斜率为
的斜率为 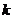 ,则直线
,则直线 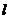 的方程是
的方程是 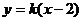 .
.
将直线 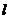 的方程代入到椭圆
的方程代入到椭圆  的方程中,消去
的方程中,消去  并整理得
并整理得
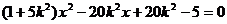 . ------------8分
. ------------8分
∴ 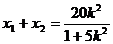 ,
, .
.
又 ∵ 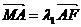 ,
, ,
,
将各点坐标代入得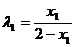 ,
,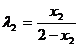 .---------10分
.---------10分
 .------12分
.------12分
20. (本小题满分12分)(理科)在等比数列{an}中,首项为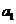 ,公比为
,公比为 ,
,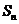 表示其前n项和.
表示其前n项和.
(I)记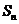 =A,
=A, = B,
= B,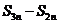 = C,证明A,B,C成等比数列;
= C,证明A,B,C成等比数列;
(II)若 ,
,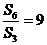 ,记数列
,记数列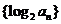 的前n项和为
的前n项和为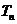 ,当n取何值时,
,当n取何值时,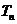 有最小值.
有最小值.
答案:(I)当 时,
时, ,
,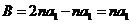 ,
, ,可见A,B,C成等比数列;
----2分
,可见A,B,C成等比数列;
----2分
当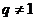 时,
时, ,
, ,
,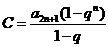 .
.
故有 ,
, .可得
.可得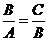 ,这说明A,B,C成等比数列.
,这说明A,B,C成等比数列.
综上,A,B,C成等比数列. ----6分
(II)若 ,则
,则 ,与题设矛盾,此情况不存在;
,与题设矛盾,此情况不存在;
若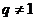 ,则
,则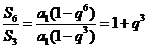 ,故有
,故有 ,解得
,解得 . --8分
. --8分
所以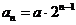 ,可知
,可知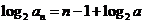 .所以数列
.所以数列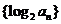 是以
是以 为首项,1为公差的等差数列.
为首项,1为公差的等差数列.
令 ,即
,即 .
.
因为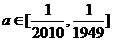 ,所以
,所以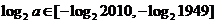 , ----10分
, ----10分
即得 ,
,
可知满足 的最大的n值为11.
的最大的n值为11.
所以,数列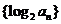 的前11项均为负值,从第12项开始都是正数.因此,当
的前11项均为负值,从第12项开始都是正数.因此,当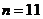 时,
时,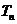 有最小值. ----12分
有最小值. ----12分
(文科)已知数列 的首项为1,前
的首项为1,前 项和为
项和为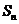 ,且满足
,且满足 ,
,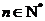 .数列
.数列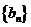 满足
满足 .
.
(I) 求数列 的通项公式;
的通项公式;
(II) 当 时,试比较
时,试比较 与
与 的大小,并说明理由.
的大小,并说明理由.
答案:(I) 由 … (1) , 得
… (1) , 得 … (2),
… (2),
由 (2)-(1) 得  , 整理,得
, 整理,得
 ,
,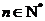 .
.
所以,数列 ,
,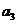 ,
,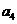 ,…,
,…,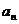 ,…是以4为公比的等比数列.
,…是以4为公比的等比数列.
其中,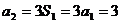 ,
,
所以 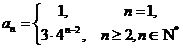 .
.
(II)由题意,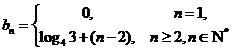 .
.
当 时,
时,
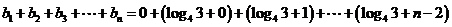

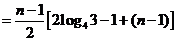
 ,
,
所以 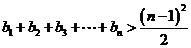 .
.
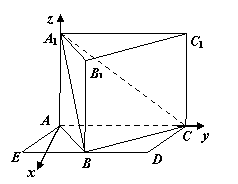
19.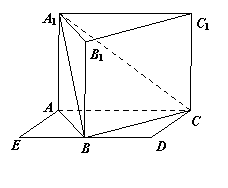 (本小题满分12分)如图,侧棱垂直底面的三棱柱
(本小题满分12分)如图,侧棱垂直底面的三棱柱 的
的
底面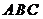 位于平行四边形
位于平行四边形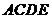 中,
中, ,
,
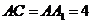 ,
, ,点
,点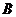 为
为 中点.
中点.
(Ⅰ)求证:平面 平面
平面 .
.
(Ⅱ)设二面角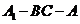 的大小为
的大小为 ,直线
,直线
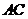 与平面
与平面 所成的角为
所成的角为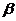 ,求
,求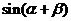 的值.
的值.
答案:(Ⅰ)法一、在平行四边形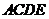 中, ∵
中, ∵ ,
, ,
, ,点
,点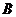 为
为 中点.
中点.
∴ ,
,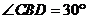 ,从而
,从而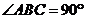 ,即
,即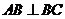 .----------3分
.----------3分
又 面
面 ,
, 面
面
∴ ,而
,而 , ∴
, ∴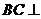 平面
平面 .
.
 ∵
∵ 平面
平面 ∴平面
∴平面 平面
平面 .----------6分
.----------6分
法二、∵ ,
, ,
, ,点
,点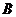 为
为 中点.
中点.
∴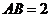 ,
, ,
,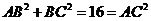 ,
,
∴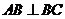 . ----------3分
. ----------3分
又 面
面 ,
, 面
面 ,∴
,∴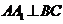 ,
,
而 ,∴
,∴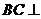 平面
平面
∵ 平面
平面 ,
,
∴平面 平面
平面 . ----------6分
. ----------6分
(Ⅱ)方法一、由(Ⅰ)可知 ,
,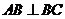
∴ 为二面角
为二面角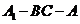 的平面角,即
的平面角,即
 ,
,
在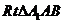 中,
中, ,
,
 ,
,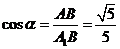 .----------8分
.----------8分
以 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系 如图所示,
如图所示,
其中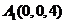 ,
, ,
, ,
, ,
,
 ,
, ,
,
设 为平面
为平面 的一个法向量,则
的一个法向量,则
 ,∴
,∴ 即
即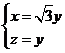 ----------10分
----------10分
令 ,得平面
,得平面 的一个法向量
的一个法向量 ,
,
则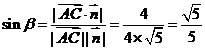 ,
,
又 , ∴
, ∴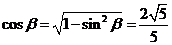 ,
,
 ∴
∴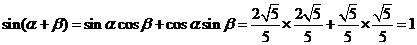 ,
,
即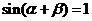 . ----------12分
. ----------12分
方法二、由(Ⅰ)可知 ,
,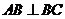
∴ 为二面角
为二面角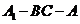 的平面角,即
的平面角,即
 ,
,
在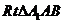 中,
中, ,
,
 ,
,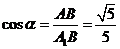 .
.
----------8分
过点 在平面
在平面 内作
内作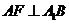 于
于 ,连结
,连结 ,
,
则由平面 平面
平面 ,且平面
,且平面 平面
平面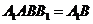 ,得
,得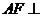 平面
平面
∴ 为直线
为直线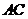 与平面
与平面 所成的角,即
所成的角,即 . ----------10分
. ----------10分
在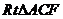 中,
中, ,
,
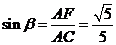 ,
,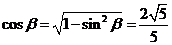 .
.
∴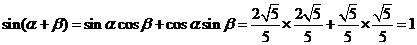 ,
,
即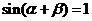 . ----------12分
. ----------12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com