
2.给出下列四个命题: ( )
①若集合 满足
满足 则
则 ;
;
②给定命题 , 若“
, 若“ ”为真,则“
”为真,则“ ”为真;
”为真;
③设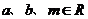 ,若
,若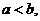 则
则 ;
;
④若直线 与直线
与直线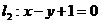 垂直,则
垂直,则 .
.
其中正确命题的个数是
A.1 B.2 C.3 D.4
1.若复数z满足 则z对应的点位于 ( )
则z对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
22.(本小题满分14分)
已知二次函数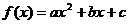 的图象的顶点坐标是
的图象的顶点坐标是
(Ⅰ)求 的表达式,并求出f(1)、f(2)的值;
的表达式,并求出f(1)、f(2)的值;
(Ⅱ)数列{an},{bn},若对任意的实数x都满足 ,
,
其中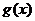 是定义在实数R上的一个函数,求数列{an},{bn}的通项公式;
是定义在实数R上的一个函数,求数列{an},{bn}的通项公式;
(Ⅲ)设圆 ,若圆Cn与圆Cn+1外切,{rn}是各项都是正
,若圆Cn与圆Cn+1外切,{rn}是各项都是正
数的等比数列,记Sn是前n个圆的面积之和,求 .
.
云南师范大学附中2010届高三数学模拟仿真试题(二)
21.(本小题满分12分)
某农产品去年各季度的市场价格如下表:
|
季 度 |
第一季度 |
第二季度 |
第三季度 |
第四季度 |
|
每吨售价 (单位:元) |
195.5 |
200.5 |
204.5 |
199.5 |
今年某公司计划按去年各季度市场价格的“平衡价m”(平衡价m是这样的一个量:与上年各季度售价差比较,m与各季度售价差的平方和最小)收购该种农产品,并按每100元纳税10元(又称征税率为10个百分点),计划可收购a万吨,政府为了鼓励收购公司多收购这种农产品,决定将税率降低x个百分点,预测收购量可增加2x个百分点.
(Ⅰ)根据题中条件填空,m= (元/吨)
(Ⅱ)写出税收y(万元)与x的函数关系式;
(Ⅲ)若要使此项税收在税率调节后不少于原计划税收的83.2%,试确定x的取值范围.
20.(本小题满分12分)
已知抛物线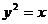 的弦AB与直线
的弦AB与直线 有公共点,且弦AB的中点N到y轴的距离为
有公共点,且弦AB的中点N到y轴的距离为
1,求弦AB长度的最大值,并求此时直线AB所在的直线的方程.

19.(本小题满分12分)
矩形ABCD中,AB=6,BC=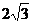 ,沿对角线BD将三角形ABD向上折起,使点A移至点P,使点P在平面BCD上的射影O在DC上,(如图).
,沿对角线BD将三角形ABD向上折起,使点A移至点P,使点P在平面BCD上的射影O在DC上,(如图).
 (Ⅰ)求证:PD⊥PC;
(Ⅰ)求证:PD⊥PC;
(Ⅱ)(理科)求二面角P-DB-C的大小;
(文科)求二面角P-DB-C的余弦值;
(Ⅲ)求直线CD与平面PBD所成角的大小.

18.(本小题满分12分)
已知△ABC中,A、B、C分别是三个内角,a、b、c分别是角A、B、C的对边,已知 的外接圆的半径为
的外接圆的半径为 .
.
(Ⅰ)求角C (Ⅱ)求△ABC面积S的最大值.
17.(本小题满分12分)
若 ,解关于x的不等式
,解关于x的不等式 .
.
16.对于函数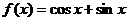 ,给出下列四个命题:
,给出下列四个命题:
①存在 ;
;
②存在 恒成立;
恒成立;
③存在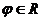 ,使函数
,使函数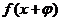 的图像关于y轴对称;
的图像关于y轴对称;
④函数 的图象关于点
的图象关于点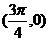 对称;
对称;
其中正确命题的序号是
15. 的值为
的值为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com