
1.已知集合 为实数集,集合
为实数集,集合 则
则 等于
等于
( )
A.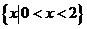 B.
B.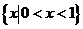 C.
C. D.
D.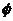
22.(本小题满分12分)
已知椭圆C的中心在坐标原点,离心率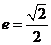 ,且其中一个焦点与抛物线
,且其中一个焦点与抛物线
的焦点重合.
(1)求椭圆C的方程;
(2)过点S(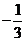 ,0)的动直线
,0)的动直线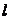 交椭圆C于A.B两点,试问:在坐标平面上是否存在一个定点T,使得无论
交椭圆C于A.B两点,试问:在坐标平面上是否存在一个定点T,使得无论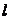 如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
如何转动,以AB为直径的圆恒过点T,若存在,求出点T的坐标;若不存在,请说明理由.
21.(本小题满分12分)
已知
(1)如果函数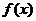 的单调递减区间为
的单调递减区间为 ,求函数
,求函数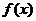 的解析式;
的解析式;
(2)若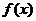 的导函数
的导函数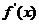 ,对任意的
,对任意的 ,不等式
,不等式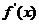 ≥
≥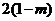 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
20.(本小题满分12分)
数列 中,
中,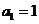 ,且
,且 ,数列
,数列 是等差数列,其公差
是等差数列,其公差 且
且 成等比数列.
成等比数列.
(1)求数列 .
. 的通项公式;
的通项公式;
(2)设数列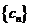 满足
满足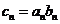 ,求
,求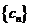 的前
的前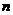 项和
项和 .
.
19.(本小题满分12分)
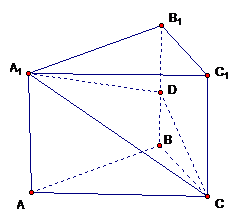
如图,在直三棱柱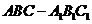 中,底面
中,底面 为等腰直角三角形,
为等腰直角三角形,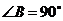 ,
,
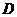 为棱
为棱 上一点,且面
上一点,且面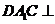 面
面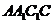 .
.
(1)求证: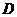 点为棱
点为棱 的中点;
的中点;
(2)若二面角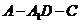 的平面角为
的平面角为 ,求
,求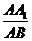 的值.
的值.
18.(本小题满分12分)
为迎接2010年上海世界博览会的召开,上海某高校对本校报名参加志愿者服务的学生进行英语.日语口语培训,每名志愿者可以选择参加一项培训.参加两项培训或不参加培训。已知参加过英语培训的有75%,参加过日语培训的有60%,假设每名志愿者对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
⑴从该高校志愿者中任选1名,求这人参加过本次口语培训的概率;
⑵从该高校志愿者中任选3名,求至少有2人参加过本次口语培训的概率.
17.(本小题满分10分)
已知:函数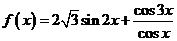
(1)求函数 的最大值及此时
的最大值及此时 的值;
的值;
(2)在 中,
中,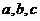 分别为内角
分别为内角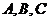 所对的边,且对
所对的边,且对 定义域中的任意的
定义域中的任意的 都有
都有 ,若
,若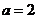 ,求
,求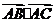 的最大值.
的最大值.
16.已知正四棱柱 的底面边长
的底面边长 ,侧棱长
,侧棱长 ,它的外接球的球心为
,它的外接球的球心为 ,点
,点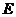 是
是 的中点,点
的中点,点 是球
是球 的球面上任意一点,有以下判断,(1)
的球面上任意一点,有以下判断,(1) 长的最大值是9;(2)三棱锥
长的最大值是9;(2)三棱锥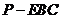 体积的最大值是
体积的最大值是 ;(3)存在过点
;(3)存在过点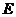 的平面,截球
的平面,截球 的截面面积是
的截面面积是 ;(4)三棱锥
;(4)三棱锥 体积的最大值是20.
体积的最大值是20.
其中正确答案的序号是____________________(写出所有正确答案的序号)
15.若非负实数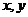 满足条件
满足条件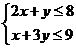 ,则
,则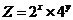 的最大值为_______________
的最大值为_______________
14.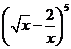 的展开式中含
的展开式中含 项的系数为_________________
项的系数为_________________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com