
24.(本小题满分10分)选修4-5:不等式选讲
已知函数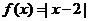 ,
, .
.
(Ⅰ)解关于 的不等式
的不等式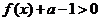 (
( );
);
(Ⅱ)若函数 的图象恒在函数
的图象恒在函数 图象的上方,求
图象的上方,求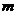 的取值范围.
的取值范围.
1--12 DACDBDBDDAAC
23.(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系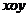 中,曲线
中,曲线 的参数方程为
的参数方程为 (
(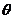 为参数),以坐标原点
为参数),以坐标原点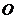 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,得曲线
轴的正半轴为极轴建立极坐标系,得曲线 的极坐标方程为
的极坐标方程为 (
(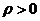 ).
).
(Ⅰ)化曲线 、
、 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)设曲线 与
与 轴的一个交点的坐标为
轴的一个交点的坐标为 (
(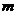 ,0)(
,0)( ),经过点
),经过点 作曲线
作曲线 的切线
的切线 ,求切线
,求切线 的方程.
的方程.
22.(本小题满分10分)选修4-1:几何证明选讲
 如图,在
如图,在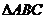 中,
中, ,以
,以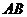 为直径的⊙O交
为直径的⊙O交 于
于 ,过点
,过点 作⊙O的切线交
作⊙O的切线交 于
于 ,
, 交⊙O于点
交⊙O于点 .
.
(Ⅰ)证明: 是
是 的中点;
的中点;
(Ⅱ)证明: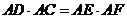 .
.
21.已知椭圆C的中心在原点,焦点在 轴上,左右焦点分别为
轴上,左右焦点分别为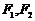 ,且
,且 ,点(1,
,点(1, )
)
在椭圆C上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点,且
两点,且 的面积为
的面积为 ,求以
,求以 为圆心
为圆心
且与直线 相切的圆的方程.
相切的圆的方程.
※考生注意:请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分.做答时,用2B铅笔在答题卡上把所选题目对应的题号涂黑.
20.已知正项数列 中,
中,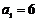 ,点
,点 在抛物线
在抛物线 上;数列
上;数列 中,点
中,点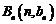 在过点
在过点 ,以方向向量为
,以方向向量为 的直线上.
的直线上.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若 ,问是否存在
,问是否存在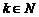 ,使
,使 成立,若存在,求出
成立,若存在,求出 值;若不存在,说明理由;
值;若不存在,说明理由;
(Ⅲ)对任意正整数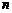 ,不等式
,不等式 成立,求正数
成立,求正数 的取值范围.
的取值范围.
19.如图,三棱柱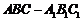 中,侧面
中,侧面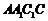
 底面
底面 ,
, ,
,
且 ,O为
,O为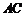 中点.
中点.
(Ⅰ)证明: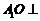 平面
平面 ;
;
(Ⅱ)求直线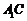 与平面
与平面 所成角的正弦值;
所成角的正弦值;
 (Ⅲ)在
(Ⅲ)在 上是否存在一点
上是否存在一点 ,使得
,使得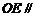 平面
平面 ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点 的位置.
的位置.
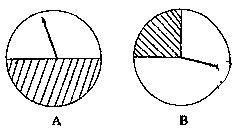
18.如图,两个圆形转盘A,B,每个转盘阴影部分各占转盘面积的 。某“幸运转盘积分活动”规定,当指针指到A,B转盘阴影部分时,分别赢得积分1000分和2000分。先转哪个转盘由参与者选择,若第一次赢得积分,可继续转为另一个转盘,此时活动结束,若第一次未赢得积分,则终止活动。
。某“幸运转盘积分活动”规定,当指针指到A,B转盘阴影部分时,分别赢得积分1000分和2000分。先转哪个转盘由参与者选择,若第一次赢得积分,可继续转为另一个转盘,此时活动结束,若第一次未赢得积分,则终止活动。
(1)记先转A转盘最终所得积分为随机量X,则X的取值分别是多少?
(2)如果你参加此活动,为了赢得更多的积分,你将选择先转哪个转盘?请说明理由。

17.已知函数 的
的
 部分图象如图所示.
部分图象如图所示.
(Ⅰ) 求函数 的解析式;
的解析式;
(Ⅱ)
如何由函数 的图象通过适当的变换得
的图象通过适当的变换得
到函数 的图象, 写出变换过程.
的图象, 写出变换过程.
16.某学生对函数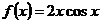 进行研究后,得出如下四个结论:
进行研究后,得出如下四个结论:
⑴函数 在
在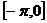 上单调递增,在
上单调递增,在 上单调递减;
上单调递减;
⑵存在常数 ,使
,使 对一切实数x均成立;
对一切实数x均成立;
⑶点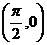 是函数
是函数 图像的一个对称中心;
图像的一个对称中心;
⑷函数 图像关于直线
图像关于直线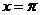 对称。其中正确的是 。(把你认为正确命题的序号都填上)
对称。其中正确的是 。(把你认为正确命题的序号都填上)
15. 已知 ,右边程序框图表示的是给定
,右边程序框图表示的是给定 的值,
的值,
求其函数值的算法.请将该程序框图补充完整.其中①处应
填 ,②处应填 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com