
区域内部具有一定的共同性或相关性,而区域与区域之间则存在着差异性。我国地域辽阔,各地自然地理环境差异明显。在自然环境方面,我国形成了特点各异的三大自然区。据此,回答1-3题:
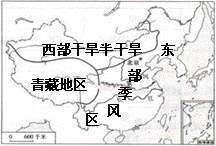 1.我国自然地理要素的分布规律,叙述正确的是( )
1.我国自然地理要素的分布规律,叙述正确的是( )
A.地形从西向东表现为山地-高原-平原
B.气温无论冬夏均为由南向北递减,等温线和
纬线大致平行
C.降水量从东南向西北递减
D.河流水量从北向南依次增大
2.下列关于三大自然区域内部差异性的叙述,错误的是( )
A.东部季风区内部差异的形成以热量为基础
B.西北干旱半干旱区内部差异的形成以水分为基础
C.青藏高寒区的垂直差异主要随海拔的升高而发生变化
D.三大自然区存在内部差异均以热量的变化为基础
3.下列有关三个经济地带发展的叙述,正确的是( )
①把部分劳动密集型加工企业逐步转移到中、西部
②把农牧产品加工企业逐步转移到东部
③优先安排东部地区基础设施和资源开发项目
④充分发挥三个地带各自的优势,实现协调发展
A.①② B.②③ C.①④ D.②④
6.自感现象
例题10.如图16所示, 、
、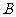 是两个完全相同的白炽灯泡,
是两个完全相同的白炽灯泡, 时是直流电阻不计的电感线圈,如果断开开关
时是直流电阻不计的电感线圈,如果断开开关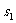 ,而闭合开关
,而闭合开关 ,
, 、
、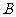 两灯都能同样发光。最初开关
两灯都能同样发光。最初开关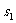 是闭合的,而
是闭合的,而 是断开的,则可能出现的情况是
是断开的,则可能出现的情况是
 .刚闭合
.刚闭合 时,
时, 灯立即发光,而
灯立即发光,而 灯则延迟一段时间才发光
灯则延迟一段时间才发光
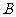 .刚闭合
.刚闭合 时,电感线圈
时,电感线圈 中的电流为零
中的电流为零
 .闭合
.闭合 以后,
以后, 灯立即发光并最终达到稳定,
灯立即发光并最终达到稳定,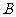 灯则由亮变暗直到熄灭
灯则由亮变暗直到熄灭
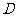 .闭合
.闭合 一段时间后,再断开
一段时间后,再断开 时,
时, 灯立即熄灭,而
灯立即熄灭,而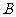 灯是
灯是 亮一下再熄灭
亮一下再熄灭
解析:在闭合开关 的瞬间,
的瞬间, 、
、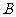 两灯虽然都立即发光,但由于电感线圈
两灯虽然都立即发光,但由于电感线圈 对交变电流的阻碍作用,开始时电感线圈
对交变电流的阻碍作用,开始时电感线圈 中的电流几乎为零,此时
中的电流几乎为零,此时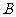 灯是最亮的。随着电路中的电流趋于稳定,电感线圈
灯是最亮的。随着电路中的电流趋于稳定,电感线圈 对电流的阻碍作用越来越小,通过
对电流的阻碍作用越来越小,通过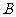 灯的电流随之越来越小,其亮度逐渐变暗,最终的结果是电感线圈
灯的电流随之越来越小,其亮度逐渐变暗,最终的结果是电感线圈 将
将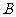 灯短路,即
灯短路,即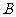 灯熄灭,与此同时,电路中的电流达到稳定,
灯熄灭,与此同时,电路中的电流达到稳定, 灯的亮度也同时达到了稳定。所以选项
灯的亮度也同时达到了稳定。所以选项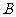 、
、 均正确。闭合
均正确。闭合 一段时间后,再断开
一段时间后,再断开 时,回路中通过
时,回路中通过 灯的电流立即变为零,所以
灯的电流立即变为零,所以 灯立即熄灭,而由于这时
灯立即熄灭,而由于这时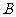 灯和电感线圈
灯和电感线圈 由组成一个新的闭合电路,电感线圈
由组成一个新的闭合电路,电感线圈 这时所起的作用是阻碍本身电流的减小,使得这个新的闭合电路中的电流只能从原来线圈
这时所起的作用是阻碍本身电流的减小,使得这个新的闭合电路中的电流只能从原来线圈 中的电流逐渐变小,不会立即消失,所以
中的电流逐渐变小,不会立即消失,所以 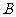 灯会亮一下再熄灭,选项
灯会亮一下再熄灭,选项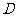 也是正确的。
也是正确的。
故,本题的答案为

 。
。
知识链接:
①自感现象是导体自身电流发生变化时而产生的一种电磁感应现象,分为通电自感和断电自感两种。
②电感线圈对变化的电流只是起到一种“阻碍电流变化”的作用,最终还是要达到“该达到的状态”,只是使该过程的时间“拉长”,通过做题要反复的理解这一点。
5.电磁感应规律的综合运用
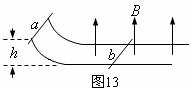 例题9.如图13所示,金属杆
例题9.如图13所示,金属杆 从离地高为
从离地高为 处从静止开始沿弧形轨道下滑,轨道平行的水平部分有竖直向上的磁感应强度为
处从静止开始沿弧形轨道下滑,轨道平行的水平部分有竖直向上的磁感应强度为 的匀强磁场,水平轨道足够长,其上原来放一个金属杆
的匀强磁场,水平轨道足够长,其上原来放一个金属杆 。已知杆
。已知杆 的质量为
的质量为 ,且与杆
,且与杆 的质量之比为
的质量之比为 ︰
︰ ︰
︰ ,不计一切摩擦,试求
,不计一切摩擦,试求
⑴ 和
和 的最终速度分别是多少?
的最终速度分别是多少?
⑵整个过程中释放的电能是多少?
⑶若已知杆 、
、 的电阻之比为
的电阻之比为 ︰
︰
 ︰
︰ ,其
,其 余电阻不计,则整个过程中产生的热量是多少?
余电阻不计,则整个过程中产生的热量是多少?
解析:⑴ 下滑
下滑 高度的过程中机械能守恒,则
高度的过程中机械能守恒,则

 进入磁场后,回路中产生感应电流,
进入磁场后,回路中产生感应电流, 、
、 都受安培力作用,
都受安培力作用, 做减速运动,而
做减速运动,而 则由静止开始加速,经过一段时间,
则由静止开始加速,经过一段时间, 、
、 速度达
速度达 到相同,之后回路的磁通量不再发生变化,感应电流为零,二者均做匀速运动,匀速运动的速度即为
到相同,之后回路的磁通量不再发生变化,感应电流为零,二者均做匀速运动,匀速运动的速度即为 、
、 的最终速度,设此速度为
的最终速度,设此速度为 。整个过程中动量守恒定律,则
。整个过程中动量守恒定律,则

解以上两式,得
 [来源:]
[来源:]
⑵由能量守恒定律可知,回路中产生的电能 等于
等于 、
、 系统机械能的损失,即
系统机械能的损失,即

⑶回路中产生的电能最终转化成为焦耳热释放出来,即

由于 、
、 两部分是串联的,通过它们的电流相等,所以有
两部分是串联的,通过它们的电流相等,所以有

故  ,
,
命题解读:
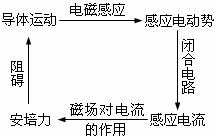
①这是一道电磁感应与磁场、导体的受力以及运动相结合的综合题目,题中的电磁感应现象、力现象相互联系而又相互制约,其关系如下
 这类题目综合程度高,涉及的知识面广,解题时可将问题分解为电学和力学两部分,其应对思路分别为
这类题目综合程度高,涉及的知识面广,解题时可将问题分解为电学和力学两部分,其应对思路分别为
电学部分:一是将产生感应电动势的那部分电路等效为电源,如果电路中有几个这样的电源 ,要看清楚它们的串、并联关系;二是分清内外电路,利用闭合电路的欧姆定律(或部分电路欧姆定律)解决个电学量之间的关系。
,要看清楚它们的串、并联关系;二是分清内外电路,利用闭合电路的欧姆定律(或部分电路欧姆定律)解决个电学量之间的关系。
力学部分:分析通电导体的受力情况,应用牛顿定律、动能定理、动量定理或动量守恒定律、解械能守恒定律等解决力学量之间的关系。
②本题需要 注意的问题有:一是要理解“最终速度”的含义;二是要注意,安培力对于每一根金属杆来讲是外力,而对于
注意的问题有:一是要理解“最终速度”的含义;二是要注意,安培力对于每一根金属杆来讲是外力,而对于 、
、 组成的系统而言则成了内力。
组成的系统而言则成了内力。
 对应训练:如图14所示,水平水面内固定两平行的光滑导轨,左边两导轨间的距离为
对应训练:如图14所示,水平水面内固定两平行的光滑导轨,左边两导轨间的距离为 ,右边两导轨间的距离为
,右边两导轨间的距离为 ,左、右两部分用导体材料连接,两导轨轨间都存在磁感应强度为
,左、右两部分用导体材料连接,两导轨轨间都存在磁感应强度为 、方向竖直向下的匀强磁场。两均匀的导体棒
、方向竖直向下的匀强磁场。两均匀的导体棒 和
和 分别垂直放在左、右两边的轨道之间,
分别垂直放在左、右两边的轨道之间, 棒的质量为
棒的质量为
 ,电阻为
,电阻为 ,而
,而 棒的质量为
棒的质量为 ,电阻为
,电阻为 ,其它部分的电阻不计。原来两棒都处于静止状态,现
,其它部分的电阻不计。原来两棒都处于静止状态,现 棒在沿导轨向右的水平恒力
棒在沿导轨向右的水平恒力 作用下开始运动,设两导轨足够长,两棒都不会滑出各自的轨道。
作用下开始运动,设两导轨足够长,两棒都不会滑出各自的轨道。
⑴试分析两棒最终达到何种稳定状态?此状态下两棒的加速度各是多大?
⑵在达到稳定状态时, 棒产生的热功率多大?
棒产生的热功率多大?
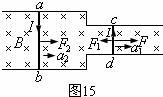 解析:⑴
解析:⑴ 棒由静止开始向右运动,产生如图15所
棒由静止开始向右运动,产生如图15所 示的感应电流,设此电流大小为
示的感应电流,设此电流大小为 ,
, 和
和 棒受到的安培力分别为
棒受到的安培力分别为 和
和 ,速度分别为
,速度分别为 和
和 ,加速度分别为
,加速度分别为 和
和 ,则
,则

 ,
,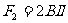
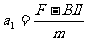 ,
,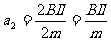
开始阶段安培力小, >
>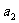 ,
, 棒比
棒比 棒速速变化得快,随着(
棒速速变化得快,随着( )的增大,
)的增大, 和
和 均增大,
均增大, 减小,而
减小,而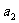 增大。当
增大。当 =2
=2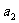 时,(
时,( )不再变化,
)不再变化, 不变,
不变, 和
和 也不再变化,两棒以不同的加速度做匀加速运动,所以最终两棒的加速度为
也不再变化,两棒以不同的加速度做匀加速运动,所以最终两棒的加速度为
 ,
,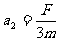
⑵两棒最终处于匀加速运动状态时,有 =2
=2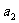 ,解得
,解得
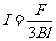
此时 棒产生的焦耳热功率为
棒产生的焦耳热功率为

误点警示:
此题是根据受力分析判断两金属棒的运动性质,需要注意的就是两棒最终的稳定状态是各自以不同的加速度做匀加速运动,回路中还有恒定的感应电流,这点上与上面的例题是不同的。
4.电磁感应中的能量守恒问题
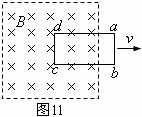
例题7.如图11所示,把一矩形线圈 从有理想边界的匀强磁场中拉出,第一次速度为
从有理想边界的匀强磁场中拉出,第一次速度为 ,第二次速度为
,第二次速度为 ,且
,且 。则在两种情况下,拉力做功之比为
。则在两种情况下,拉力做功之比为 ︰
︰ ________,拉力的功率之比为
________,拉力的功率之比为 ︰
︰ ________,线圈中产生的焦耳热之比为
________,线圈中产生的焦耳热之比为 ︰
︰ ________。
________。
解析:设矩形线圈的 边长为
边长为 ,
, 边长为
边长为 ,整个线圈的电阻为
,整个线圈的电阻为 。以速度
。以速度 将线圈匀速拉出磁场时,
将线圈匀速拉出磁场时, 边切割磁感线产生的感应电动势大小为
边切割磁感线产生的感应电动势大小为

其方向由 ,线圈中形成的感应电流为
,线圈中形成的感应电流为

因是将线圈匀速拉出磁场,故所需外力大小等于 边所受的安培力,即为
边所受的安培力,即为

整理以上几式,得

因此,外力的功、功率以及线圈中产生的焦耳热分别为



从而得出下面的结论
 ︰
︰
 ︰
︰ ,
, ︰
︰
 ︰
︰ ,
, ︰
︰
 ︰
︰ 。
。
命题解读:
①由以上的计算可以推知,外力克服安培力所做的功等于电路中所产生的电能,这是一个很重要的结论。
②匀速将线圈拉出磁场时,外力做功将机械能全部转化为了线圈中的电能,最后又转化为了内能,并以焦耳热的形式释放出来,符合能量守恒定律。
 ③若是将线圈加速拉出呢?从量守恒的角度讲,外力做功则是将机械能转化为线圈中的电能以及线圈本身动能的增加量。
③若是将线圈加速拉出呢?从量守恒的角度讲,外力做功则是将机械能转化为线圈中的电能以及线圈本身动能的增加量。
类似于上面的讨论,利用能量守恒定律可以对电磁感应中的能量的转化情况进行快速的推理或判断,请看下面的例题:
例题8.两根光滑的金属导轨,平行放置在倾角为 的斜面上,导轨的左端接有电阻
的斜面上,导轨的左端接有电阻 ,导轨自身的电阻可忽略不计。斜面处在一匀强磁场中,磁场方向垂直于斜面向上。质量为
,导轨自身的电阻可忽略不计。斜面处在一匀强磁场中,磁场方向垂直于斜面向上。质量为 、电阻不计的金属棒
、电阻不计的金属棒 ,在沿着斜面、与棒
,在沿着斜面、与棒 垂直的恒力
垂直的恒力 作用下沿导轨匀速上升,上升高度为
作用下沿导轨匀速上升,上升高度为 ,如图12所示。则在此过程中
,如图12所示。则在此过程中
 .作用于棒
.作用于棒 上的各力的合力所做的功等于零
上的各力的合力所做的功等于零
 .恒力
.恒力 和重力的合力所做的功等于电阻
和重力的合力所做的功等于电阻 上产生的焦耳热
上产生的焦耳热
 .恒力
.恒力 和安培力的合力所做的功等于零
和安培力的合力所做的功等于零
 .恒力
.恒力 所做的功等于棒
所做的功等于棒 重力势能的增加量和电阻
重力势能的增加量和电阻 上产生的焦耳热之和
上产生的焦耳热之和
解析:在金属棒 沿斜面上升的过程中,除重力和外力
沿斜面上升的过程中,除重力和外力 对它做功外,还有感应电流所受的安培力做功,由动能定理得
对它做功外,还有感应电流所受的安培力做功,由动能定理得

显然,根据上式可以判断出选项 正确,而
正确,而 是错
是错 误的。
误的。
把上式移项,得

而 为杆
为杆 克服安培力所做的功,正好等于电路中所产生的焦耳热,故选项
克服安培力所做的功,正好等于电路中所产生的焦耳热,故选项 也正确。
也正确。
另一方面,从能量守恒的角度可知,金属杆 上升的过程中,其重力势能增加,同时电路中产生了电能,这些能量从哪里来呢?只能是外力
上升的过程中,其重力势能增加,同时电路中产生了电能,这些能量从哪里来呢?只能是外力 做功的结果,通过外力
做功的结果,通过外力 做功,将其它形式的能量转化成了这两这两种形式的能量。所以选项
做功,将其它形式的能量转化成了这两这两种形式的能量。所以选项 也是正确的。其实,判断选项
也是正确的。其实,判断选项 时,也可以通过对等式
时,也可以通过对等式 移项得出结论。
移项得出结论。
故,本题的正确选项为

 。
。
命题解读:
凡涉及做功和能量的转化等问题时,一般采取的措施就是利用动能定理和普遍适用的能量守恒定律进行讨论。
3.感应电动势大小的计算
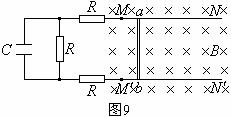
例题5.(07天津理综)两根光滑的长直导轨 、
、 平行置于同一水平面内,导轨间距为
平行置于同一水平面内,导轨间距为 ,其电阻不计,
,其电阻不计, 、
、 处接有如图9所示所示的电路,电路中各电阻的阻值均为
处接有如图9所示所示的电路,电路中各电阻的阻值均为 ,电容器的电容为
,电容器的电容为 。长度也为
。长度也为 、电阻同为
、电阻同为 的金属棒
的金属棒 垂直于导轨放置,导轨处在磁感应强度为
垂直于导轨放置,导轨处在磁感应强度为 、方向竖直向下的匀强磁场中。金属棒
、方向竖直向下的匀强磁场中。金属棒 在外力作用下向右匀速运动且与导轨保持良好接触,在
在外力作用下向右匀速运动且与导轨保持良好接触,在 运动距离为
运动距离为 的过程中,整个回路中产生的焦耳热为
的过程中,整个回路中产生的焦耳热为 。试求:
。试求:
 ⑴金属棒
⑴金属棒 运动速度
运动速度 的大小;
的大小;
⑵电容器所带的电荷量。
解析:⑴设 产生的感应电动势为
产生的感应电动势为 ,回路中的电流为
,回路中的电流为 ,
, 运动距离
运动距离 所用的时间为
所用的时间为 ,则有
,则有



 [来源:Z|X|X|K]
[来源:Z|X|X|K]
解以上方程,得

⑵设电容器两极板间的电势差为 ,则有
,则有

电容器所带电量为

解得 
知识链接:
①导体切割磁感线时,一般用公式 计算感应电动势大小。最适宜的情况是整个过程中切割磁感线的速度
计算感应电动势大小。最适宜的情况是整个过程中切割磁感线的速度 不变,若速度
不变,若速度 是随时变化的,可以把某一瞬时的速度代入求出那一瞬时的感应电动势。
是随时变化的,可以把某一瞬时的速度代入求出那一瞬时的感应电动势。
②切割磁感线产生感应电动势的导体相当于电源,象本题中的金属棒 ,它与几个定值电阻、电容器构成闭合电路,这样就可以利用闭合电路的欧姆定律计算电路中的电流、电量、电热、电功等。
,它与几个定值电阻、电容器构成闭合电路,这样就可以利用闭合电路的欧姆定律计算电路中的电流、电量、电热、电功等。
③在这道题目中,感应电动势大小恒定,使得感应电流的大小也恒定不变,计算电量、电热或电功都可以用同一个值。如果电流是随时变化的,象交流电部分,那就要区分了,计算电量用的时电流的平均值,而计算电热、电功等用的则是交流电的有效值。
 例题6.如图10所示,平行的光滑金属导轨
例题6.如图10所示,平行的光滑金属导轨 和
和 相距
相距 ,处于同一竖直平面内,
,处于同一竖直平面内, 间接有阻值为
间接有阻值为 的电阻,轻质金属杆
的电阻,轻质金属杆 长为
长为 ,紧贴导轨竖直放置,离
,紧贴导轨竖直放置,离 端
端 处固定有质量为
处固定有质量为 的小球。整个装置处于磁感应强度为
的小球。整个装置处于磁感应强度为 并于导轨平面垂直的匀强磁场中,当金属杆
并于导轨平面垂直的匀强磁场中,当金属杆 由静止开始竖贴导轨并饶
由静止开始竖贴导轨并饶 端向右倒下至水平位置时,小球的速度为
端向右倒下至水平位置时,小球的速度为 。若导轨足够长,导轨及金属杆电阻不计,试求此过程中
。若导轨足够长,导轨及金属杆电阻不计,试求此过程中
⑴通过电阻 的电量;
的电量;
⑵ 中的最大电流。
中的最大电流。
解析:当金属杆 向右倒下且
向右倒下且 端离开
端离开 之前,闭合电路中的磁通量发生变化,
之前,闭合电路中的磁通量发生变化, 中有感应电流通过;当
中有感应电流通过;当 端离开
端离开 之后,电路不再闭合,
之后,电路不再闭合, 中不再有感应电流通过。通过
中不再有感应电流通过。通过 的电量应与单位时间内通过电路的平均电流有关。在
的电量应与单位时间内通过电路的平均电流有关。在 倒下的过程中,其切割磁感线的“有效长度”及切割速度均逐渐增大,因此,
倒下的过程中,其切割磁感线的“有效长度”及切割速度均逐渐增大,因此, 将要滑离
将要滑离 的瞬间,
的瞬间, 中的电流最大。
中的电流最大。
⑴ 滑离
滑离 之前,电路中的磁通量的变化为
之前,电路中的磁通量的变化为
 [来源:]
[来源:]
这段时间 内的平均感应电动势为
内的平均感应电动势为


平均电流为

所以,通过电阻 的电量为
的电量为

解以上几式,得

⑵ 滑离
滑离 的瞬间,电路中的电流为
的瞬间,电路中的电流为

而 
式中的 指的是滑离
指的是滑离 的瞬间
的瞬间 杆切割磁感线的平均速度,它等于
杆切割磁感线的平均速度,它等于 杆中点的速度,应该是此时小球速度的两倍。因
杆中点的速度,应该是此时小球速度的两倍。因 滑离
滑离 后电路中不再有电流
后电路中不再有电流 ,
, 倒下的过程中只有重力做功,机械能守恒,即
倒下的过程中只有重力做功,机械能守恒,即

解以上几式,得

命题解读:
①因穿过电路的磁通量 变化而发生电磁感应现象时,通常用法拉第电磁感应定律计算感应电动势,此定律适宜的情况是某一过程,所以利用此式计算出的是该段时间内感应电动势的平均值,由此而计算出的电流也是平均值,可以用来计算电量,不能用来计算电热、电功等。从上面的第一问列出的几式可以看出,感应电流通过电路的电量
变化而发生电磁感应现象时,通常用法拉第电磁感应定律计算感应电动势,此定律适宜的情况是某一过程,所以利用此式计算出的是该段时间内感应电动势的平均值,由此而计算出的电流也是平均值,可以用来计算电量,不能用来计算电热、电功等。从上面的第一问列出的几式可以看出,感应电流通过电路的电量 (
( 为线圈的匝数)是一个普遍适用得计算式。
为线圈的匝数)是一个普遍适用得计算式。
 ②解决此题时需要注意的两个关键位置:一是要分析出
②解决此题时需要注意的两个关键位置:一是要分析出 杆切割磁感线的“有效长度”和平均速度均越来越大,从而得出“
杆切割磁感线的“有效长度”和平均速度均越来越大,从而得出“ 将要滑离
将要滑离 的瞬间,
的瞬间, 中的电流最大”;二是分析得出
中的电流最大”;二是分析得出 杆滑离
杆滑离 后,电路中不再有电流产生,以后的过程中小球的机械能守恒,这也是解决
后,电路中不再有电流产生,以后的过程中小球的机械能守恒,这也是解决 杆最大切割速度,产生最大感应电流的非常重要的一步。
杆最大切割速度,产生最大感应电流的非常重要的一步。
2. 感应电流的产生及方向的判断
感应电流的产生及方向的判断
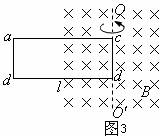
例题3.如图3所示,闭合的矩形金属线框 仅有一半置于范围足够大的匀强磁场中,开始时线框平面与磁场垂直,现从图示位置绕轴
仅有一半置于范围足够大的匀强磁场中,开始时线框平面与磁场垂直,现从图示位置绕轴 按图示方向转动,线框中有感应电流产生吗?试加以分析。
按图示方向转动,线框中有感应电流产生吗?试加以分析。
 解析:由于开始时线框仅有一半处于磁场中,所以在
解析:由于开始时线框仅有一半处于磁场中,所以在 边进入磁场之前,穿过线框的磁通量是发生不变化的,所以这一阶段线框中无感应电流产生。只有当线框转过
边进入磁场之前,穿过线框的磁通量是发生不变化的,所以这一阶段线框中无感应电流产生。只有当线框转过 角,即从
角,即从 边进入磁场开始,穿过线圈的磁通量才发生变化,如图4所示(俯视图)。但随着线框在磁场中的转动,
边进入磁场开始,穿过线圈的磁通量才发生变化,如图4所示(俯视图)。但随着线框在磁场中的转动, 一旦线框的
一旦线框的 边转出磁场,穿过线框的磁通量又不发生变化了,电磁感应现象又消失了,以后将重复上述过程。
边转出磁场,穿过线框的磁通量又不发生变化了,电磁感应现象又消失了,以后将重复上述过程。
综上所述,只有线框全部转入磁场中时,才会有感应电流产生,否则没有。
知识链接与误点警示:
①产生感应电流的条件是“穿过闭合电路的磁通量发生变化”,即,要产生感应电流,必须同时满足两个条件,一个是电路闭合,另一个则是穿过电路的磁通量发生变化。
②磁通量的计算公式是: ,式中的
,式中的 应是磁场区域内线框平面在垂直于磁场方向上的投影(面积)大小。所以此题的讨论中,千万不要误认为线框从开始运动就有感应电流产生。一定要记住:磁通量的实质是穿过某一面的磁感线的条数!
应是磁场区域内线框平面在垂直于磁场方向上的投影(面积)大小。所以此题的讨论中,千万不要误认为线框从开始运动就有感应电流产生。一定要记住:磁通量的实质是穿过某一面的磁感线的条数!
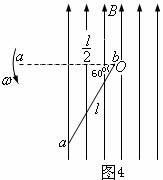
 例题4.如图5所示,导线框
例题4.如图5所示,导线框 与导线
与导线 在同一平面内,直导线中通有恒定电流
在同一平面内,直导线中通有恒定电流 ,在线框由左向右匀速通过直导线的过程中,线框中感应电流的方向是
,在线框由左向右匀速通过直导线的过程中,线框中感应电流的方向是
 .先
.先 ,再
,再 ,后
,后
 .先
.先 ,再
,再
 .始终
.始终
 .先
.先 ,再
,再 ,后
,后
解析(一):由左手定则判断
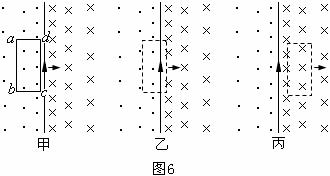 线框向右运动时,只有
线框向右运动时,只有 和
和 两个边切割磁感线。根据通电导线
两个边切割磁感线。根据通电导线 周围磁场的分布情况可知,开始时,即在
周围磁场的分布情况可知,开始时,即在 边越过通电导线
边越过通电导线 之前(如图6甲图所示),
之前(如图6甲图所示), 和
和 边以相同的速度切割磁感线,由左手定则可以判断,它们在闭合线框中形成的感应电流方向相反,即分别是逆时针和顺时针的。但由于
边以相同的速度切割磁感线,由左手定则可以判断,它们在闭合线框中形成的感应电流方向相反,即分别是逆时针和顺时针的。但由于 边所在处的磁感应强度大,所以此时感应电流的方向是顺时针方向的,即
边所在处的磁感应强度大,所以此时感应电流的方向是顺时针方向的,即 。一旦
。一旦 边开始越过通电导线
边开始越过通电导线 (如图6乙所示),根据
(如图6乙所示),根据 和
和 边所在处的磁感应强度的方向和强弱,由左手定可可以判断得出此时线框中的感应电流的方向是逆时针方向的,即
边所在处的磁感应强度的方向和强弱,由左手定可可以判断得出此时线框中的感应电流的方向是逆时针方向的,即 。随着线框继续向右运动,
。随着线框继续向右运动, 边越过通电导线
边越过通电导线 后(如图6丙所示),同理可以判断出此时线框中的感应电流的方向是顺时针方向的,即
后(如图6丙所示),同理可以判断出此时线框中的感应电流的方向是顺时针方向的,即 。
。
综合以上分析,答案应选 。
。
解析(二):由楞次定律判断
通电导线 所产生的磁场,在
所产生的磁场,在 的左侧方向是垂直纸面向外的,而在
的左侧方向是垂直纸面向外的,而在 的右侧方向是垂直纸面向里的,并且离导线越近磁场越强,如图6所示。线框开始向右运动时,
的右侧方向是垂直纸面向里的,并且离导线越近磁场越强,如图6所示。线框开始向右运动时, 由图甲可以看出,穿过线框的向外的磁通量是逐渐增加的,根据楞次定律可以判断出此时线框中的感应电流方向是
由图甲可以看出,穿过线框的向外的磁通量是逐渐增加的,根据楞次定律可以判断出此时线框中的感应电流方向是 。一旦线框的
。一旦线框的 边越过通电导线
边越过通电导线 ,如图乙所示,穿过线框的磁通量既有向外的,也有向里的,并且向外的磁通量减小,而向里的磁通量增加,由楞次定律可以判断出这一过程中线框中的感应电流方向是
,如图乙所示,穿过线框的磁通量既有向外的,也有向里的,并且向外的磁通量减小,而向里的磁通量增加,由楞次定律可以判断出这一过程中线框中的感应电流方向是 。随着线框继续向右运动,当它的
。随着线框继续向右运动,当它的 边越过通电导线
边越过通电导线 后,穿过线框的磁通量就只有垂直纸面向里的了,并且在逐渐减小,由楞次定律判断出线框中感应电流的方向是
后,穿过线框的磁通量就只有垂直纸面向里的了,并且在逐渐减小,由楞次定律判断出线框中感应电流的方向是 。
。
综合以上分析,答案应选 。
。
知识链接:感应电流方向的判断,既可用右手定则 ,也可用楞次定律:
,也可用楞次定律:
①右手定则:适合于判断导线切割磁感线的情形。用右手定则判断感应电流的方向不要仅仅停留在应用上,还要对电流的形成理解其实质,即导线中的自由电子随导线一起做定向运动,于是在洛仑兹力的作用下就会发生定向移动形成电流。即,在利用右手定则的同时,也要和左手定则进行联系。
 ②楞次定律:适合于判断磁通量发生变化时的情形。应用次定律时,一定要正确理解定律中“阻碍”二字的深刻含义,“阻碍”的并不是磁通量,而是磁通量的变化!即,感应电流的磁场方向并不总是和“引起感应电流的磁场方向”相反的!当“穿过电路的磁通量增加时”,感应电流的磁场方向就和“引起感应电流的磁场方向”相反,否则就相同。
②楞次定律:适合于判断磁通量发生变化时的情形。应用次定律时,一定要正确理解定律中“阻碍”二字的深刻含义,“阻碍”的并不是磁通量,而是磁通量的变化!即,感应电流的磁场方向并不总是和“引起感应电流的磁场方向”相反的!当“穿过电路的磁通量增加时”,感应电流的磁场方向就和“引起感应电流的磁场方向”相反,否则就相同。
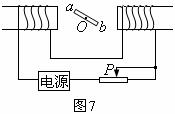
变式训练1:如图7所示, 是一个可以绕垂直于纸面的轴
是一个可以绕垂直于纸面的轴 转动的闭合矩形线框,当滑动变阻器的滑片
转动的闭合矩形线框,当滑动变阻器的滑片 自左向右滑动时,从纸外向纸内看,线框
自左向右滑动时,从纸外向纸内看,线框 将
将
 .保持不动
.保持不动
 .逆时针转动
.逆时针转动
 .顺时针转动
.顺时针转动
 .发生转动,但因电源极性不明确,无法判断转动方向
.发生转动,但因电源极性不明确,无法判断转动方向
解析:由于滑动变阻器的滑片 自左向右滑动,使得电路中的电流变小,因此穿过线框
自左向右滑动,使得电路中的电流变小,因此穿过线框 的磁通量变小,虽然不知道穿过线框的磁通量的方向,但由于感应电流的磁场总是阻碍引起感应电流的磁通量的变化,所以线框只有绕轴
的磁通量变小,虽然不知道穿过线框的磁通量的方向,但由于感应电流的磁场总是阻碍引起感应电流的磁通量的变化,所以线框只有绕轴 顺时针转动才能达到阻碍磁通量减小的目的,故本题答案为
顺时针转动才能达到阻碍磁通量减小的目的,故本题答案为 。
。
 变式训练2:如图8所示,在一绝缘支架的横梁两端,分别固定一个大小、形状、材料都一样的金属圆环
变式训练2:如图8所示,在一绝缘支架的横梁两端,分别固定一个大小、形状、材料都一样的金属圆环 和
和 ,只是
,只是 是闭合的,而
是闭合的,而 上有一个小的缺口,并且横梁和两金属环在同一平面上,横梁是可绕支点
上有一个小的缺口,并且横梁和两金属环在同一平面上,横梁是可绕支点 在水平面内转动的,原来静止不动。现将一条形磁铁分别去靠近并插向金属圆环
在水平面内转动的,原来静止不动。现将一条形磁铁分别去靠近并插向金属圆环 和
和 ,试分析各出现什么现象?
,试分析各出现什么现象?
解析:将条形磁铁靠近并插向闭合金属圆环 时,穿过环
时,穿过环 的磁通量增加,根据楞次定律,环
的磁通量增加,根据楞次定律,环 中感应电流的磁场为了阻碍该磁通量的增加,便会出现环
中感应电流的磁场为了阻碍该磁通量的增加,便会出现环 与条形磁铁同向运动的情形,从上向下看,横梁带着两金属环是逆时针转动的,即出现了“感应电流的磁场阻碍磁铁和金属环
与条形磁铁同向运动的情形,从上向下看,横梁带着两金属环是逆时针转动的,即出现了“感应电流的磁场阻碍磁铁和金属环 之间的相对运动”现象;而当磁铁靠近并插向有缺口的环
之间的相对运动”现象;而当磁铁靠近并插向有缺口的环 时,由于环
时,由于环 不闭合,虽然有磁通量的变化,但并没有感应电流产生,所以此时横梁是不动的。
不闭合,虽然有磁通量的变化,但并没有感应电流产生,所以此时横梁是不动的。
命题解读:从这两道题目可以看出,利用楞次定律不仅可以判断感应电流的方向,而且利用上面的题目中总结出的“感应电流的磁场总阻碍物体之间的相对运动”这个结论,去直接判断线框、导体或磁体的的转动、运动或收缩等情况。
1.磁通量概念:
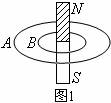 例题1.如图1所示,面积大小不等的两个圆形线圈
例题1.如图1所示,面积大小不等的两个圆形线圈 和
和 共轴套在一条形磁铁上,则穿过
共轴套在一条形磁铁上,则穿过 、
、 磁通量的大小关系是
磁通量的大小关系是 ____
____ 。
。
答案:<
知识链接:
①磁通量 的实质就是穿过某面积的磁感线的条数。磁铁内部向上的磁感线的总条数是相同的,但由于线圈
的实质就是穿过某面积的磁感线的条数。磁铁内部向上的磁感线的总条数是相同的,但由于线圈 的面积大于
的面积大于 的,外部穿过线圈向下的磁感线的条数
的,外部穿过线圈向下的磁感线的条数 的大于
的大于 的,所以
的,所以 <
< 。
。
②磁感线除了有大小以外,还有方向,但它是个标量。磁通量的方向仅仅表示磁感线沿什么方向穿过某面积,其运算不满足矢量合成的平行四边形定则,只满足代数运算。
③由磁通量的定义 可得:
可得: ,此式表示“磁感应强度
,此式表示“磁感应强度 大小等于穿过垂直于磁场方向的单位面积的磁感线条数”,所以磁感应强度又被叫做“磁感密度”。
大小等于穿过垂直于磁场方向的单位面积的磁感线条数”,所以磁感应强度又被叫做“磁感密度”。
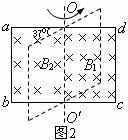 例题2.如图2所示,边长为
例题2.如图2所示,边长为 的正方形闭合线圈置于磁场中,线圈的
的正方形闭合线圈置于磁场中,线圈的 、
、 两边中点连线
两边中点连线 的左右两侧分别存在着方向相同、磁感应强度大小各为
的左右两侧分别存在着方向相同、磁感应强度大小各为 、
、 的匀强磁场。开始时,线圈平面与磁场垂直,若从上往下看,线圈逆时针转
的匀强磁场。开始时,线圈平面与磁场垂直,若从上往下看,线圈逆时针转 和
和 角时,穿过线圈的磁通量分别改变了多少?
角时,穿过线圈的磁通量分别改变了多少?
解析:在开始位置,线圈与磁场垂直,则



线圈绕 转动
转动 角后
角后



磁通量的变化量为

线圈绕 转动
转动 角时,若规定穿过圆线圈平面的磁通量为正,转过
角时,若规定穿过圆线圈平面的磁通量为正,转过 后,穿过线圈的磁通量则为负值,即
后,穿过线圈的磁通量则为负值,即



磁通量的变化量为

命题解读:
磁通量是有方向的,所以在求其变化量时,事先要设正方向,并将“+”、“-”号代入。否则,象上面的题目中,转过 角时的磁通量的变化量就变成了零!
角时的磁通量的变化量就变成了零!
22.(本题满分12分)
已知:平面α、β、γ,且α∩β﹦a, β∩ γ﹦b, γ∩α﹦c,
求证: 、
、 、
、 交于一点或互相平行。
交于一点或互相平行。
河北省六中2010届高二下学期第三次月考(数学)
21.(本题满分12分)
 已知长方体
已知长方体 中,
中, ,
, ,
, 分别为
分别为 和
和 的中点,
的中点, 为下底面正方形的中心。
为下底面正方形的中心。
(Ⅰ)证明: ⊥
⊥ ;
;
(Ⅱ)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
20. (本题满分12分)
(本题满分12分) 是正三角形
是正三角形 所在平面外一点,如右图,
所在平面外一点,如右图, ,且
,且 ,
, 分别是
分别是 和
和 的中点,求异面直线
的中点,求异面直线 和
和 所成角。
所成角。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com