22、(本小题满分12分)双曲线的离心率为，右准线为。

(Ⅰ)求双曲线C的方程；

(Ⅱ)已知直线与双曲线C交于不同的两点A，B，且线段AB的中点在圆上，求m的值.　

21、(理)已知是函数的一个极值点。

(Ⅰ)求的值；

(Ⅱ)求函数的单调区间；

21、(本小题满分12分)(文)设函数，其中常数a>1

(Ⅰ)讨论f(x)的单调性;

(Ⅱ)若当x≥0时，f(x)>0恒成立，求a的取值范围。

20、(本小题满分12分)如图，直三棱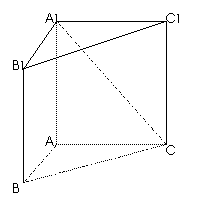柱中， AB=1，，∠ABC=60.

(Ⅰ)证明：；

(Ⅱ)求二面角A--B的大小。　

19、(理)数列的前项和记为

(Ⅰ)求的通项公式；

(Ⅱ)等差数列的各项为正，其前项和为，且，又成等比数列，求

19、(本小题满分12分)(文)甲、乙二人进行一次围棋比赛，约定先胜3局者获得这次比赛的胜利，比赛结束。假设在一局中，甲获胜的概率为0.6，乙获胜的概率为0.4，各局比赛结果相互独立。已知前2局中，甲、乙各胜1局。

(Ⅰ)求再赛2局结束这次比赛的概率；

(Ⅱ)(文)求甲获得这次比赛胜利的概率。

18、(理)设进入某商场的每一位顾客购买甲种商品的概率为，购买乙种商品的概率为，且购买甲种商品与购买乙种商品相互独立，各顾客之间购买商品也是相互独立的。

　(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率；

(Ⅱ)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率；

(Ⅲ)记表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数，求的分布列及期望。

18、(本小题满分12分)(文)已知向量m=(sinA,cosA),n=，m·n＝1，且A为锐角.

(Ⅰ)求角A的大小；(Ⅱ)求函数的值域.

17、(理)已知向量m=(sinA,cosA),n=，m·n＝1，且A为锐角.

(Ⅰ)求角A的大小；(Ⅱ)求函数的值域.

17、(本小题满分10分)(文)等差数列中，且成等比数列，求数列前20项的和．