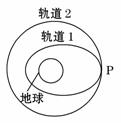
4. (2010德州一模)我国于2010年1月17日凌晨在西昌成功发射第三颗北斗导航卫星，此前，我国已成功发射了两颗北斗导航卫星，这次发射的北斗导航卫星(COMPASS－G2)是一颗地球同步卫星。如图所示，假若第三颗北斗导航卫星先沿椭圆轨道1飞行，后在远地点P处点火加速，由椭圆轨道1变成地球同步圆轨道2。下列说法正确的是：

A. 第三颗北斗导航卫星在轨道2运行时的速度大于7.9km/s

B. 第三颗北斗导航卫星在轨道2运行时不受重力作用

C. 第三颗北斗导航卫星在轨道2运行时的向心加速度比在赤道上相对地球静止的物体的向心加速度小

D. 第三颗北斗导航卫星在轨道1上的P点和轨道2上的P点的加速度大小相等

3. (2007年)22. 2007年4月24日，欧洲科学家宣布在太阳系之外发现了一颗可能适合人类居住的类地行星Gliese581c。这颗围绕红矮星Gliese 581运行的星球有类似地球的温度，表面可能有液态水存在，距离地球约为20光年，直径约为地球的1.5倍，质量约为地球的5倍.绕红矮星Gliese 581运行的周期约为13天。假设有一艘宇宙飞船飞临该星球表面附近轨道，下列说法正确的是

A. 飞船在Gliese 581c表面附近运行的周期约为13天

B. 飞船在Gliese 581c表面附近运行时的速度大于7.9km/s

C. 人在Gliese 581c上所受重力比在地球上所受重力大

D.　 Gliese 581c的平均密度比地球平均密度小

2010山东各地模拟

2. (2008年)18. 据报道，我国数据中继卫星“天链一号01星”于2008年4月25日在西昌卫星发射中心发射升空，经过4次变轨控制后，于5月1日成功定点在东经77赤道上空的同步轨道。关于成功定点后的“天链一号01星”，下列说法正确的是

A. 运行速度大于7.9 km/s

B. 离地面高度一定，相对地面静止

C. 绕地球运行的角速度比月球绕地球运行的角速度大

D. 向心加速度与静止在赤道上物体的向心加速度大小相等

1. (2009年)18. 2008年9月25日至28日我国成功实施了“神舟”七号载入航天飞行并实现了航天员首次出舱。飞船先沿椭圆轨道飞行，后在远地点343千米处点火加速，由椭圆轨道变成高度为343千米的圆轨道，在此圆轨道上飞船运行周期约为90分钟。下列判断正确的是

A．飞船变轨前后的机械能相等

　 　B．飞船在圆轨道上时航天员出舱前后都处于失重状态

　 　C．飞船在此圆轨道上运动的角速度大于同步卫星运动的角速度

　 　D．飞船变轨前通过椭圆轨道远地点时的加速度大于变轨后沿圆轨道运动的加速度

22、(本小题满分14分)

解(1)∵函数图象关于原点对称，∴对任意实数，　 1分

，即恒成立，

，　

．　 3分

∵ x = 1时，取极小值－，

∴ 3a + c = 0且a + c = －，

解得a = ，c = －1．　 5分

　 (2)当时，图象上不存在这样的两点使结论成立．　 6分

假设图象上存在两点、，使得过此两点处的切线互相垂直，

则由知两点处的切线斜率分别为，

且…………(*)　 8分

∵x₁、，，　

此与(*)相矛盾，故假设不成立．　 9分

(3)证明：f^/(x) = x²－1，令f^/(x) = 0，得x = ±1，

∵ x Î (－¥,－1)或x Î (1, + ¥)时，f^/(x)>0；x Î (－1,1)时，f^/(x)<0，　 10分

上是减函数，且，　 11分

∴在[－1，1]上，有| f(x) |≤成立，　　 12分

于是当x­₁，x₂ Î [－1,1]时，．　 14分

21、(本小题满分12分)

解：(1) 由a₂ = 6，= 1，= 2，= 3，　 1分

解得a­₁ = 1，a₃ = 15，a₄ = 28．　 3分

(2) 由此猜想a_n = n (2n－1) ．　 4分

下面用数学归纳法加以证明：

①　　 当n = 1时，a₁ = 1×(2×1－1) = 1，结论正确；

当n = 2时，a₁ = 2×(2×2－1) = 6，结论正确．　 5分

②　　 假设n = k (k≥2)时结论正确，即a_k = k(2k－1) ．

则当n = k + 1时，∵ = k，

∴　　 (k－1)a_{k + 1} = (k + 1)a _k－(k + 1) = (k + 1)k(2k－1)－(k + 1)

= (k + 1)(2k²－k－1) = (k + 1)(2k + 1)(k－1)，

∵　　 k－1 ≠ 0，∴　　 a_{k + 1} = (k + 1)[2(k + 1)－1]，

即当n = k + 1时，结论正确．　　　　　　　　　　 7分

由①②可知，{a_n} 的通项公式是a_n = n (2n－1) ．　 8分

(3) ∵　　 　= 　= ( －)　 10分

∴　　 (+ + ┄ + ) = (1－) = ．　 12分

20、(本小题满分12分)

解：(1)设切去正方形边长为x，则焊接成的长方体的底面边长为4－2x，高为x，　 1分

所以V=(4－2x)²·x = 4(x³－4x² + 4x)　 (0<x<2) ．　　 3分

∴　　 V^/ = 4(3x²－8x + 4)，　　 4分

令V^/ = 0，即4(3x²－8x + 4) = 0，解得x₁ = ，x₂ = 2 (舍去) ．　 6分

又当x<时，V^/>0；当<x<2时，V^/<0．　　 7分

∴　　 当x = 时，V取得最大值V₁ = ．　 8分

(2)重新设计方案如下：

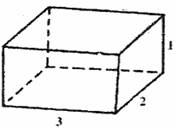
如图①，在正方形的两个角处各切下一个边长为1的小正方形；如图②，将切下的小正方形焊在未切口的正方形一边的中间；如图③，将图②焊成长方体容器.新焊长方体容器底面是一个长方形，长为3，宽为2，此长方体容积V₂ = 3×2×1 = 6，显然V₂>V₁．

故第二种方案符合要求．

　　　　　 图①　　　　　　　　　　　 图②　　　　　　　　　 　　　图③

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分

19、(本小题满分12分)

解：设z = a + bi (a,b Î R)，则z² = (a²－b²) + 2abi ，　 2分

　　 ∴　　 (a²－b²) + 2abi = 3 + 4i 　Û ，　 3分

　　 解得 或 ，　　 5分

　　 即z = 2 + i或z = －2－i ．　　　 6分

　　 又z³－6z + = 　= － ，　　 8分

　　 当z = 2 + i时，z³－6z + 　= －　= －+ i ；　 10分

　　 当z = －2 － i时，z³－6z + 　= －　= － i ．　 12分

18、(本小题满分12分)

解(1)从6个球中选取3个，共有A₆³种取法，　 2分

三次选取中，恰好有两次取到蓝色球，共有C₃¹C₄¹ A₂²种取法，　 4分

所以在三次选取中，恰好有两次取到蓝色球的概率为P = = ．　 6分

(2)设取球次数为随机变量x ，则x =1、2、3，　 8分

　　　 其分布列是：

　　　　　　　　　　　　　　　　　　　　　　　 10分

∴　 Ex =1×+ 2×+ 3×= 1.7．　　 12分

17、(本小题满分12分)

解：原不等式可化为(x－2)(x－a－1)≥0，　 2分

(1)　 当a + 1>2即a>1时，解得x≥a + 1或x≤2；　　 5分

(2)　 当a + 1 = 2即a = 1时，解得x Î R；　 7分

(3)　 当a + 1<2即a<1时，解得x≥2或x≤a + 1；　 10分

∴　　 原不等式的解集：当a≥1时，是；当a<1时，是

．

　　　　　　　　　　　　　　　　　　　　　　　　　　　　 12分