22．(本小题满分14分)

　　　　 已知曲线C的中心在原点，抛物线的焦点是双曲线C的一个焦点，且双曲

线C过点

　 (1)求双曲线C的方程；

　 (2)设双曲线C的实轴左顶点为A，右焦点为F，在第一象限内任取双曲线C上一点P，

　　　　 试问是否存在常数，使得恒成立？并证明你的结论.

河南省郑州三中2010届高中毕业班第二次质量预测题

21．(本小题满分12分)

已知a、b为实数，

　 (1)若上的极值；

　 (2)若上恒有的取值范围.

20．(本小题满分12分)

　　　　 已知x轴上有一点列：分有向线段所

成的比为，其中且为常数，

　 (1)证明是等比数列，并求数列的通项公式；

　 (2)设变化时，求的取值范围.

19．(本小题满分12分)

　　　　 已知长方体AC₁中，棱AB=BC=1，棱BB₁=2，连结B₁C过B点作B₁C的垂线交

CC₁于E，交B₁C于F.

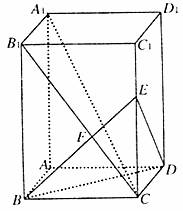　 (1)求证A₁C⊥平面EBD；

　 (2)求点A到平面A₁B₁C的距离；

　 (3)求平面A₁B₁CD与直线DE所成角的正弦值.

18．(本小题满分12分)

　　　　 有甲、乙两个盒子，甲盒子中有8张卡片，其中两张写有数字0，三张写有数字1，

三张写有数字2；乙盒子中有8张卡片，其中三张写有数字0，两张写有数字1，三张写

有数字2.

　 (1)如果从甲盒子中取两张卡片，从乙盒子中取一张卡片，那么取出的3张卡片都写有

1的概率是多少？

　 (2)如果从甲、乙两个盒子中各取一张卡片，设取出的两张卡片数字之和为，求的

分布列和期望值.

17．(本小题满分12分)

已知A、B、C的坐标分别为A(4，0)，B(0，4)，

　 (1)若的值；

　 (2)若的值.

16．在平面几何中有如下特性：从角的顶点出发的一条射线上任意一点到角两边的距离之比

为定值. 类比上述性质，请叙述在立体几何中相应的特性　　　　　　　　　 .

15．对任意两实数a、b、，定义运算“*”如下：

的值域为　　　　　　　　 .

14．一个总体中有100个个体，随机编号0，1，2，…，99，依从小到大的编号顺序平均分

成10个小组，组号依次为1，2，3，…，10. 现用系统抽样方法抽取一个容量为10的

样本，规定如果在第1组随机抽取的号码为m，那么在第k组中抽取的号码个位数字与

m+k的个位数字相同，若m=8，则在第8组中抽取的号码是　　　　　　　　　 .

13．i是虚数单位，的虚部为　　　　　　　 .