23. According to statistics, a man is more than twice as likely to die of skin cancer _________ a woman.

A. than　　　　 B. such　　　 C. so　　　　 D. as

22. Jane was asked a lot of questions, but she didn’t answer　 　　　　　of them.

A. other　　 B. any　　 C. none　　　　 D. some

第一节 单项选择(共15小题: 每小题1分, 共15分)

从每题所给的ABCD四个选项中, 选出可以填入空白处的最佳选项, 并在答题卡上将该项涂黑。

例: It is so nice to hear from her again. _____, we last met more than thirty years ago.

A. What’s more　 B. That’s to say　 C. In other words　 D. Believe it or not

答案是D。

21. The biggest whale is ___ blue whale, which grows to be about 29 meters long-the height of _____ 9-story building.

A. the; the　　　 B. a; a　　　 C. a; the　　 D. the; a

25．在平面直角坐标系中，抛物线与x轴交于A、B两点，(点A在点B左侧).与y轴交于点C，顶点为D，直线CD与x轴交于点E.

(1)请你画出此抛物线，并求A、B、C、D四点的坐标.

(2)将直线CD向左平移两个单位，与抛物线交于点F(不与A、B两点重合)，请你求出F点坐标.

(3)在点B、点F之间的抛物线上有一点P，使△PBF的面积最大，求此时P点坐标及△PBF的最大面积.

(4)若平行于x轴的直线与抛物线交于G、H两点，以GH为直径的圆与x轴相切，求该圆半径.

草　　 稿　　 纸

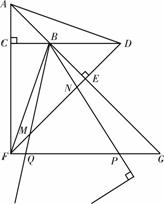
24．小华用两块不全等的等腰直角三角形的三角板摆放图形.

　　 (1)如图①所示△ABC，△DBE，两直角边交于点F，过点F作FG∥BC交AB于点G，连结BF、AD，则线段BF与线段AD的数量关系是　　　　　　 ；直线BF与直线AD的位置关系是　　　 　　 ，并求证：FG+DC＝AC；

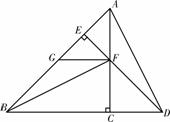
(2)如果小华将两块三角板△ABC，△DBE如图②所示摆放，使三点在一条直线上，AC、DE的延长线相交于点F，过点F作FG∥BC，交直线AE于点G，连结AD，FB，则FG、DC、AC之间满足的数量关系式是　　　　　 　　　　　；

(3)在(2)的条件下，若AG＝，DC＝5，将一个45°角的顶点与点B重合，并绕点B旋转，这个角的两边分别交线段FG于P、Q两点(如图③)，线段DF分别与线段BQ、BP相交于M、N两点，若PG＝2，求线段MN的长．

(第24题图①)　　　　　　 (第24题图②)

　　　　　　　　　　　　　　　　　　　　　　 (第24题图③)

23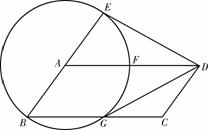．如图，平行四边形ABCD中，以A为圆心，AB为半径的圆交AD于F，交BC于G，延长BA交圆于E.

(1)若ED与⊙A相切，试判断GD与

⊙A的位置关系，并证明你的结论；

GC＝CD＝5，求AD的长.

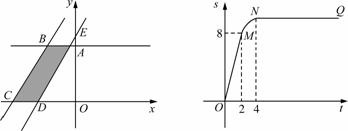
22．如图①所示，直角梯形OABC的顶点A、C分别在y轴正半轴与轴负半轴上.过点B、C作直线.将直线平移，平移后的直线与轴交于点D，与轴交于点E.

(1)将直线向右平移，设平移距离CD为(t≥0)，直角梯形OABC被直线扫过的面积(图中阴影部份)为，关于的函数图象如图②所示，OM为线段，MN为抛物线的一部分，NQ为射线，且NQ平行于x轴，N点横坐标为4，求梯形上底AB的长及直角梯形OABC的面积.

(2)当时，求S关于的函数解析式.

21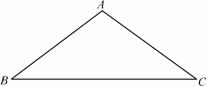．已知：如图，在中，，，将绕着点逆时针旋转后得到，点A落在点E处，点C落在点F处，连结.请你画出图形，并按下面要求完成本题.

(1)求证四边形是等腰梯形；