28．(本题满分12分)如图，抛物线的对称轴为直线x＝1，与x轴交于A、B两点，与y轴交于点C，其中A、C．

(1)求此抛物线的解析式；

(2)若此抛物线的顶点为P，将△BOC绕着它的顶点B顺时针在第一象限内旋转，旋转的角度为，旋转后的图形为△BO′C′．

①当O′C′ ∥CP时，求的大小；

　 ②△BOC在第一象限内旋转的过程中，当旋转后的△BO′C′有一边与BP重合时，求△BO′C′不在BP上的顶点的坐标．

27．(本题满分12分) 为了参观上海世博会，某公司安排甲、乙两车分别从相距300千米的上海、泰州两地同时出发相向而行，甲到泰州带客后立即返回，下图是它们离各自出发地的距离(千米)与行驶时间(小时)之间的函数图象．

(1)请直接写出甲离出发地的距离(千米)与行驶时间(小时)之间的函数关系式，并写出自变量的取值范围；

(2)当它们行驶4.5小时后离各自出发点的距离相等，求乙车离出发地的距离(千米)与行驶时间(小时)之间的函数关系式，并写出自变量的取值范围；

(3)在(2)的条件下，甲、乙两车从各自出发地驶出后经过多少时间相遇？

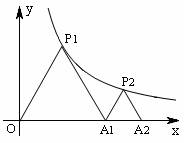
26．(本题满分10分)如图，P₁是反比例函数在第一象限图像上的一点，点A₁ 的坐标为(2，0)．

(1)当点P₁的横坐标逐渐增大时，△P₁O A₁的面积将如何变化？

(2)若△P₁O A₁与△P₂ A₁ A₂均为等边三角形，求此反比例函数的解析式及A₂点的坐标．

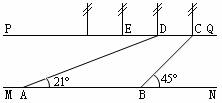
25．(本题满分10分)如图，泰州园博园中有一条人工河，河的两岸PQ、MN互相平行，河岸PQ上有一排间隔为50米的彩灯柱C、D、E、……，某人在河岸MN的A处测得∠DAN＝21º，然后沿河岸走了175米到达B处，测得∠CBN＝45º，求这条河的宽度．(参考数据：，)

24．(本题满分10分)如图，AB是⊙O的直径，C是BA延长线上的一点，CD与⊙O相切于点D，连接OD，四边形PQRS是矩形，其中点P、Q在半径OA上，点R在半径OD上，点S在⊙O上．已知CD=4，CO=5，PQ=2RQ，

(1)求的值；

(2)求矩形PQRS的面积．

23．(本题满分10分)有A、B两个口袋，A口袋中装有两个分别标有数字2，3的小球；B口袋中装有三个分别标有数字，4，的小球．小明先从A口袋中随机取出-个小球，用m表示所取球上的数字，再从B口袋中随机取出两个小球，用n表示所取球上的数字之和．

(1)用树状图法或列表法表示小明所取出的三个小球的所有可能结果；

(2)求的值是整数的概率．

22．(本题满分8分)如图，F为正方形ABCD的对角线AC上一点，FE⊥AD于点E，M为CF的中点．

(1)求证：MB=MD；

(2)求证：ME=MB．

21．(本题满分8分)对某校学生会倡导的“献爱心，送温暖”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据．下图是根据这组数据绘制的统计图，图中从左到右各矩形的高度之比为3：4：5：8：6，又知此次调查中捐款10元和30元的学生一共27人．

(1)这次抽样一共调查了多少学生？这组捐款数据的中位数是多少？

(2)若该校共有1560名学生，请估算全校学生共捐款多少元？