3．考查复数的概念及集合的运算，容易题．，则中的复数必须为实数，所以m=-2；实部恰为8．提醒学生在解决复数问题时，主要手段为对实、虚部的实数化计算．

2．考查充要条件及立几中直线与平面垂直的判定及性质，考查学生的空间想象能力和逻辑推理能力，容易题．讲评时可提醒学生解此类立几问题时要有构建模型举反例的意识．

1．考查统计中总体分布的估计，容易题．考前要提醒学生注意回顾相关知识，不能造成考试中知识的盲点．

4．(本题满分10分)

已知，

(其中)

⑴求及；

⑵试比较与的大小，并说明理由．

3．(本题满分10分)

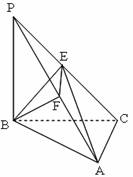
如图，三棱锥中，底面于，，点分别是的中点，求二面角的余弦值．

2．(本题满分10分)

已知曲线，直线．

⑴将直线的极坐标方程化为直角坐标方程；

⑵设点在曲线上，求点到直线距离的最小值．

(总分40分，加试时间30分钟)

答卷前，请考生务必将自己的学校、姓名、考试号等信息填写在答卷密封线内．解答过程应写在答题卷的相应位置上，在其它地方答题无效。

1．(本题满分10分)

已知在一个二阶矩阵对应变换的作用下，点变成了点，点变成了点，求矩阵．

20．(本题满分16分)

已知函数，，，其中，且.

⑴当时，求函数的最大值；

⑵求函数的单调区间；

⑶设函数若对任意给定的非零实数，存在非零实数()，

使得成立，求实数的取值范围.

[扬州市教育科学研究院命制]

高三数学试卷　 第4页(共4页)

　 扬州市2009~2010学年度第一学期期末高考模拟考试

19．(本小题满分16分)

已知数列，.

⑴求证：数列为等比数列；

⑵数列中，是否存在连续的三项，这三项构成等比数列？试说明理由；

⑶设，其中为常数，且，

，求.

18. (本题满分15分)

已知圆，点，直线.

⑴求与圆相切，且与直线垂直的直线方程；

⑵在直线上(为坐标原点)，存在定点(不同于点)，

满足：对于圆上任一点，都有为一常数，试求所有

满足条件的点的坐标.