18． 解：(1)已知点在半圆上，

所以，又，所以，　 (2分)

当半圆在点处的切线与直线平行时，点到直线的距离最大，此时的面积取得最大值，

故半圆在点处的切线与直线平行，

所以，又，

所以，又，所以，(4分)

所以曲线的方程为或。　 (6分)

(2)点，点，设，则有

直线的方程为，

令，得，　 所以；　　　 (9分)

直线的方程为，

令，得，　　 所以；　　 (11分)

则，

又由，得，代入上式得

，所以为定值(15分)

17.解：(1)由题意有，设，则有，从而可得．

而，因此，从而．　 ………………6分

(2)　 由(1)得： ，于是，，即.………………9分

另一方面，对于任意实数，存在初始值，使得．13分

所以的取值集合为．　　　　　　　 ………………15分

16. 解：(Ⅰ)证明：侧面，

侧面，，　　　　　　　 ………3分

在中，，则有，　

，，　　　　　 ………………………………………6分

又平面．　　　　 ……………………………………7分

(Ⅱ)证明：连、，连交于，

，，四边形是平行四边形，……………10分

　　　　 　　　　　　　　　　　　　　　………………………11分

又平面，平面，平面．　 ………14分

15. 解：(1)：，

　……………………5分

 (定值)　　　　 　………………8分

(2)由(1)可知A、B为锐角

所以的最大值为，此时三角形ABC为钝角三角形。…………………14分

20. 已知集合M是满足下列性质的函数f(x)的全体：存在非零常数T，对任意x∈R，有f(x+T)=T f(x)成立.

(1)函数f(x)= x 是否属于集合M？说明理由；　

(2)设函数f(x)=a^x(a>0,且a≠1)的图象与y=x的图象有公共点，证明： f(x)=a^x∈M；

　(3)若函数f(x)=sinkx∈M ,求实数k的取值范围.

　　　　　　　　　　　　　　 高三数学试卷　 第4页 (共4页)

扬州市2010届高三第二次高考模拟考试样卷(一)

　 评分标准及评分建议(正题)

19.　 A地产汽油，B地需要汽油．运输工具沿直线AB从A地到B地运油，往返A，B一趟所需的油耗等于从A地运出总油量的．如果在线段AB之间的某地C(不与A，B重合)建一油库，则可选择C作为中转站，即可由这种运输工具先将油从A地运到C地，然后再由同样的运输工具将油从C地运到B地．设＝x，往返A，C一趟所需的油耗等于从A地运出总油量的．往返C，B一趟所需的油耗等于从C地运出总油量的．不计装卸中的损耗，定义：运油率P＝，设从A地直接运油到B地的运油率为P₁，从A地经过C中转再运油到B地的运油率为P₂．

(1)比较P₁，P₂的大小；　　　　　　　　　

(2)当C地选在何处时，运油率P₂最大？

18.已知半椭圆和半圆组成曲线，其中；如图，半椭圆内切于矩形，且交轴于点，点是半圆上异于的任意一点，当点位于点时，的面积最大。　

(1)求曲线的方程；　　

(2)连、交分别于点，

求证：为定值。

　　　　　　　　　　　　　　 高三数学试卷　 第3页 (共4页)

17. 　实数列满足．问：

(1)如果，求；

(2)求的取值构成的集合

16.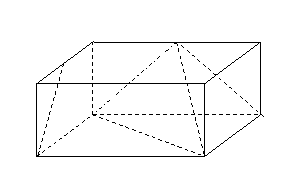 如图，在长方体中，，，、分别为、的中点．

(Ⅰ)求证：平面；　　

(Ⅱ)求证：平面．

15.已知是△ABC的两个内角，

(其中是互相垂直的单位向量)，若。　　 　

(1)试问是否为定值，若是定值，请求出，否则说明理由；

(2)求的最大值，并判断此时三角形的形状。

　　　　　　　　　　　　　　 高三数学试卷　 第2页 (共4页)