2．“物理实验类比法”探究题

类比是物理思维的基本方法，它是一种推理。类比推理是根据两个(或两类)对象在某些属性或关系上相似而推出它们在另一个属性或关系上也可能相似的一种推理形式。巧用类比法把抽象的物理问题化难为易，可以给我们的解题带来方便。

例3．(2008年四川卷)图为“双棱镜干涉”实验装置，其中为单色光源，为一个顶角略小于的等腰三角形棱镜，为光屏。位于棱镜对称轴上，屏与棱镜底边平行。调节光路，可在屏上观察到干涉条纹。这是由于光源发出的光经棱镜作用后，相当于在没有棱镜时，两个分别位于图中和位置的相干波源所发出的光的叠加。(和的连线与棱镜底边平行)

已知和的位置可由其它实验方法确定，类比“双缝干涉测波长”的实验，可以推测出若要利用“双棱镜干涉”测量光源发出的单色光的波长时，需要测量的物理量是：　　　　　　　 ，　　　　　　　　 和　　　　　　　　 。

答案：与间的距离，(或)与光屏间的距离，干涉条纹间距。

解析：由杨氏双缝干涉实验可知，只有相干光源发出的光互相叠加时，才能产生干涉现象。“双棱镜干涉”也能在屏上观察到干涉条纹，这就是说它肯定有相干光源。正如题干所说由于光源发出的光经棱镜作用后，相当于在没有棱镜时，两个分别位于图中和位置的相干波源所发出的光的叠加。在两光束相交的区域放置观察屏，在、区间就可以观察到干涉条纹。那么和就相当于杨氏实验中的双缝，所以两虚光源与间距离就相当于杨氏实验公式中的，(或)与光屏间的距离就相当于公式中的。于是，自然得出双棱镜中的。测量光源发出的单色光的波长只需将公式变形为。

例4.(2005年江苏高考题)1801年，托马斯·杨用双缝干涉实验研究了光波的性质。1834年，洛埃利用单面镜同样得到了杨氏干涉的结果(称洛埃镜实验)。

(1)洛埃镜实验的基本装置如图所示，为单色光源，为一平面镜。试用平面镜成像作图法在答题卡上画出经平面镜反射后的光与直接发出的光在光屏上相交的区域。

(2)设光源到平面镜的垂直距离和到光屏的垂直距离分别为和,光的波长为，在光屏上形成干涉条纹。写出相邻两条亮纹(或暗纹)间距离的表达式。

洛埃镜实验也能演示干涉现象，那么它肯定有相干光波源。光源由平面镜反射后的光线可以视为虚光源发出的光线，直接传播光和反射光是相干光。物点及其像点就相当于杨氏实验中的双缝，与间距离就相当于杨氏实验公式中的，(或)与光屏间的距离就相当于公式中的。于是，自然得出洛埃镜中的的公式。

1．“物理公式合理性”探究题

一个物理公式总是有使用条件的，在使用它之前，一定要先搞清楚所要处理的问题是否满足该条件，切不可拿来就用。①得到一个公式之后，若要判断其对错，最简单的方法之一是看等式两端的单位是否一致。②一个公式在物理上是否合理也是至关重要的，通常的判别方法是，看它在特殊或极端情况下能否成立。

例1．(09年北京理综)图为一个内、外半径分别为和的圆环状均匀带电平面，其单位面积带电量为。取环面中心为原点，以垂直于环面的轴线为轴。设轴上任意点到点的距离为，点电场强度的大小为。下面给出的四个表达式(式中为静电力常量)，其中只有一个是合理的。你可能不会求解此处的场强，但是你可以通过一定的物理分析，对下列表达式的合理性做出判断。根据你的判断，的合理表达式应为(　　 )

A．　　 B．

C．　　　 D．

解析：根据原则①我们能首先排除选项A。因为它的单位是，而的单位是。根据原则②我们能排除选项C和D。因为圆环电荷是对称分布的，所以圆心处的场强。我们可以取一些特殊的点，令，而此时选项C中的场强。我们在极端情况下用极限的思维方式去思考，如果，那么所求场强应该是，而此时选项D中的场强。故选项B正确。

例2．(08年北京理综)有一些问题你可能不会求解，但是你仍有可能对这些问题的解是否合理进行分析和判断。例如从解的物理量单位，解随某些已知量变化的趋势，解在一些特殊条件下的结果等方面进行分析，并与预期结果、实验结论等进行比较，从而判断解的合理性或正确性。

举例如下：如图所示。质量为倾角为的滑块放于水平地面上。把质量为的滑块放在的斜面上。忽略一切摩擦，有人求得相对地面的加速度,式中为重力加速度。

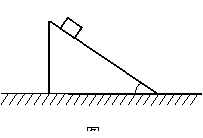
对于上述解，某同学首先分析了等号右侧量的单位，没发现问题。他进一步利用特殊条件对该解做了如下四项分析和判断，所得结论都是“解可能是对的”。但是，其中有一项是错误的。请你指出该项。(　　 )

A.当时，该解给出，这符合常识，说明该解可能是对的

B.当时，该解给出,这符合实验结论，说明该解可能是对的

C.当时，该解给出,这符合预期的结果，说明该解可能是对的

D.当时，该解给出,这符合预期的结果，说明该解可能是对的

解析：正如题干所述，根据原则①某同学首先分析了等号右侧量的单位，没发现问题。根据原则②一个公式在物理上是否合理也是至关重要的，通常的判别方法是，看它在特殊或极端情况下能否成立。选项A、B分别取了和这两类特殊情况，所以都是正确的。接着我们在极端情况下用极限的思维方式去思考，当时，。而当时，

。所以选项C正确，选项D的分析是错误的。

那么相对地面的加速度是如何求出来的呢？它的解法如下：

设滑块的加速度为，滑块的加速度为。以滑块、为系统研究，水平方向上系统不受外力，动量守恒，取向右的方向为正方向，有：

将上式对时间求一阶导数，得：　　 　　　　　　　　　　　　　①

对滑块分析，如图所示

在上下滑，以为参照物，则受到一个惯性力(方向与加速度方向相反)。所以相对下滑。由牛顿第二定律有：

因为：

所以水平方向和竖直方向的绝对加速度由上式可知：

　 　②

　　　　　　　　　　　　　　　　　　 　③

联立①②③式，得：

所以，相对地面的加速度为：

22.数列：满足

(1)　 设，求证是等比数列；

(2)　 求数列的通项公式；

(3)　 设,数列的前项和为，求证：

21．已知双曲线中心在原点，焦点在x轴上，实轴长为2。一条斜率为1的直线经过双曲线的右焦点与双曲线相交于A、B两点，以AB为直径的圆与双曲线的右准线相交于M、N。

　 (1)若双曲线的离心率2，求圆的半径；

　 (2)设AB中点为H，若，求双曲线方程。

20.如图，在四棱锥P-ABCD中，底面ABCD是矩形，已知AB = 3，AD = 2，PA = 2，，．

(1)　 证明：AD⊥平面PAB；

(2)　 求异面直线PC与AD所成的角的大小；

(3)　 求二面角P-BD-A的大小．

19.已知函数的导数．a，b为实数，．

(1)　 若在区间上的最小值、最大值分别为、1，求a、b的值；

(2)　 在 (1) 的条件下，求曲线在点P(2，1)处的切线方程．

18.有A、B、C、D、E共5个口袋，每个口袋装有大小和质量均相同的4个红球和2个黑球，现每次从其中一个口袋中摸出3个球，规定：若摸出的3个球恰为2个红球和1个黑球，则称为最佳摸球组合．

(1)　 求从口袋A中摸出的3个球为最佳摸球组合的概率；

(2)　 现从每个口袋中摸出3个球，求恰有3个口袋中摸出的球是最佳摸球组合的概率．

17．已知的周长为

　 (1)求边AB的长；

　 (2)若的面积，求角C的大小。

16. 给出下列命题：

①．函数和的图象关于直线对称.

②．在上连续的函数若是增函数，则对任意均有成立.

③．已知函数的交点的横坐标为的值为.

④．底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥.

⑤．若为双曲线上一点，、分别为双曲线的左右焦点，且，则或_.

其中正确的命题是　　　　　　 (把所有正确的命题的选项都填上)

15.某旅馆有三人间、两人间、单人间三种房间各一间可用，有三个成人带两个小孩来投宿，小孩不宜单住一间(必须有成人陪同)．若三间房都住有人，则不同的安排住宿方法有________种．