
2.下列关于溶酶体的说法不正确的是
A.小蝌蚪的尾巴最终消失,其中起作用的是溶酶体
B.溶酶体内含有多种水解酶,能够分解多种物质,是细胞的“消化车间”
C.溶酶体能分解衰老、损伤的细胞器,吞噬并杀死入侵的病毒或病菌,有一定的防御作用
D.刚宰杀的禽、畜放置一段时间再煮口味会更好,其原因为溶酶体和线粒体的共同作用释放出更丰富的营养物质的缘故
1.下列各项中,基本单位完全相同一的项是
A.质粒,基因,染色体 B.糖原,纤维蛋白原,抗原
C.脂肪,胆固醇,维生素D D.胰岛素,生长激素,抗体
22.解(1)由x2=4y得y= x2, y′=
x2, y′= x. ∴直线l的斜率为y′|x=2=1.
x. ∴直线l的斜率为y′|x=2=1.
故l的方程为y=x-1,∴点A坐标为(1,0). ----------------------------------------------4`
(2) 设M(x,y),则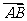 =(1,0),
=(1,0), =(x-2,y),
=(x-2,y),  =(x- 1,y),由
=(x- 1,y),由 =0得(x-2)+y·0+
=0得(x-2)+y·0+ 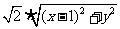 =0, 整理,得
=0, 整理,得  +y2 =1.轨迹K是椭圆。---9`
+y2 =1.轨迹K是椭圆。---9`
设
从而得
因为E、F 都在椭圆上,所以满足椭圆方程:
消去 ,并整理得
,并整理得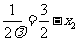 ①-------------------------------------------11`
①-------------------------------------------11`
由题意,设过点B的直线方程: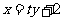 ,
,
当直线与椭圆相切时,
即 , 取
, 取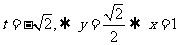 得切点(1,
得切点(1, )
)
所以知
联系①式知,
即ΔOBE与ΔOBF面积之比的取值范围是 。-----------15`
。-----------15`

21.
 ---------------------------------------------2`
---------------------------------------------2`
(1)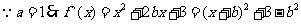 ,
,
 的导函数的图象关于直线x=2对称
的导函数的图象关于直线x=2对称 --------------------4`
--------------------4`
 |
(0,1) |
1 |
(1,3) |
3 |
 |
+ |
0 |
- |
0 |
 |
递增 |
|
递减 |
|
 在区间[0,2]上的最小值=min{
在区间[0,2]上的最小值=min{ 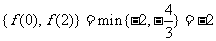 ------7`
------7`
(2) 由 ,且
,且 在区间
在区间 上单调递增,知:
上单调递增,知: 恒成立
恒成立

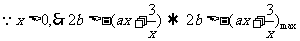 -----------------------10`
-----------------------10`
为求最大值,先以下求函数 的最小值
的最小值
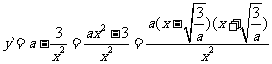
当 时,
时, 在
在 上为负,在
上为负,在 为正,
为正,
即 在
在 上递减,在
上递减,在 递增
递增
 的最小值是
的最小值是
当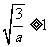 时,
时, 在区间
在区间 上恒为负,即
上恒为负,即 在区间
在区间 上单调递减,所以
上单调递减,所以 的最小值是
的最小值是 -----------------------------------------13`
-----------------------------------------13`
经检验,以上端点值也符合。
综上所述,当 时,
时, 的取值范围是
的取值范围是
当 时
时 的取值范围是
的取值范围是 ---------------15`
---------------15`
20.(I)当 时,
时,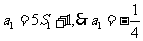


又
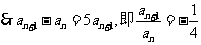 且
且
∴数列 是首项为
是首项为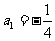 ,公比为
,公比为 的等比数列,
的等比数列,
∴ ,-----------------------7`
,-----------------------7`
(2)


又 
当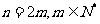 (偶数)时,比值=
(偶数)时,比值=
当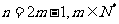 (奇数)时,比值=
(奇数)时,比值= 关于m为递增数列,当m=1时,取到最小值
关于m为递增数列,当m=1时,取到最小值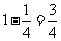
综上所述,对任何正整数n,不等式 恒成立。--------14`
恒成立。--------14`
19.证明:在正方形ABDE中,EA⊥AB,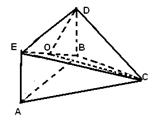
又 AB= 平面ABDE∩平面ABC,平面ABDE⊥平面ABC
所以,EA⊥平面ABC,-----------------------------------------------4`
又 EA在平面ACE内,所以,平面ACE⊥平面ABC。---------7`
(2)同理,由AB⊥BC可知:BC⊥平面ABDE,进而知,BC⊥AD
在正方形ABDE中,AD⊥BE,又 BC∩BE=B,知 AD⊥平面BCE。-------10`
设BE∩AD=O,连结OC,则CD与平面BCE所成的角就是∠DCO,且DO⊥CO---12`
在正方形ABDE中,由AB=1知,DO= ,
,
在直角三角形CDO中,依前知,sin∠DCO= ,
,
即CD与平面BCE所成角的正弦值是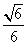 ---------------------------14`
---------------------------14`
18.解: , 所以
, 所以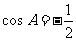 ,又因为A是三角形的内角,即
,又因为A是三角形的内角,即 ---------7`
---------7`



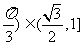 -------10`---12`
-------10`---12`
又  ,即
,即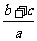 的取值范围是
的取值范围是 ---------------14`
---------------14`
22.(本题15分)已知直线L与抛物线C: 相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B(2,0)
相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B(2,0)
(1) 求点A的横坐标。
(2)设动点M满足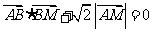 ,点M的轨迹K。若过点B的直线L1(斜率不等于0)与轨迹K交于不同的两点E、F(E在B、F之间),试求ΔOBE与ΔOBF面积之比的取值范围。
,点M的轨迹K。若过点B的直线L1(斜率不等于0)与轨迹K交于不同的两点E、F(E在B、F之间),试求ΔOBE与ΔOBF面积之比的取值范围。
21.(本题15分)已知函数 ,其中
,其中
(1) 若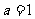 ,且
,且 的导函数的图象关于直线x=2对称时.试求
的导函数的图象关于直线x=2对称时.试求 在区间[0,2]上的最小值。
在区间[0,2]上的最小值。
(2) 若 ,且
,且 在区间
在区间 上单调递增,试用
上单调递增,试用 表示出
表示出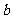 的取值范围.
的取值范围.
20.(本题14分)设数列 的前
的前 项和为
项和为 ,对任意的正整数
,对任意的正整数 ,都有
,都有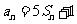 成立。(1)求数列
成立。(1)求数列 的通项公式;
的通项公式;
(2)求证:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com