
1.(1)21世纪是城市发展的重要时期。(2)对未来城市生活的憧憬与展望是一项全球性课题。(2分)
3.(本题满分16分)已知函数 其中n∈N*,a为常数.
其中n∈N*,a为常数.
(Ⅰ)当n=2时,求函数f(x)的极值;
(Ⅱ)当a=1时,若 均非负数,且
均非负数,且 ,求证:
,求证:
 .(自编)
.(自编)
提示:(Ⅰ)由已知得函数f(x)的定义域为{x|x>-1},
当n=2时,
所以 
(1)当a>0时,由 得
得
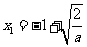 >-1,
>-1, <-1,
<-1,
此时 f′(x)= .
.
当x∈(1,x1)时,f′(x)<0,f(x)单调递减;
当x∈(x1+∞)时,f′(x)>0, f(x)单调递增.
(2)当a≤0时,f′(x)<0恒成立,所以f(x)无极值.
综上所述,n=2时,
当a>0时,f(x)在 处取得极小值,极小值为
处取得极小值,极小值为
当a≤0时,f(x)无极值.
(Ⅱ)先证明当 只要设
只要设
 ,
,

而 均非负数, 且
均非负数, 且 ,所以
,所以
点评:该题考查导数运算、解二次不等式、研究函数单调性及极值、分类讨论思想、导数应用、灵活的运用所学知识处理问题得能力.是难题.
2.
(本题满分16分)已知数列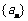 中,
中, ,对于任意的
,对于任意的 ,有
,有
(1)求数列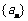 的通项公式;
的通项公式;
(2)若数列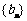 满足:
满足: 求数列
求数列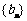 的通项公式;
的通项公式;
(3)设 ,是否存在实数
,是否存在实数 ,当
,当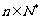 时,
时,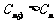 恒成立,若存在,求实数
恒成立,若存在,求实数 的取值范围,若不存在,请说明理由.(自编)
的取值范围,若不存在,请说明理由.(自编)
提示:(1)取p=n,q=1,则
∴ (
(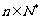 )
)
∴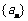 是公差为2,首项为2的等差数列
是公差为2,首项为2的等差数列
∴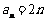 …………………………………………(4分)
…………………………………………(4分)
(2)∵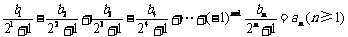 ①
①
∴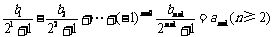 ②
②
①-②得:

当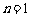 时,
时,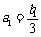 ∴
∴ 满足上式
满足上式
∴ ……………………………(9分)
……………………………(9分)
(3)
假设存在 ,使
,使



当 为正偶函数时,
为正偶函数时, 恒成立
恒成立

当 时
时
∴
当 为正奇数时,
为正奇数时, 恒成立
恒成立
∴
当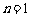 时
时
∴
综上,存在实数 ,且
,且 ……………………………………(16分)
……………………………………(16分)
点评:该题考查等差数列、等比数列、和与通项关系、函数性质、分类讨论思想、不等式性质以及综合运用能力;是难题.
1.(本题满分16分) 已知:以点C (t,
)(t∈R
, t ≠ 0)为圆心的圆与 轴交于点O, A,与y轴交于点O, B,其中O为原点.
轴交于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线y = –2x+4与圆C交于点M, N,若OM = ON,求圆C的方程.(自编)
解 (1) ,
, .
.
设圆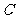 的方程是
的方程是 
令 ,得
,得 ;令
;令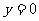 ,得
,得
 ,即:
,即: 的面积为定值.……6分
的面积为定值.……6分
(2)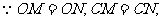
 垂直平分线段
垂直平分线段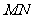 .
.
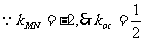 ,
, 直线
直线 的方程是
的方程是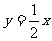 .
.
 ,解得:
,解得:
当 时,圆心
时,圆心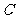 的坐标为
的坐标为 ,
, ,
,
此时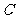 到直线
到直线 的距离
的距离 ,
,
圆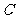 与直线
与直线 相交于两点.
相交于两点.
当 时,圆心
时,圆心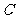 的坐标为
的坐标为 ,
, ,
,
此时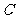 到直线
到直线 的距离
的距离
圆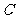 与直线
与直线 不相交,
不相交, 不符合题意舍去.
不符合题意舍去.
 圆
圆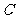 的方程为
的方程为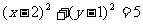 .……………………………………16分
.……………………………………16分
点评:该题考查两点间距离公式、圆的标准方程、直线的斜率与方程、直线与圆的为之关系以及分类讨论的思想.是中档题.
20.(本小题满分16分)
已知在数列 中,
中, ,且点
,且点 在直线
在直线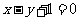 上.
上.
(1)求数列 的通项公式;
的通项公式;
(2)若函数
 ,
,
求函数 的最小值;
的最小值;
(3)若 表示数列
表示数列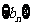 的前
的前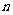 项和,试问:是否存在关于
项和,试问:是否存在关于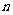 的整式
的整式 ,使得
,使得
 对一切
对一切 的自然数
的自然数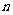 恒成立?若存在,写出
恒成立?若存在,写出 的
的
解析式并证明,若不存在,请说明理由.
江苏省梁丰高级中学2009-2010学年度第二学期期中考试
19.(本小题满分16分)
为了研究某种药物,用小白鼠进行试验,发现药物在血液内的浓度与时间的关系因使用方式的不同而不同.若使用注射方式给药,则在注射后的3小时内,药物在白鼠血液内的浓度 与时间
与时间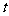 满足关系式:
满足关系式: ,若使用口服方式给药,则药物在白鼠血液内的浓度
,若使用口服方式给药,则药物在白鼠血液内的浓度 与时间
与时间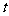 满足关系式:
满足关系式: .现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰.
.现对小白鼠同时进行注射和口服该种药物,且注射药物和口服药物的吸收与代谢互不干扰.
(1)若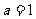 ,求3小时内,该小白鼠何时血液中药物的浓度最高,并求出最大值;
,求3小时内,该小白鼠何时血液中药物的浓度最高,并求出最大值;
(2)若使小白鼠在用药后3小时内血液中的药物浓度不低于4,求正数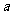 的取值范围.
的取值范围.
18.(本小题满分15分)
已知集合 ,
,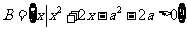 .
.
(1)当 时,求
时,求 ;
;
(2)若 ,求实数
,求实数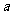 的取值范围.
的取值范围.
17.(本小题满分15分)
已知等差数列{an}中,首项a1=1,公差d为整数,且满足a1+3<a3,a2+5>a4,数列{bn}满足 ,其前n项和为Sn.
,其前n项和为Sn.
(1)求数列{an}的通项公式an;
(2)若S2为S1,Sm(m∈N*)的等比中项,求m的值.
16.(本小题满分14分)
已知函数 .
.
(1) 若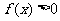 ,求实数
,求实数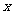 的取值范围;
的取值范围;
(2)判断函数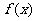 的单调性,并用函数单调性的定义加以证明;
的单调性,并用函数单调性的定义加以证明;
(3)判断函数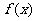 的奇偶性,并说明理由.
的奇偶性,并说明理由.
15.(本小题满分14分)
在 中,角
中,角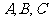 的对边分别是
的对边分别是 .
. 为锐角,
为锐角,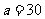 ,
, 的面积
的面积
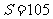 ,外接圆半径
,外接圆半径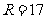 .
.
(1)求 的值;
的值;
(2)求 的周长.
的周长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com